剑指offer编程题66道题 26-35
26.二叉搜索树与双向链表
题目描述
输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。
中序遍历思路：
按照右中左的顺序，中序遍历对节点的访问顺序和转换完链表从左到右的顺序是一样的。所以在中序遍历时完成相邻两个节点的互指即可。
具体做法是把前一个节点记录下来然后pre->right=cur;cur->left=pre。
/** public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } */ public class Solution { TreeNode pre = null; public TreeNode Convert(TreeNode pRootOfTree) { if(pRootOfTree == null) return pRootOfTree; Convert(pRootOfTree.right); if(pre == null){ pre = pRootOfTree; } else { pre.left = pRootOfTree; pRootOfTree.right = pre; pre = pRootOfTree; } Convert(pRootOfTree.left); return pre; } }
最开始我采用的是这种解法，有两个问题：
1.采用左中右的中序遍历，遍历完之后头结点还得从右到左挪回来
2.更严重的问题是，我将pre设置为局部传递的变量，由于pre是引用的值传递，在递归回退的时候，pre的引用时上一次遍历pre的副本，而不是遍历后更改的值。解决方法就是讲pre设置为全局变量。
切记！！！java只有值传递！只有值传递！只有值传递！
对于基本类型，java都是传值。而对于引用类型，其实java也是通过值传递的，只是传递的值不是实例本身，而是实例的引用的副本。
参考java的传值与传引用
错误解法：
/** public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } */ public class Solution { public TreeNode Convert(TreeNode pRootOfTree) { if(pRootOfTree == null) return null; TreeNode pre = null; ConvertHelper(pRootOfTree,pre); TreeNode res = pRootOfTree; while(res.left != null){ res = res.left; } return res; } public void ConvertHelper(TreeNode cur, TreeNode pre){ if(cur == null) return; ConvertHelper(cur.left,pre); cur.left = pre; if(pre!=null) pre.right = cur; pre = cur; ConvertHelper(cur.right,pre); } }
非递归实现：
链接：https://www.nowcoder.com/questionTerminal/947f6eb80d944a84850b0538bf0ec3a5 来源：牛客网 import java.util.Stack; public class Solution { public TreeNode Convert(TreeNode pRootOfTree) { if(pRootOfTree == null) return pRootOfTree; TreeNode list = null; Stack<TreeNode> s = new Stack<>(); while(pRootOfTree != null || !s.isEmpty()){ if(pRootOfTree != null) { s.push(pRootOfTree); pRootOfTree = pRootOfTree.right; } else { pRootOfTree = s.pop(); if(list == null) list = pRootOfTree; else { list.left = pRootOfTree; pRootOfTree.right = list; list = pRootOfTree; } pRootOfTree = pRootOfTree.left; } } return list; } }
27.字符串的排列
题目描述
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
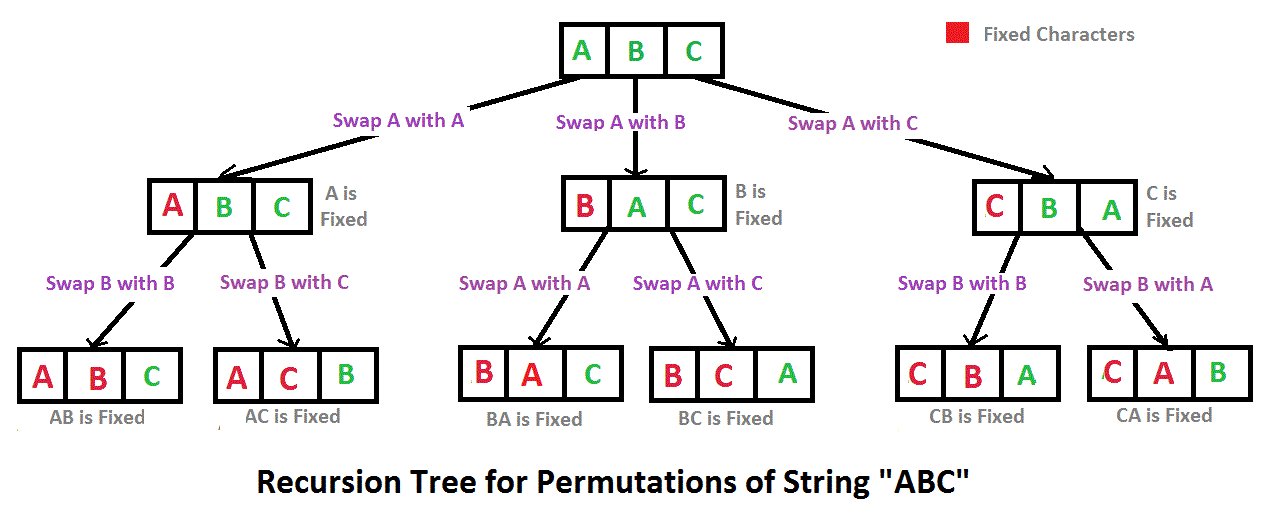
import java.util.ArrayList; import java.util.Collections; public class Solution { public ArrayList<String> Permutation(String str) { ArrayList<String> list = new ArrayList<String>(); if(str !=null && str.length() > 0){ PermutationHelper(str.toCharArray(),0,list); Collections.sort(list); } return list; } public void PermutationHelper(char[] cs, int i, ArrayList<String> list){ if(cs.length-1 == i){ String val = String.valueOf(cs); if(!list.contains(val)){ list.add(val); } }else{ for(int j=i; j<cs.length;j++){ swap(i,j,cs); PermutationHelper(cs,i+1,list); swap(i,j,cs); } } } public void swap(int i,int j,char[] cs){ char temp = cs[i]; cs[i] = cs[j]; cs[j] = temp; } }
最后一个循环是递归调用swap交换前后两个字符，在最后交换完成入List之后再交换回来，回到初始状态再进下一个循环
28.数组中出现次数超过一半的数字
题目描述
数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。
例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。
第一种普通解法：耗时10ms
import java.util.*; public class Solution { public int MoreThanHalfNum_Solution(int [] array) { Map<Integer,Integer> count = new HashMap<>(); if(array.length == 1) return array[0]; for(int i:array){ if(!count.containsKey(i)){ count.put(i, 1); }else{ count.put(i,count.get(i)+1); if(count.get(i) > array.length/2) return i; } } return 0; } }
第二种解法：耗时10ms
采用阵地攻守的思想：
第一个数字作为第一个士兵，守阵地；count = 1；
遇到相同元素，count++;
遇到不相同元素，即为敌人，同归于尽,count--；当遇到count为0的情况，又以新的i值作为守阵地的士兵，继续下去，到最后还留在阵地上的士兵，有可能是主元素。
再加一次循环，记录这个士兵的个数看是否大于数组一般即可。
public class Solution { public int MoreThanHalfNum_Solution(int [] array) { if(array.length == 1) return array[0]; int result = array[0]; int times = 0; for(int i = 0;i<array.length; i++){ if(times == 0){ result = array[i]; times = 1; }else if(result == array[i]){ times++; }else{ times--; } } times=0; for(int i=0;i<array.length;i++){ if(result==array[i]){ times++; } } if(times*2<=array.length){ result=0; } return result; } }
29.最小的K的个数
题目描述
输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4,。
1.偷懒解法（利用jdk自带的排序api）：
import java.util.*; public class Solution { public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) { ArrayList<Integer> list = new ArrayList<>(); if(k>input.length) return list; Arrays.sort(input); for(int i:Arrays.copyOfRange(input, 0, k)){ list.add(i); } return list; } }
2.创建一个大小为k的数据容器，如果容器还没有有了k个数字，直接放入这个数到容器当中；如果容器中有了k个数字了，找出这已有的k个数字中的最大值，然后拿待插的数和最大值进行比较，小就替换，大就抛弃。如果用二叉树来实现这个容器，那么我们可以在O(logk)实现查找替换操作，对于n个输入数字而言，总的时间效率为O(nlogk)。
import java.util.ArrayList; import java.util.PriorityQueue; import java.util.Comparator; public class Solution { public ArrayList<Integer> GetLeastNumbers_Solution(int[] input, int k) { ArrayList<Integer> result = new ArrayList<Integer>(); int length = input.length; if(k > length || k == 0){ return result; } PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(k, new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o2.compareTo(o1); } }); for (int i = 0; i < length; i++) { if (maxHeap.size() != k) { maxHeap.offer(input[i]); } else if (maxHeap.peek() > input[i]) { Integer temp = maxHeap.poll(); temp = null; maxHeap.offer(input[i]); } } for (Integer integer : maxHeap) { result.add(integer); } return result; } }
最大堆直接只用了PriorityQueue实现，它的默认实现是最小堆，改变他的排序方式就可以实现最大堆。
PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(k, new Comparator<Integer>() { @Override public int compare(Integer o1, Integer o2) { return o2.compareTo(o1); } });
3.冒泡法
这种方法比较简单，就是时间复杂度为O(n*k)，稍高
链接：https://www.nowcoder.com/questionTerminal/6a296eb82cf844ca8539b57c23e6e9bf 来源：牛客网 public ArrayList<Integer> GetLeastNumbers_Solution(int [] input, int k) { ArrayList<Integer> al = new ArrayList<Integer>(); if (k > input.length) { return al; } for (int i = 0; i < k; i++) { for (int j = 0; j < input.length - i - 1; j++) { if (input[j] < input[j + 1]) { int temp = input[j]; input[j] = input[j + 1]; input[j + 1] = temp; } } al.add(input[input.length - i - 1]); } return al; }
30.连续子数组的最大和
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。你会不会被他忽悠住？(子向量的长度至少是1)
1.两个循环遍历，时间复杂度为O（n2）
public class Solution { public int FindGreatestSumOfSubArray(int[] array) { double max = -1.0/0.0; for(int i = 0;i<array.length;i++){ double submax = -1.0/0.0; int sum = 0; for (int j=i;j<array.length;j++){ sum = sum + array[j]; if(sum > submax) submax = sum; } if(submax>max) max = submax; } return (int)max; } }
public class Solution { public int FindGreatestSumOfSubArray(int[] array) { int max = array[0]; for(int i = 0;i<array.length;i++){ int submax = array[i]; int sum = array[i]; for (int j=i+1;j<array.length;j++){ sum = sum + array[j]; if(sum > submax) submax = sum; } if(submax>max) max = submax; } return max; } }
2.采用动态规划法，时间复杂度为O（n）
public class Solution { public int FindGreatestSumOfSubArray(int[] array) { if(array.length == 0) return 0; int sum = array[0]; int tempsum = array[0]; for(int i = 1;i<array.length;i++){ tempsum = (tempsum<0)?array[i]:tempsum + array[i]; sum = (tempsum > sum) ? tempsum : sum; } return sum; } }
31.1—n整数中1出现的次数
时间复杂度为O(nlogn)
public class Solution { public int NumberOf1Between1AndN_Solution(int n) { int number = 0; for(int i=1;i<=n;i++){ number = number+numberOf1(i); } return number; } public int numberOf1(int i){ int number = 0; while( i!= 0){ if(i % 10 ==1) number++; i = i/10; } return number; } }
时间复杂度为O（logn）
//主要思路：设定整数点（如1、10、100等等）作为位置点i（对应n的各位、十位、百位等等），分别对每个数位上有多少包含1的点进行分析 //根据设定的整数位置，对n进行分割，分为两部分，高位n/i，低位n%i //当i表示百位，且百位对应的数>=2,如n=31456,i=100，则a=314,b=56，此时百位为1的次数有a/10+1=32（最高两位0~31），每一次都包含100个连续的点，即共有(a%10+1)*100个点的百位为1 //当i表示百位，且百位对应的数为1，如n=31156,i=100，则a=311,b=56，此时百位对应的就是1，则共有a%10(最高两位0-30)次是包含100个连续点，当最高两位为31（即a=311），本次只对应局部点00~56，共b+1次，所有点加起来共有（a%10*100）+(b+1)，这些点百位对应为1 //当i表示百位，且百位对应的数为0,如n=31056,i=100，则a=310,b=56，此时百位为1的次数有a/10=31（最高两位0~30） //综合以上三种情况，当百位对应0或>=2时，有(a+8)/10次包含所有100个点，还有当百位为1(a%10==1)，需要增加局部点b+1 //之所以补8，是因为当百位为0，则a/10==(a+8)/10，当百位>=2，补8会产生进位位，效果等同于(a/10+1)
public class Solution { public int NumberOf1Between1AndN_Solution(int n) { int count=0; int i=1; for(i=1;i<=n;i*=10) { //i表示当前分析的是哪一个数位 int a = n/i,b = n%i; if(a%10==1) count=count+(a+8)/10*i+a%10*(b+1); else count=count+(a+8)/10*i; } return count; } }
32.把数组排成最小的数
题目描述
输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。
例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。
* 解题思路： * 先将整型数组转换成String数组，然后将String数组排序，最后将排好序的字符串数组拼接出来。关键就是制定排序规则。 * 排序规则如下： * 若ab > ba 则 a > b， * 若ab < ba 则 a < b， * 若ab = ba 则 a = b； * 解释说明： * 比如 "3" < "31"但是 "331" > "313"，所以要将二者拼接起来进行比较
import java.util.ArrayList; import java.util.Collections; import java.util.Comparator; public class Solution { public String PrintMinNumber(int [] numbers) { /** * 1.用list装numbers数组中的数 * 2.使用collection.sort进行排序，排序是将str1+""+str2和str2+""+str1的大小进行比较 * 3.将排序后的数组进行拼接 */ if(numbers == null || numbers.length==0) return ""; ArrayList<Integer> list = new ArrayList<Integer>(); for(int i:numbers){ list.add(i); } Collections.sort(list, new Comparator<Integer>(){ public int compare(Integer str1,Integer str2){ String s1 = str1 + "" + str2; String s2 = str2 + "" + str1; return s1.compareTo(s2); } }); StringBuffer sb= new StringBuffer(); for(int i:list) sb.append(i); return sb.toString(); } }
33.丑数
题目描述
把只包含因子2、3和5的数称作丑数（Ugly Number）。
例如6、8都是丑数，但14不是，因为它包含因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
思路：
所有的丑数分为三种类型 2*i,3*i,5*i 其中 i是数组中的元素，一开始只有1
2*1 3*1 5*1
2*2 3*1 5*12*2 3*2 5*1
2*3 3*2 5*1
2*3 3*2 5*2
2*4 3*3 5*2
2*5 3*3 5*2
2*5 3*4 5*2
2*6 3*4 5*3
2*8 3*5 5*3
2*8 3*6 5*4
public class Solution { public int GetUglyNumber_Solution(int index) { if(index<7) return index; int[] ret = new int[index]; ret[0] =1; int t2 = 0;int t3= 0; int t5=0; for(int i=1;i<index;i++){ ret[i]=Math.min(Math.min(ret[t2]*2, ret[t3]*3), ret[t5]*5); if(ret[i] == ret[t2]*2) t2++; if(ret[i] == ret[t3]*3) t3++; if(ret[i] == ret[t5]*5) t5++; } return ret[index-1]; } }
34.第一次只出现一次的字符
题目描述
在一个字符串(1<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置
import java.util.*; public class Solution { public int FirstNotRepeatingChar(String str) { if(str == null || str.length() == 0) return -1; char[] strArray = str.toCharArray(); LinkedHashMap<Character,Integer> map = new LinkedHashMap<Character,Integer>(); for(char a:strArray){ if(map.containsKey(a)){ map.put(a, map.get(a)+1); }else map.put(a, 1); } for(char key:map.keySet()){ if(map.get(key)==1) return str.indexOf(key); } return -1; } }
35.数组中的逆序对
题目描述
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。
输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
归并排序的改进
public class Solution { public int InversePairs(int [] array) { if(array==null||array.length==0) { return 0; } int[] copy = new int[array.length]; for(int i=0;i<array.length;i++) { copy[i] = array[i]; } int count = InversePairsCore(array,copy,0,array.length-1);//数值过大求余 return count; } private int InversePairsCore(int[] array,int[] copy,int low,int high) { if(low==high) { return 0; } int mid = (low+high)>>1; int leftCount = InversePairsCore(array,copy,low,mid)%1000000007; int rightCount = InversePairsCore(array,copy,mid+1,high)%1000000007; int count = 0; int i=mid; int j=high; int locCopy = high; while(i>=low&&j>mid) { if(array[i]>array[j]) { count += j-mid; copy[locCopy--] = array[i--]; if(count>=1000000007)//数值过大求余 { count%=1000000007; } } else { copy[locCopy--] = array[j--]; } } for(;i>=low;i--) { copy[locCopy--]=array[i]; } for(;j>mid;j--) { copy[locCopy--]=array[j]; } for(int s=low;s<=high;s++) { array[s] = copy[s]; } return (leftCount+rightCount+count)%1000000007; } }
没看懂。。。
