希尔排序
希尔排序(Shell sort)这个排序方法又称为缩小增量排序(diminishing increment Sort),是1959年由D.L.Shell提出来的。该方法的基本思想是:设待排序元素序列有n个元素,首先取一个整数gap<n作为间隔,将全部元素分为gap个子序列,所有距离为gap的
例如取gap=[gap/21,重复上述的子序列划分和排序工作。直到最后取gap==1,将所有元素放在同一个序列中排序为止。由于开始时gap的取值较大,每个子序列中的元素较少,排序速度较快;待到排序的后期,gap取值逐渐变小,子序列中元素个数逐渐变多,但由于前
面工作的基础,大多数元素已基本有序,所以排序速度仍然很快。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,具体算法描述:
选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
按增量序列个数k,对序列进行k 趟排序;每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
举个栗子
原始序列:84、83、88、87、61、50、70、 60、80、99
1)第一趟,84对应50,50比84小,交换。
结果:[ 50]、83、88、87、61、[84]、70、 60、80、99
2) 第二趟,83对应70,70比83小,交换。
结果:50、[70]、88、87、61、84、[83]、 60、80、99
3)依次如此,把剩余的都按这样排好。
结果:50、70、60、80、61、84、83、 88、87、99
4)缩小间隔步幅为2,分别对其进行插入排序
结果:50、70、60、80、61、84、83、 88、87、99
…
5)依次类推知道步幅间隔为1
结果: 50、60、61、70、80、83、84、 87、88、99
最后如果还没有理解这个过程的话,小编放上一个动图,让大家更深入的理解这个过程:
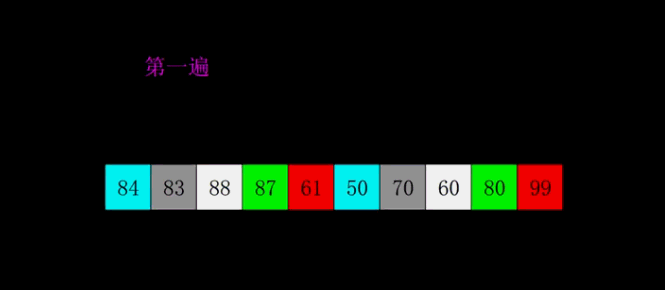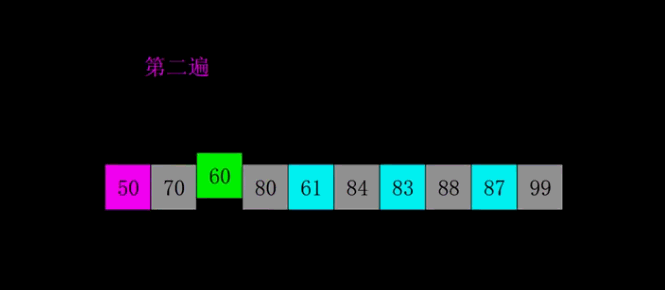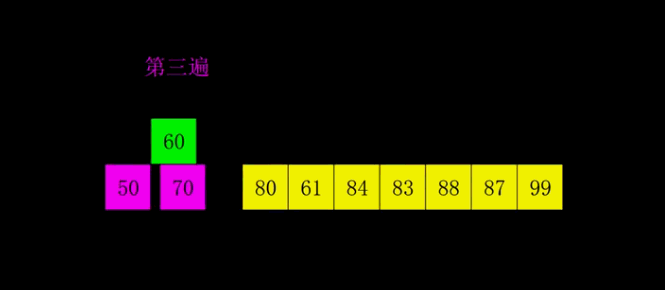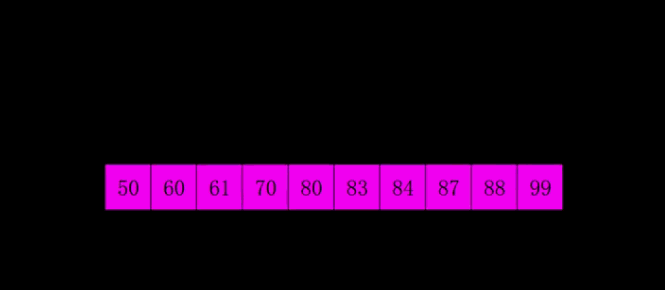
接下来就是希尔排序的算法实现喽
希尔排序C++实现代码:
#include <iostream>
using namespace std;
#include <vector>
#include <time.h>
vector<int> get_random(int n, int N);
const int MAX_NUM=10000;
int data[100];//定义一个产生数组储存100个随机数
void ShellSort(int n);//直接插入排序
void output(int n);
int main()
{
srand((unsigned int)time(0));
vector<int> randsample=get_random(100,MAX_NUM);//产生100个0-MAZX_NUM的随机数,每次产生的随机数不一样
int size=randsample.size();
//输出最开始时未排序时的顺序:
cout<<"随机数的顺序:"<<endl;
for(int i=0;i<randsample.size();i++)
{
cout<<randsample[i]<<" ";
}
cout<<endl;
clock_t start,finish;//定义一个测量一段程序运行时间的前后值
double totaltime;//总的运行时间
//测试希尔排序
cout<<"执行希尔排序后:"<<endl;
for(int i=0;i<randsample.size();i++)
{
data[i]=randsample[i];
}
start=clock();
ShellSort(size);
finish=clock();
output(size);
totaltime=(double)(finish-start)/CLOCKS_PER_SEC;
cout<<"运行时间:"<<totaltime<<endl;
}
//产生随机数的函数
vector<int> get_random(int n, int N)
{
vector<int> vec(N);//N代表初始状态分配的空间大小
vector<int> out_vec;
for(int i=0;i<N;++i)
{
vec[i]=i;
}
for (int i=0;i<n;++i)
{
int rand_value=rand()%N;
out_vec.push_back(vec[rand_value]);
vec[rand_value]=vec[N-1];//将数组vec的元素
N--;
}
return out_vec;
}
void ShellSort(int n)
{
int i,j;
int gap=n+1;
int temp;
int count=0;
int count1=0;
while(gap>1)
{
gap=gap/3+1;//求下一增量值
for(i=gap;i<n;i++){//各个子序列交替处理
if(data[i]<data[i-gap]){//逆序
count++;
temp=data[i];
j=i-gap;
while (j>=0&&temp<data[j]) {
count++;
data[j+gap]=data[j];//后移元素
count1++;
j=j-gap;//再比较前一元素
}
data[j+gap]=temp;
}
}
}
cout<<"比较次数: "<<count<<" 移动次数: "<<count1<<endl;
}
void output(int n)
{
for(int i=0;i<n;i++)
{
cout<<data[i]<<" ";
}
cout<<endl;
}

希尔排序Java代码实现
import java.util.ArrayList;
import java.util.List;
import java.util.Random;
public class ShellSort
{
public static void main(String[] args)
{
Object []arr = getRandomNumList(100,0,10000).toArray();
int[] ins = new int [100] ;
System.out.println("排序前:");
for(int i = 0; i < arr.length; i++) {
String s=arr[i].toString();
ins[i]= Integer.parseInt( s );
System.out.println(ins[i]);
}
System.out.println("排序后:");
int[] ins2 = shellSort(ins);
for(int i = 0; i < arr.length; i++) {
System.out.println(ins2[i]);
}
}
public static int[] shellSort(int[] data){
int i,j;
int n = data.length;
int gap=n+1;
int temp;
while(gap>1)
{
gap=gap/3+1;//求下一增量值
for(i=gap;i<n;i++){//各个子序列交替处理
if(data[i]<data[i-gap]){//逆序
temp=data[i];
j=i-gap;
while (j>=0&&temp<data[j]) {
data[j+gap]=data[j];//后移元素
j=j-gap;//再比较前一元素
}
data[j+gap]=temp;
}
}
}
return data;
}
//定义生成随机数并且装入集合容器的方法
//方法的形参列表分别为:生成随机数的个数、生成随机数的值的范围最小值为start(包含start)、值得范围最大值为end(不包含end) 可取值范围可表示为[start,end)
public static List getRandomNumList(int nums,int start,int end){
//1.创建集合容器对象
List list = new ArrayList();
//2.创建Random对象
Random r = new Random();
//循环将得到的随机数进行判断,如果随机数不存在于集合中,则将随机数放入集合中,如果存在,则将随机数丢弃不做操作,进行下一次循环,直到集合长度等于nums
while(list.size() != nums){
int num = r.nextInt(end-start) + start;
if(!list.contains(num)){
list.add(num);
}
}
return list;
}
}
希尔排序Python代码实现
import random
def shellsort(lists):
#希尔排序
count = len(lists)
step = 2
group = round(count / step)
while group > 0: #通过group增量分组循环
for i in range(0, group):
j = i + group
while j < count: #分组中key值的索引,通过增量自增
k = j - group
key = lists[j]
while k >= 0: #分组中进行插入排序
if lists[k] > key:
lists[k + group], lists[k] = lists[k], key
else: break
k -= group
j += group
group = round(group/step)
return lists
def main():
arr =[]
while(len(arr)<100):
x=random.randint(0,10000)
if x not in arr:
arr.append(x)
shellsort(arr)
print(arr)
if __name__ == "__main__":
main()
算法分析:
增量gap的取法有各种方案。最初Shell提出gap=n/2,gap=gap/2,直到gap=1.但由直到最后一步,在奇数位置的元素才会与偶数位置的元素进行比较,这样使这个序列的效率将很低。后来Knuth提出取gap=gap/3+1。还有人提出都取为好,也有人提出各gap互质为好。应用不同的序列会使希尔排序算法的性能有很大差异,有些序列的效率会明显更高,例如:1,8,23,77,281,1073,4193,16577。
对希尔排序的时间复杂度的分析很困难,在特定情况下可以准确地估算排序码的次数和元素移动次数,但想要弄清排序码比较次数和元素移动次数与增量选择之间的依赖关系,并给出完整的数学分析,还没有人能够做到。
由于即使对于规模较大的序列(n<=1000),希尔排序都具有很高的效率。并且希尔排序算法的代码简单,容易执行,所以很多排序应用程序都选用了希尔排序算法。希尔排序是一种不稳定的排序算法。
继续加油!
以上就是本次给大家分享的希尔排序的几种实现,如果有什么不足之处欢迎大家指出,留言。如果有什么写的不好的地方欢迎大家补充,希望得到大家的支持,下面我会持续更新其他的排序算法,敬请期待!
(博客在今天开通了评论功能,欢迎大家一起来讨论交流啊)
大家如果对博客的搭建,一些算法的分享可以来我的个人博客溜达溜达



 浙公网安备 33010602011771号
浙公网安备 33010602011771号