前面的《自动扫雷》系列博文介绍了如何从XP自带的扫雷游戏中获取游戏、分析确定情况下的雷块,以及操作鼠标完成游戏。这篇将介绍如何使用数学中的概率知识来玩扫雷游戏,也正是本人最想介绍的地方,即《前言》中所说的第四种扫雷模型的分析。
先看游戏界面,如下:

在游戏开始时,如何出现这样的情况,我们可以认为游戏中未显示块按概率相等可分为四个区域,其中a,b,c是其中的三个区域(a区域指上面的5个块,b区域指中间的3个块,c区域指下面的5个块),再加上不与已揭开块相邻的所有块构成一个区域d(d区域含有465块)。那么这四个区域中哪个区域有雷的概率最小呢?
这里直接说明所使用的数学方法叫做——条件概率和全概率公式。
条件概率可以说是计算机领域的一个功臣,由其发展而来的“统计语言模型”实现了机器翻译、语音识别、汉字识别等一系列的用传统方法很难解决的问题。而以其为基础的“贝叶斯公式”在图像处理、决策支持系统和博弈论中有着广泛的应用。
维基百科中给的定义是:条件概率就是事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为P(A|B),读作“在B条件下A的概率”。
而全概率为:
假设{ Bn : n = 1, 2, 3, ... } 是一个概率空间的有限或者可数无限的分割,且每个集合Bn是一个可测集合,则对任意事件A有全概率公式:
又因为
此处Pr(A | B)是B发生后A的条件概率,所以全概率公式又可写作:
用自己的话说,条件概率是在某件事发生的情况下,另一件事的概率;全概率是将所有情况的概率加起来。
而在扫雷游戏中有什么“所有情况”呢?
看上面的游戏场景,a,b,c所占的13个块,如果仅仅根据上面所显示的"1","2",可以说这13个块中,雷的总数可以有2个,也可以有3个!!并且有2个或者3个的概率分别是1/2。
那么其情况如下:

上表说明当雷数为2时,abc有雷的概率分别为0,1/3,1/5;当雷数为3时,abc有雷的概率分别为1/5,0,2/5。
可算出
a区域有雷的概率为0*1/2+(1/5)*(1/2)=1/10
b区域有雷的概率为(1/2)*(1/3)+0*1/2=1/6
c区域有雷的概率为(1/2)*(1/5)+(1/2)*(2/5)=3/10
而d区域的概率同理也算出为(1/2)*(97/465)+(1/2)*(96/465)=193/930
可知,a区域有雷的概率最小,故可以在此5块中随机选一块点击了,然后一切就交给上苍了~~(在不用类似查看内存的方法的情况下,人做的就只有这么多了)
到此,数学原理已介绍完毕,用一句话总结,即,先找出按区域划分的未显示块,然后分类讨论这些区域中雷的总个数。接下来的一篇博文(也是本系列最后一篇),将介绍如何将上面的数学运算用程序代码实现。
批注:从自己想到数学实现到想明白如何用程序代码实现,应该有两年之多,当然只是偶尔无聊时才思考一下。不过,在思考这个实现过程中,自己开始一直在用数学的思路而没有用代码的思路去思考,故一直行不通。当自己用代码实现后,感觉自己的思维又有了新的提高~~

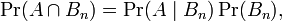



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 从 HTTP 原因短语缺失研究 HTTP/2 和 HTTP/3 的设计差异
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 分享 3 个 .NET 开源的文件压缩处理库,助力快速实现文件压缩解压功能!
· Ollama——大语言模型本地部署的极速利器
· DeepSeek如何颠覆传统软件测试?测试工程师会被淘汰吗?