模型量化-嵌入式深度学习4

嵌入式深度学习-硬件与算法协同优化

本系列博客主要以Bert Moons《Embedded Deep Learning》翻译而成

Goetschalckx K, Moons B, Lauwereins S, Andraud M, Verhelst M (2018) Optimized hierarchical cascaded processing. IEEE J Emerging Sel Top Circuits Syst. https://doi.org/10.1109/JETCAS.2018.2839347

本文概述了模型量化的方法与能耗比较。

测试时定点神经网络（Test-Time Fixed-Point Neural Networks）

测试时定点神经网络（Test-Time Fixed-Point Neural Networks，FPNN）是以低精度运行的网络。它们使用浮点数进行预训练，并根据训练后定点分析的结果在推理之前进行量化。这项工作的意义在于：

• 表明可以通过对某一层的输入和权重在测试时量化，从而在多种CNN中调节计算精度。每个CNN所需要的最低计算精度会因网络结构、应用甚至每个层而存在差异。
• 表明CNN通常是非常稀疏的，可以通过跳过冗余的稀疏计算来降低能量消耗。

量化

对于[-1,1]区间上的权重或输入\(x\)，通过以下函数进行量化： $$q=clip(\frac{round(2^{Q-1} \times x)}{2^{Q-1}}, -1,1-2^{-(Q-1)})$$

在对权重和输入进行量化之前，根据它们的值将它们适当地重新缩放到[-1,1]区间上。该缩放方式与将结果乘以2或将数据以定点数表示形式进行移位在数学上是相同的，因此该操作在硬件上执行的代价非常小。

一致性重缩放与分层重缩放

• 一致性重缩放：将单个量化方案用于网络中的所有层。所有输入和权重均以相同的值进行缩放。
• 分层重缩放：输入和权重在每层的基础上进行缩放。例如第1层权重都在[-0.5, 0.5]之间，第6层权重在[-0.0625, 0.0625]区间内，也成为“动态定点”
• 分层重缩放更加精细和有效。

分层量化

网络也可以具有分层量化而不是用相同位数量化网络的所有权重和输入。通过利用特定层的输入和权重分布的变化找到每个层的最佳位宽设置。

• 可以更精确地设置工作点（即所需的最小相对准确率）。这可以控制能耗-准确率的折中。
• 更好地权衡能耗与准确性。

为了找到每层的最优量化设置，需对参数进行贪婪搜索：从第一层开始，对其输入进行量化，直到准确率降至目标准确率为止。接下来输入的量化保持固定，通过相同的方式最大化权重的量化设置。在下一层中应用相同的过程，直到最后一层。
有一个普遍趋势：网络的较低层所需的位宽比较高层要少。这部分是由于向前参数扫描，但可以假设较低层与较高层之间的输入和权重的统计差异也有影响。

稀疏FPNN的能耗

量化和ReLU都会导致0的产生，增加了网络稀疏性，从而实现了能耗的降低

零值的跳过需要硬件支持，所以这是一种硬件-算法协同优化方法。在专用硬件加速器中存在标志位指示即将到来的数据是否为0，并阻止电路翻转。

训练时量化神经网络（QNN）

注：普通CPU和GPU仅原生支持有限的计算精度设置，如32-64浮点或8-16位整数运算，无法受益于低精度QNN。而在定制设计的ASIC中，可以根据给定条件选择最佳计算精度，以最小化每次网络推理的能量消耗。QNN优于FPNN。

输入层

• 第一层输入为int8
• 其他层的所有输入都被量化为intQ

如果M是输入位数，M>Q，那么intQ层可以表示为一系列移位和加法的点积操作。
可以使用以下编码方式在intQ硬件上处理M>Q的输入：

\[s=x \cdot w_Q \Longleftrightarrow s= \sum_{n=1}^{M / Q}(2^Q)^{n-1}(x^n \cdot w_Q) \]

在这里，\(x^{M/Q}\)是基数\(Q\)中输入向量\(x\)的最高有效位（Most Significant Bit），\(x^1\)是最低有效位（Least Significant Bit）。\(w_Q\)量化为intQ的权重向量，s是所得的加权和。

训练时量化权重（Train-Time Quantized Weights）

所有权重都以定点表示量化为Qbit。使用以下确定性量化函数进行前向传播：$$q=clip(\frac{round(2^{Q-1} \times w)}{2^{Q-1}}, -1,1-2^{-(Q-1)})$$
Q=1的情况被视为特例，其中q = Sign(w)。使用“直通估算器”（straight-through estimator，STE）函数在离散的神经元中进行梯度的反向传播。如果梯度\(\frac{∂C}{∂q}\)已被一个估算器\(g_q\)获得，则\(\frac{∂q}{∂w}\)的STE为：$$STE = hardtanh(w) = clip(w,−1, 1)$$

STE的\(\frac{∂C}{∂w}\)为：$$g_w=g_q \times clip(w,-1,1)$$

根据（Hubara et al. 2016a）的做法，在训练过程中所有实值权重都被限制在区间[-1, 1]内。否则，实值权重会变得很大，而不会对量化后的权重产生影响。不同Q下的权重量化函数q(w)和STE函数绘制在图3.15中。

\(g_w = g_q * hardtanh(w)\)可以简化为：
当 -1 ≤ w ≤ 1 时，STE = \(g_q\)
当 w < -1 或 w > 1 时，STE = 0

训练时量化激活值（Train-Time Quantized Activations）

在量化神经网络（QNN）中，所有激活值以定点表示量化到 Q 个比特数。前向传播中使用以下确定性量化激活函数：

\[A_{ReLU}=max(0,q(a)) \]

\[A_{hardtanh}=qhardtanh(a) \]

\[qhardtanh(a) = 2 × hardtanh(round(hardsigmoid(a) × 2^{Q−1})/2^{Q−1}), \]

\[hardsigmoid(a) = clip((a + 1)/2, 0, 1) \]

二值网络中有\(A_{hardtanh}=Sign(a)\)

反向传播中使用以下STE函数进行梯度估计：

\[g_{ReLU} = max(0, hardtanh(a)) \]

\[g_{hardtanh} = hardtanh(a) \]

训练时所有实值激活值都被限制在区间[-1, 1]内。

量化训练

需要从头开始训练QNN，因为浮点预训练网络通常不是QNN的一个合适的初始化点。

QNN的能耗

3.2的模型中，n=1.25

聚类神经网络

• 对权重和激活进行聚类，将浮点网络进行压缩。一组权重或激活值被K-means聚类成n个簇以确保只剩少数不同的权重。然后，每个出现的权重或激活值通过\(\log_2(n)\)位的小索引指向一个小查找表中的真值。
• 在初始的聚类步骤之后，对聚类的值进行重新训练以提高网络的准确率。
• 实际值以高精度浮点数或定点数的形式存储，计算使用16位，但压缩了数据传输和存储的成本。

拓展阅读

• 量化神经网络
  • 量化方法：https://www.jiqizhixin.com/graph/technologies/62727532-3d31-45d4-975f-5d68ce194d24
  • 量化方法：https://zhuanlan.zhihu.com/p/419052103
• FP16和FP8：

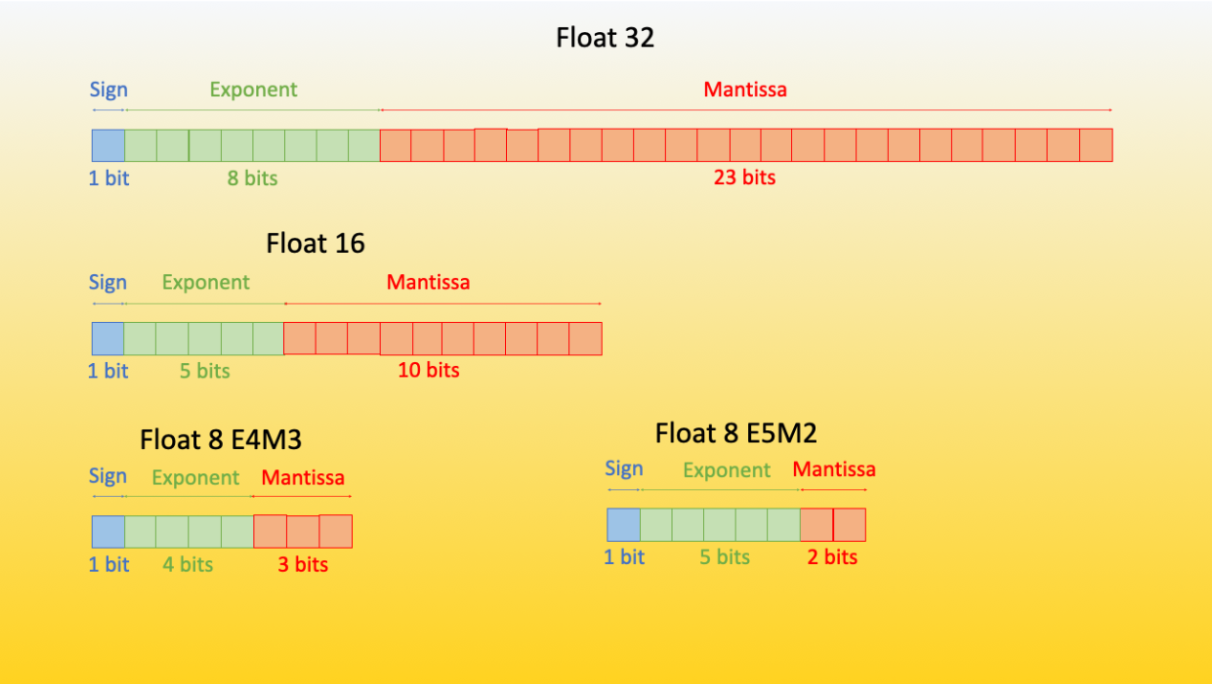
FP8两种不同的编码方式: E4M3 (4 位指数，3 位尾数) 和 E5M2 (5 位指数，2 位尾数)。E4M3 格式可以表示的浮点数范围为 -448 到 448。而 E5M2 格式因为增加了指数位数，其表示范围扩大为 -57344 到 57344 - 但其相对 E4M3 而言精度会有损失，因为两者可表示的数的个数保持不变。经验证明，E4M3 最适合前向计算，E5M2 最适合后向计算。

• FP4 精度简述
  符号位表示符号 (+/-)，指数位转译成该部分所表示的整数的 2 次方 (例如 2^{010} = 2^{2} = 4 )。分数或尾数位表示成 -2 的幂的总和，如果第 i 位为 1 ，则和加上 2^-i ，否则保持不变，这里 i 是该位在比特序列中的位置。例如，对于尾数 1010，我们有 (2^-1 + 0 + 2^-3 + 0) = (0.5 + 0.125) = 0.625 ，然后，我们给分数加上一个 1 ，得到 1.625 。最后，再将所有结果相乘。举个例子，使用 2 个指数位和 1 个尾数位，编码 1101 对应的数值为:

  -1 * 2^(2)*(1 + 2^-1) = -1 * 4 * 1.5 = -6
  

  FP4 没有固定的格式，因此可以尝试不同尾数/指数的组合。一般来说，在大多数情况下，3 个指数位的效果会更好一些。但某些情况下，2 个指数位加上 1 个尾数位性能会更好。

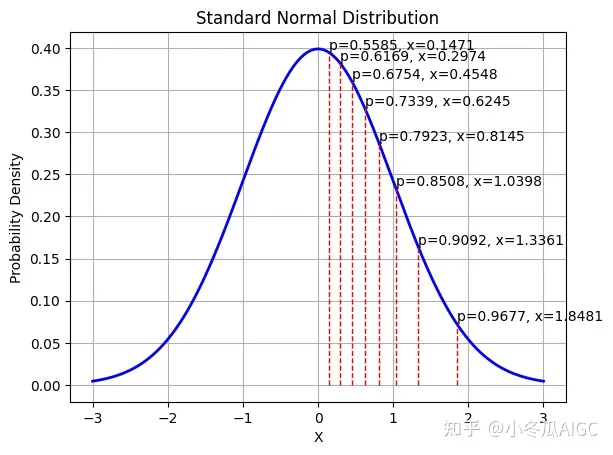
• NF4 精度简述

  NF4是建立在分位数量化技术的基础之上的一种信息理论上最优的数据类型。把4位的数字归一化到均值为 0，标准差为 [-1,1] 的正态分布的固定期望值上。