硬件算法协同优化-嵌入式深度学习3
嵌入式深度学习-硬件与算法协同优化
本系列博客主要以Bert Moons《Embedded Deep Learning》翻译而成
Goetschalckx K, Moons B, Lauwereins S, Andraud M, Verhelst M (2018) Optimized hierarchical cascaded processing. IEEE J Emerging Sel Top Circuits Syst. https://doi.org/10.1109/JETCAS.2018.2839347
简介
硬件-算法协同优化主要利用神经网络的三个特性:
- 数据流优化:并行计算、数据重用
- 网络的稀疏性:很多模型权值为0或很小,或者数据经过某些节点以后会直接变为无用值
- 容错性:深度学习具有鲁棒性,对数据的误差不敏感

利用网络结构
抛弃通用处理器,开发专门针对目标算法的定制化硬件加速器来提高算法评估的能效,充分利用算法中已知的数据流来实现算法的并行执行和最小化数据搬运,如TPU
在一个网络层中的许多计算共享公共输入。每个权重参数在输出张量的同一切片的多次卷积中被重复使用大约 \(M_2\) 次,而每个输入数据点在输出张量的 \(F\) 个不同切片中被重复使用。此外,中间累加结果 \(o\) 必须累积 \(C \times k^2\) 次。在定制的加速器中可以以多种方式利用这一点进一步提高效率,超越高度并行但未经数据流优化的GPU。
-
数据复用可以通过 在多个并发的执行单元上复用同一数据,或在同一执行单元的不同时隙中复用数据利用 实现。可以区分为3种极端情况。但实际上大多数实现方式都是混合形。
- 在“权重并行”或“输入固定”的方法中(图3.3),同一输入数据与同一层的不同输出通道的若干权重相乘。在理想情况下,每个输入只需加载一次到系统中。然而,这对权重存储带宽(weight memory bandwidth)不利,因为每次产生新的输入时,都需要频繁地重新加载权重。此外,输出结果的累加(accumulation)不能在不同的时钟周期中完成,需要将中间结果缓存到存储器中以便之后重新取回,这严重影响了输入/输出存储器带宽(input/output memory bandwidth)。
- “权重固定”或“输入并行”的方法改善了权重存储带宽,但以输入存储带宽为代价。这里每个权重只需获取一次,并与许多输入值相乘。
- “输出固定”的方法在每个时钟周期重新加载新的权重和输入,并且能够在不同的时钟周期内累加中间结果,从而有利于输出的存储带宽。
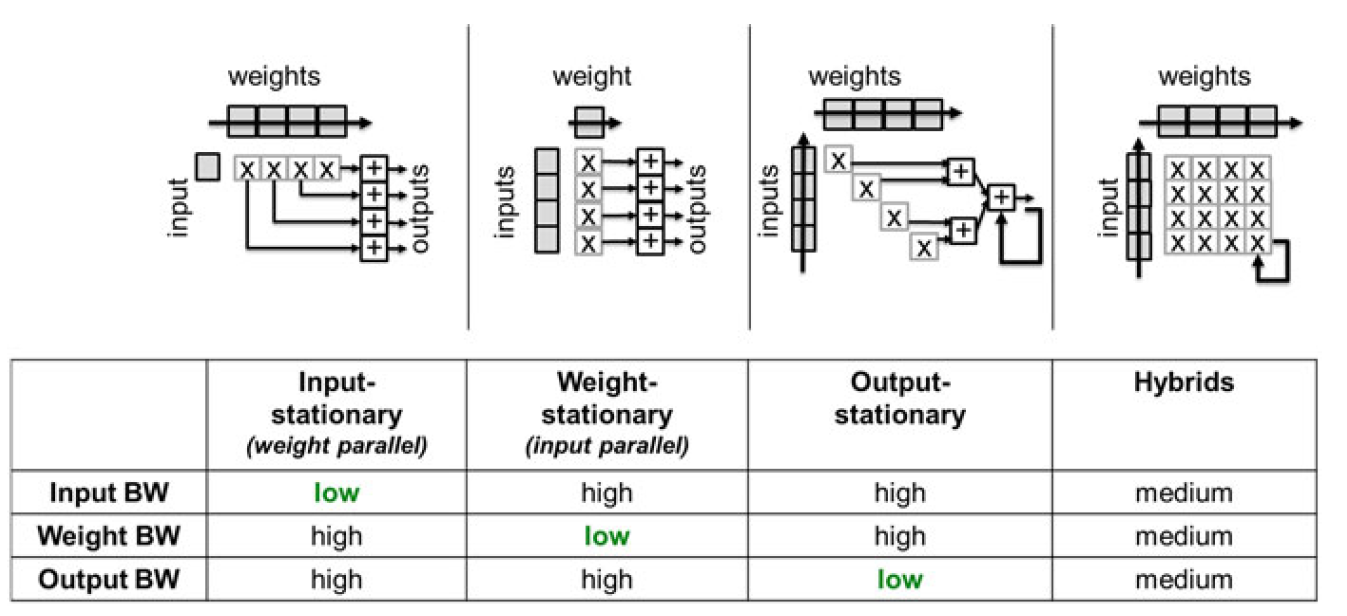
图中BW为带宽的意思 -
减少连续数据提取的能耗负担的一种补充方法是利用时间数据局部性来降低每次数据提取的能耗。大多数实际的深度网络需要非常多的权重和输入/输出内存(Mbytes to Gbytes),无法将它们全部放入芯片内存中,因此需要从能耗高昂的外部DRAM进行提取。与传统处理器类似,这可以通过一个或多个层次的芯片内SRAM或寄存器文件的内存层次结构来缓解。经常访问的数据可以被存储在本地,以降低其提取成本。与通用解决方案相比,一个重要的区别是内存层次结构中的内存大小可以根据网络的结构进行优化
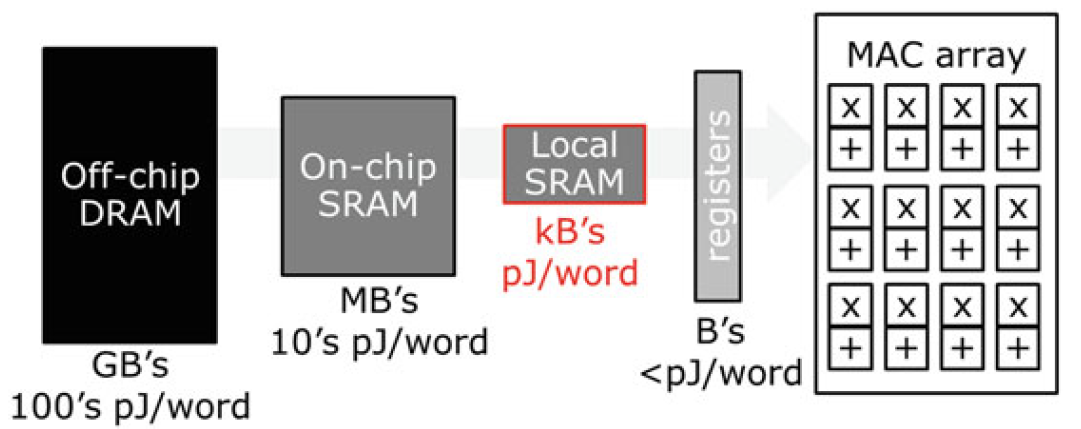
- 利用局部性的另一种方法是存内计算,即将计算集成在存储阵列内部,如在电阻式存储技术或闪存存储器中。
利用稀疏性
神经网络具有稀疏性。AlexNet超过70%的激活值为零。在降低位宽计算时,也有一些权重值被量化为零。使用ReLU、L1或L2正则化也可以使权重减为0或较小值
- 硬件方面,可以通过以下方式利用:
- 避免与0进行任何乘加运算
- 不从内存中获取0值数据
- 使用Huffman或其他类型的编码压缩片上或片外的数据流
- 算法层面,可以进行模型剪枝等操作。
利用容错性
- 使用低精度进行推理
- 在高能效的近阈值区域操作电路
低精度神经网络中的能量增益
通过调节精度利用神经网络的容错性,可以降低数字电路的有功功耗。这里提供一个基本的能耗模型。
一个数字系统的总功耗由动态功耗和漏电功耗两部分组成:
其中,\(\alpha\) 是电路的翻转率, \(f\) 是时钟频率,\(C\) 是总开关电容, \(V\) 是电源电压。通过调节精度(即动态缩放编码网络权重和输人的比特数),可以大大减少翻转率\(\alpha\) 。图3.6b说明了在典型数字乘法器中可实现的能量-准确率的折中。请注意,在1%均方根误差(RMSE)下,可以实现12倍能量增益。由于神经网络具有容错性,在这样的 RMSE下中间计算的性能可能不会降低。
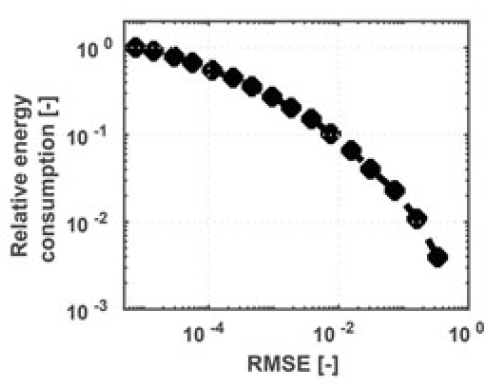
换句话说,通过降低神经网络的精度,可以减少开关活动度和总开关电容,从而降低动态功耗。此外,较低的精度还可以减少每一步计算所需的时钟周期数,进一步降低了总功耗。这些减少共同导致了显著的能量增益。
然而,降低精度也会引入一定的准确性损失。因此,为了平衡能量效率和模型精度之间的权衡,需要仔细选择最佳的精度级别。在实际应用中,根据具体的应用需求和系统要求来确定最佳的精度级别是非常重要的。
每次推理的全局能耗是与片外 DRAM 访存所消耗的能量和处理平台本身的能耗之和。因此,每个网络推理的总能耗为:
片外存储器访问能耗
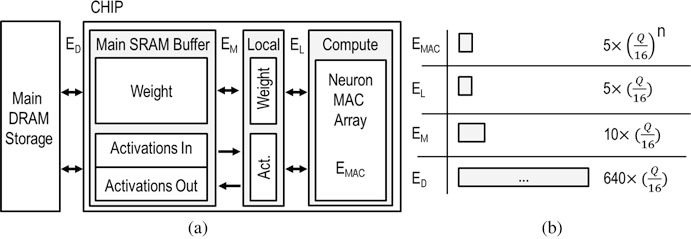
由于成本和漏电能耗的限制,常开芯片中的可用存储经常是有限的,因此通常不足以存储完整的模型和特征图。这种情况下,芯片将不得不频繁地与片外的存储系统进行通信。这样的接口成本要比一个等效的 MAC 操作高出两个数量级。如果实现的网络压缩可以使得网络完全存储在片上存储中,那么使用较少的比特位宽对权重和激活进行量化就有可能具有更高的能效。访问片外 DRAM 的能耗可以建模如下:
其中,\(E_D\)是每intQ DRAM访问所消耗的能量,如图3.7所示;\(s_{in}\),\(c_{in}\) 和\(M/Q\)分别是输入图像的尺寸,输入通道的数量以及第一层因数(见3.4.1节);\(f_{re-fetch}\)和\(w_{re-fetch}\)是间特征图或模型无法完全存储在片上的情况下必须从 DRAM 重新读取 /存储的字数。这些因素取决于所使用的切分方案和可用的片上存储容量。
硬件平台的一般性建模
如图 3-7 所示的硬件平台是一个典型的面向 CNN 的处理平台。它包含:
- 一个并发的神经元阵列,
- 一个有\(p\)个MAC 单元和两级片上 SRAM 存储的固定区域。
- 一个大型主缓冲区可以存储 \(M_W\) bit 的权重和 \(M_A = M_W\) bit的激活值,其中50%用于当前层的输入,50%用于当前层的输出。
- 一个较小的本地SRAM缓冲区主要存储当前正在使用的权重和激活值。
下面是计算能耗的过程,所有能耗都包含了控制、数据传输和时钟开销:
- 读写小的本地SRAM的能量消耗 \(E_L\) 被建模为单个MAC操作 \(E_{MAC}\) 的能耗
- 访问主要SRAM的成本为 \(E_M = 2 \times E_{MAC}\)
- 其他操作,如偏置(bias)相加、量化ReLU和非线性批归一化,也被建模为 \(E_{MAC}\)
那么,每次推理的芯片上总能耗是计算能耗 \(E_C\) 和访问权重的能耗 \(E_W\)以及访问激活值的能耗 \(E_A\) 的总和。在28纳米技术下测得16bit操作的能量\(E_{MAC} = 3.7 \text{pJ}\)。对SRAM缓冲区进行读/写操作的能量消耗被建模为 \(E_{SL} = 2E_{MAC}\) 和 \(E_{SM} = 10E_{MAC}\)。全局能量消耗为:
式中,\(E_C\) 是所有计算的能耗总和,包括部分积的产生、偏置相加、批归一化和激活
函数,通过评估 \(N_c\) 可以计算出这个值,\(N_c\) 是网络复杂度所对应的 MAC操作数;偏置相
加、批归一化和激活函数在每个输出特征点上以高精度(16bit) 运行,因此系数为 \(3 × A_s\)。\(N_s\)是模型的大小,\(A_s\)是整个网络中的中间输出特征总数。
权重从主缓冲区传输一次到本地缓冲区并在本地被复用,可以得到\(E_W\)的等式。这里 \(\sqrt{p}\) 是由于激活值的并行所导致的存储能耗的减少,因为一个权重会同时被 \(\sqrt{p}\) 个激活值使用。从主缓冲区中读取 /存储激活值可以推导得到同样的等式 \(E_A\) 。本地激活值的访问次数除以 \(\sqrt{p}\) ,这是因为一个激活值会同时乘以 \(\sqrt{p}\) 个权重。总并行度 \(p\) 是这些等式中的一个变量。取决于Q的值。一个2M的存储器可以存储超过2M个1位权重,但只能存储131k个16位权重。如果权重或特征图大小超过了片上可用存储的大小,则必须与较
大的片外 DRAM 存储器进行通信,如前(第3.2.1节)所述。


