DS博客作业02-栈和队列
0.PTA得分截图

1.1本周学习总结
栈
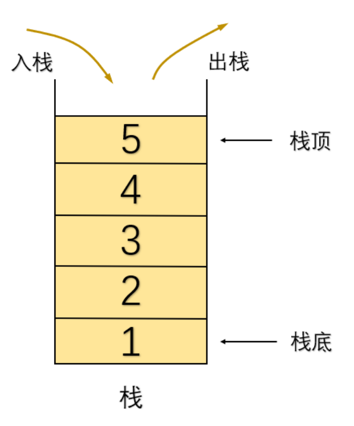
栈是一种是一种线性表,我们只能在栈的一端进行插入和删除操作,是先进后出的一种结构。允许插入删除的一端我们称为栈顶,而另一端不允许插入删除的我们称为栈底。
1.栈的存储结构
因为栈是一种线性表,所以栈可以采用和线性表相同的存储结构:顺序存储和链式存储。顺序存储结构的栈称为顺序栈,链式存储的栈称为链栈。
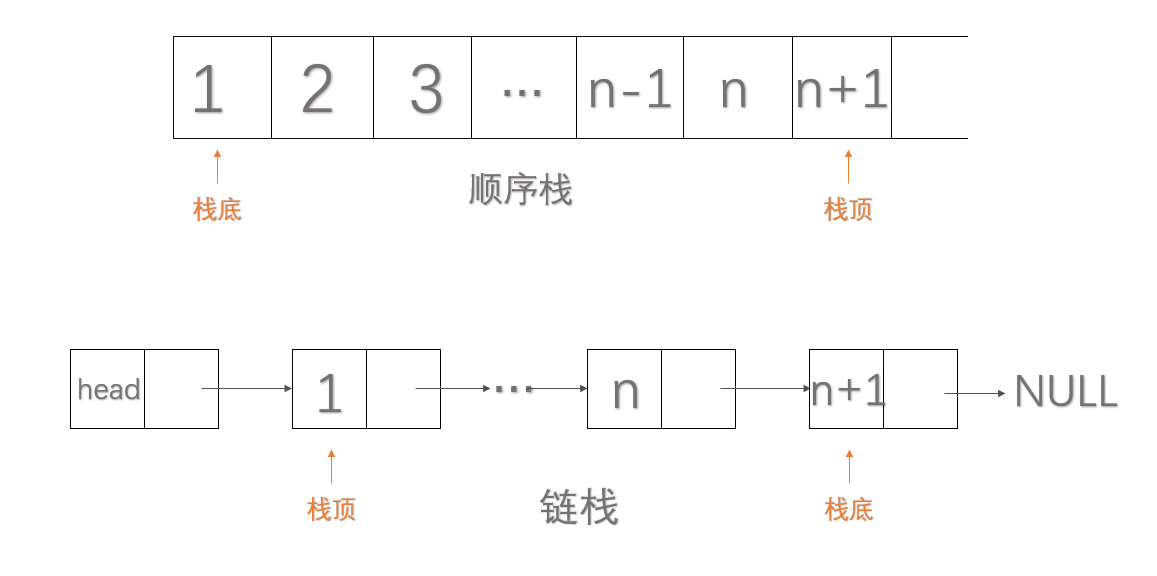
结构体定义
- 顺序栈
typedef struct
{
Elemtype data[MaxSize];
int top;//栈顶指针;
}SNode;
- 链栈
typedef struct stack
{
Elemtype data;
struct stack* next;
}SNode,*Stack;
2.栈的基本操作
- 初始化栈
将栈初始化为一个空栈,方便我们后续对栈进行操作。
/*顺序栈*/
void InitStack(SNode &s)
{
s.top=-1;//一般的顺序表栈顶指针的初始化为-1,
}
/*链栈*/
void InitStack(Stack &s)
{
s = new SNode;//申请空间;
s->next=NULL;
}
- 判断是否为空栈
我们都知道当我们如果要访问某个地址时,一定要先判断该地址中是否已经保存了数据,否则访问就会出现错误。所以我们要先判断该栈是否是一个空栈,以保证后续访问操作的进行。
/*顺序栈*/
bool IsEmpty(SNode s)//如果为空返回true,不为空则返回false;
{
if(s.top==-1)
return true;
else
return false;
}
/*链栈*/
bool IsEmpty(Stack s)//如果为空返回true,不为空则返回false;
{
if(s->next==NULL)
return true;
else
return false;
}
- 判断是否栈满
对于顺序栈来说,是用数组来保存数据,因为数组在被定义时就需要预先申请一段连续的空间,所以如果我们要往里面进行插入的操作,必须要先判断该栈是否已经满了,否则就会出现数组溢出,访问错误的情况。
/*顺序栈*/
bool IsFull(sNode s)
{
if(s.top==MaxSize-1)
return true;
else
return false;
}
/*链栈*/
因为是链式存储结构,不用预先设定需要多少的存储空间来保存数据,都是现用现配,空间利用效率比较高。所以只要一个数据我们就可以直接进栈,不必考虑是否会栈满。
- 进栈
对栈的一端进行插入。
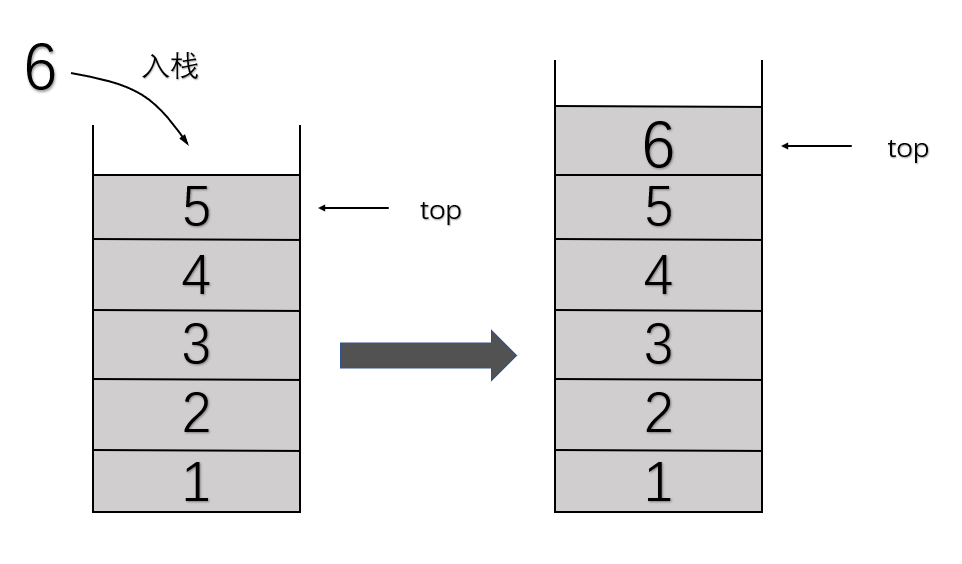
/*顺序栈*/
bool Push(SNode &s,Elemtype e)
{
if(IsFull(s))//在进栈之前一定要先判断是否栈满!
return false;//返回错误;
else
s.data[++s.top] = e;
return true;//说明进栈成功;
}
/*链栈*/
void Push(Stack &s,Elemtype e)//使用头插法;
{
Stack str;
str=new Stack;
str->data = e;
str->next= s->next;//先将原来的链栈连接到str后面;
s->next = str;//再将str连接到头结点后面成为新的栈顶;
}
- 取栈顶
取得栈顶元素。
/*顺序栈*/
bool Gettop(SNode &s, Elemtype &e)
{
if(IsEmpty(s))//取栈顶时要判断是否为空栈!
return false;
else
e = s.data[s.top];
return true ;
}
/*链栈*/
bool Gettop(Stack &s,Elemtype &e)
{
if(IsEmpty(s))//取栈顶时要判断是否为空栈!
return false;
else
e = s->next->data;
return true;
}
- 出栈
将栈顶元素删除,并移动栈顶指针。

/*顺序栈*/
bool Pop(SNode &s,Elemtype &e)//出栈并返回该栈顶元素;
{
if(IsEmpty(s))//在出栈之前一定要判断是否为空栈!
return false ;//出栈错误;
else
e = s.data[s.top--];//这里只是移动了栈顶指针,并没有真正的删除数据;
return true;//出栈成功;
}
/*链栈*/
void Pop(Stack & s,Elemtype &e)
{
Stack str;
if(IsEmpty(s))//出栈之前要判断是否为空栈;
return false;
else
{
e = s->next->data;
str = s->next;
s->next = str->next;//让头结点连接栈顶的下一个结点,使s->next->next成为新的栈顶;
delete str;//释放空间,这里数据是真的被删除
}
}
- 销毁栈
销毁栈释放其空间。
/*顺序栈*/
void DestroyStack(SNode &s)
{
delete s;
}
/*链栈*/
void DestroyStack(Stack &s)
{
ListStack str;
while(s!=NULL)
{
str = s;//str保存当前删除的结点
s = s->next;//s指向下一个需要删除的结点;
delete str;
}
}
3.共享栈
如果想要用到两个相同类型的栈,可以用一个数组data[]来实现这两个栈,这个栈称为共享栈。数组两端分别为两个栈的栈底。
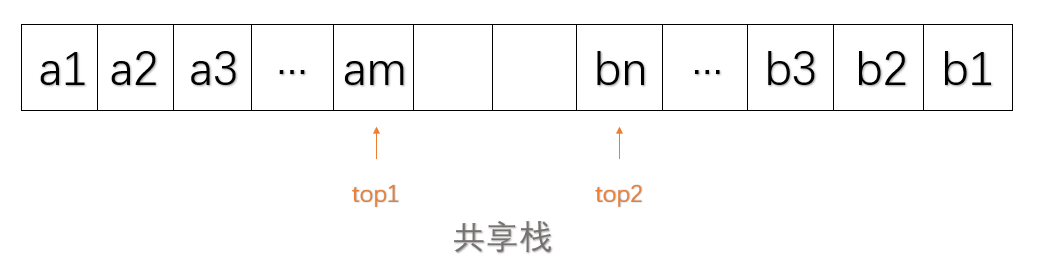
结构体定义
这里的结构体定义与上面的顺序栈结构体定义略有不同,上面是直接定义一个数组data[]来保存数据,而这里则是定义了一个指针data用来指向保存数据的数组,所以这里我们需要自己再申请相对应大小的空间来保存数据;
typedef struct
{
Elemtype *data ;//存储元素的数组;
int top1,top2;//两个栈顶指针;
int MaxSize;//栈堆最大的容量
}SNode,*Stack;
基本操作
pta 6-2 在一个数组中实现两个堆栈
- 实现创建两个栈堆
- 思路:
Stack CreateStack(int MaxSize)
{
定义一个结构体指针s;//因为函数返回的是Stack类型,所以我们返回的s必须是Stack类型;
为s申请空间;
为数组指针s->Data申请一段大小为MaxSize的空间
初始化两个栈顶指针;
}
-
代码实现:
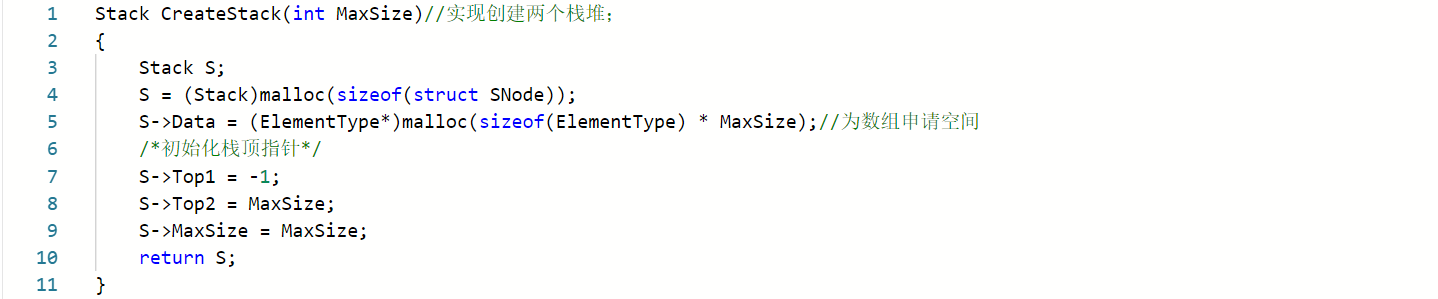
-
把元素x放入栈堆tag中
- 思路
bool Push(Stack s,Elemtype x, int tag)//把x放入栈堆tag中;
{
判断该共享栈是否满了,如果满了就返回false说明入栈失败;
if(tag==1)
进栈1;
else
进栈2;
返回true说明入栈成功;
}
-
代码实现:

-
把栈堆tag中的栈顶删除
- 思路
Elemtype Pop(Stack s,int tag)
{
if(tag==1)//栈1
{
if(s->top1==-1)//栈1为空
返回ERROR说明栈1为空;
else
移动栈顶指针top1,并返回被删除的数据;
}
else //栈2
{
if(s->top2==S->MaxSize)//栈2为空
返回ERROR说明栈2为空;
else
移动栈顶指针top2,并返回被删除的数据
}
}
- 代码实现:

4.C++类模板:stack
stack(堆栈) 是一个容器类的改编,为程序员提供了堆栈的全部功能,也就是说实现了一个先进后出(FILO)的数据结构,以下这些函数可以帮助我们实现上面那些栈的基本操作,我们后续使用栈时就可以直接利用这个stack模板。
头文件 #include <stack>
stack <Elemtype> s;初始化栈,保存Elemtype类型的数据;
s.push(x);入栈元素t;
s.top();返回栈顶指针;
s.pop();出栈操作,只做删除栈顶元素的操作,不返回该删除元素;
s.empty();判断是否栈空,如果为空返回true;
s.size();返回栈中元素个数;
5.栈的应用
- 5.1符号配对
- 思路
这里可以结合map容器,将左右括号进行配对;
- 思路
使用map容器将符号进行配对;
while(str[i])
{
if(str[i]==左括号)
s.push(str[i])//左括号进栈;
else if(str[i]==右括号)
{
if(s.empty())//栈空;
缺少左括号,不匹配,退出循环;
else
{
if(左右括号匹配)
s.pop();//弹出栈顶元素
else//不匹配
退出循环;
}
}
读取下一字符;
}
-
代码实现



-
5.2表达式转换
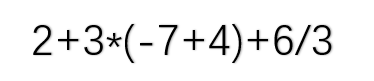
在上学期的学习中我们也曾经接触过表达式求值,但是当时我们做的是不考虑运算符的优先级,直接从左往右进行运算,总体来说难度比较简单(相关题目参见6-6 jmu-c-计算表达式)。而这次我们需要考虑运算符的优先级,还加入了对括号,正负数的判断。直接进行运算难度稍大,因为我们不知道应该从哪里开始运算, 所以我们要先将表达式进行转换,转换成计算机比较容易实现运算的式子————后缀表达式,然后再开始进行运算。- 思路
我们平常遇到的表达式都是 运算符在操作数中间,这种表达式叫做中缀表达式,如果计算机要跳过数据去判断所有运算符的优先级,再按顺序取运算符两边的数据进行运算的话,对计算机来说工作量是很大的。于是如果我们能把运算符的优先级先排好,然后直接取该运算符的前两个数据运算,这样就使得运算变的简便起来。像这样 运算符位于两个运算数之后的表达式式叫做后缀表达式。
我们可以设置一个栈来保存运算符,利用运算符的优先级来进行运算符进栈入栈的操作。这里我们可以用到map容器,对运算符进行赋值,以此来判断栈内栈外运算符优先级的高低。
- 思路
结合运算符优先级用map容器给运算符赋值;
mp<char,int>top;//用于映射已入栈运算符的优先级;
mp<char,int>ex;//用于映射未入栈时运算符优先级;
while(str[i])
{
if(str[i]为数字或者小数点'.')
while(str[i]为数字或者小数点'.')
str[i]写入后缀表达式中,继续读取下一字符;
else if(str[i]为正负号)
将负号写入后缀表达式中,读取下一字符;
else//都是运算符
{
if(栈空 || 栈顶运算符的优先级比str[i]低)
str[i]进栈,再读取下一字符;
else if(栈顶运算符的优先级比str[i]高)
while(栈顶运算符的优先级比str[i]高)
将栈顶元素写入后缀表达式,读取下一字符;
else //栈顶运算符的优先级等于str[i]的优先级,说明是左右括号配对的情况;
将栈顶元素'('出栈;读取下一字符;
}
如果栈不空,则出栈所有元素,写入后缀表达式中;
}
-
代码实现


-
5.3迷宫求解(回溯法)
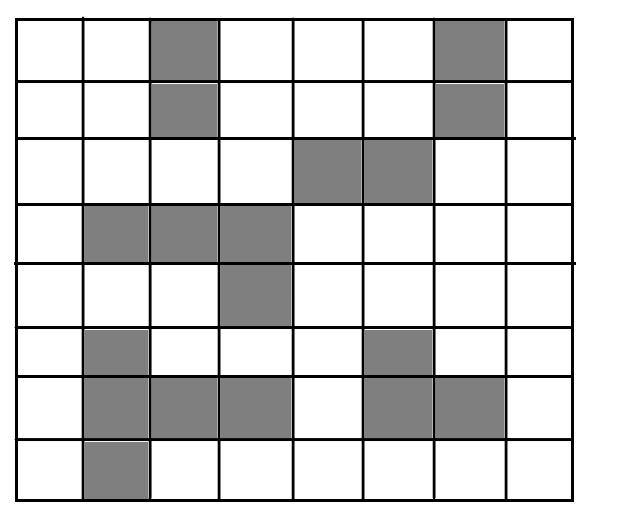
-
思路
首先我们要先把迷宫保存起来,我们可以运用一个二维数组,用数字1表示不可走,数字0表示可走,将方块保存起来,因为在数组中下标是从0开始的,在实际情况中坐标为(1,1)的方块,保存到数组,其位置为(0,0)。所以为了操作方便,我们在迷宫的外围再加上一圈不可走的方块,以便接下来的操作。
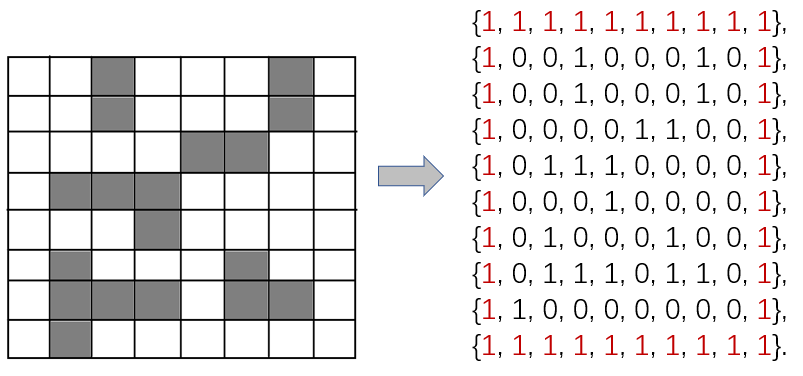
从起点开始,向四周寻找可走方块,只要找到一个可走方块就进栈。然后取栈顶,继续找该方块的下一可走方块,如果该方块没有下一可走方块,就使该方块退栈,返回到上一方块继续找下一可走方块(回溯法)。
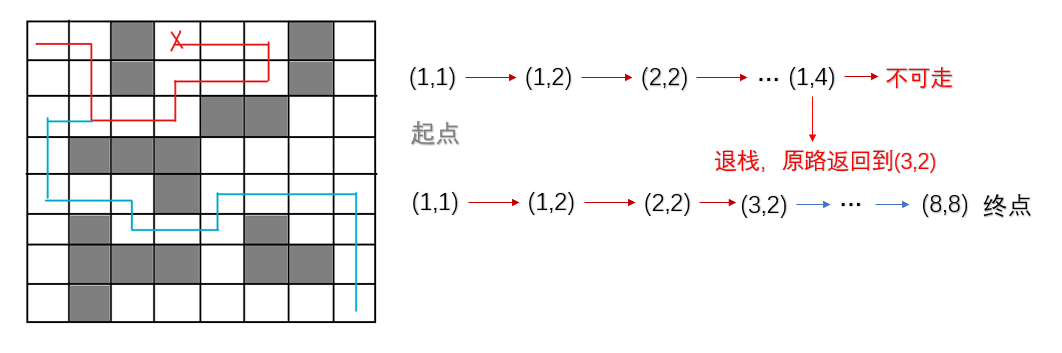
-
伪代码
-
起点坐标先进栈st;
while(st.top>-1)//栈不为空
{
取栈顶坐标;
if(为终点)
输出路径;退出函数;
while(寻找下一可走方块)
找到下一可走方块,将该方块进栈,退出循环;
if(没有找到下一可走方块)
将当前的方块退栈
}
如果退出循环还未找到终点,那么该迷宫无解。
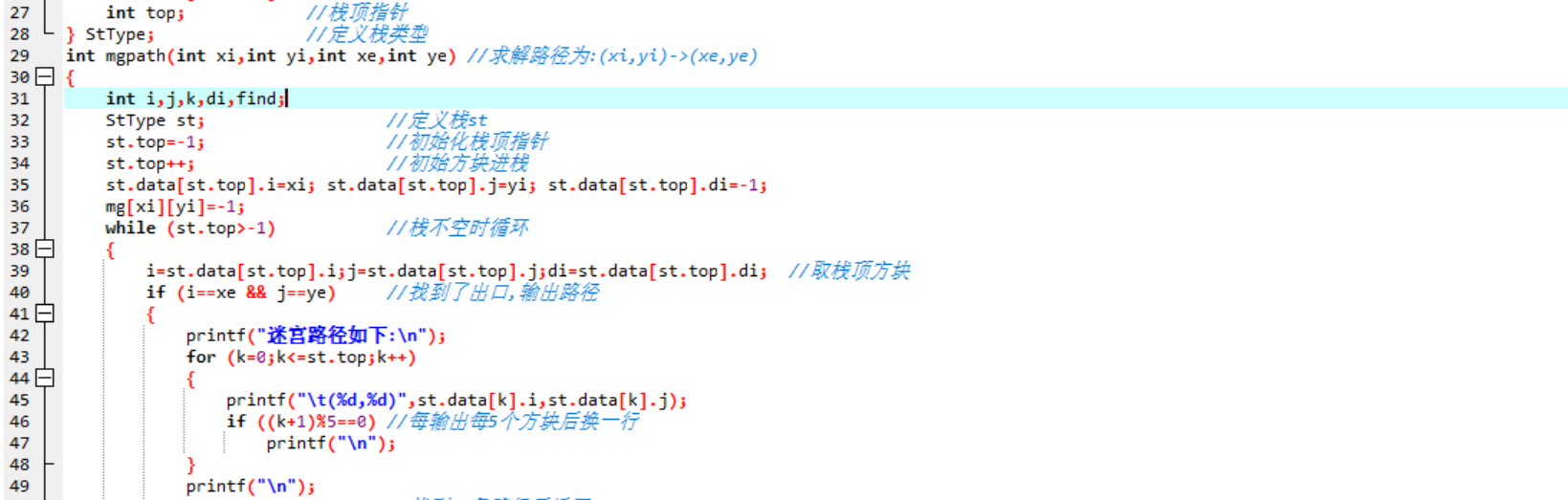
- **代码**



- 结果
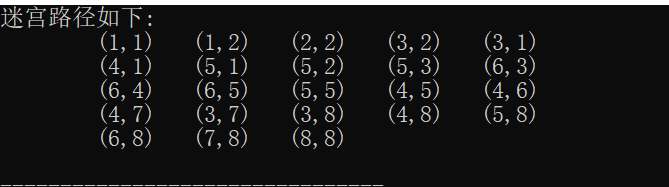
输出迷宫的某条路径(可能不是最短路径),栈实现迷宫的操作是一种深度优先搜索法,他可以找到所有的可能路径。
队列
队列也是一个运算受限的线性表,它只能选取一端进行插入操作,另一端做删除操作,是先进先出的一种结构。我们把进行删除的一段叫做队头,进行插入的一端叫做队尾。
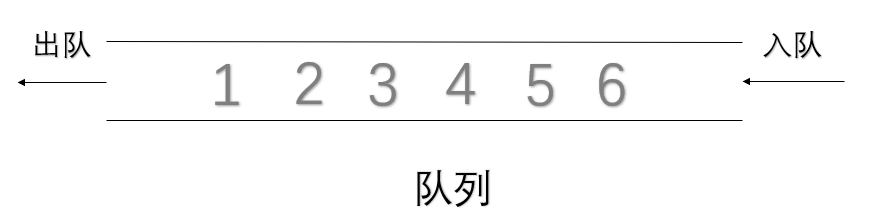
1.队列的存储结构
分为顺序存储结构和链式存储结构,顺序存储结构的队列叫做顺序队,链式存储结构的队列叫做链队。链队中,队头指针和队尾指针是单独放在一个结构体当中。
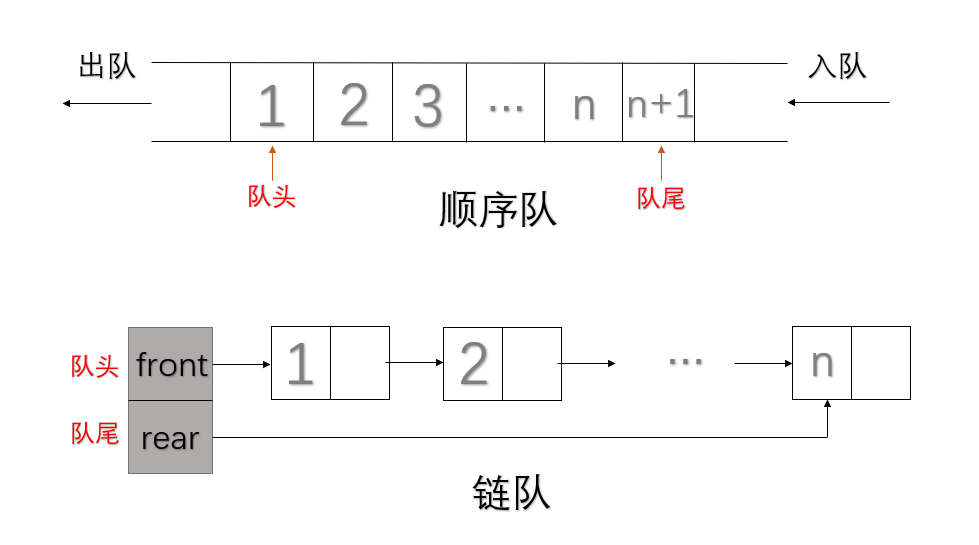
结构体定义
/*顺序队*/
typedf struct
{
Elemtype data[MaxSize];
int front;//队头指针;
int rear;//队尾指针;
}QNode;
/*链队*/
typedef struct qnode//用于保存每个结点;
{
Elemtype data;
struct qnode *next;
}Node,*LinkNode;
typedef struct
{
LinkNode front;//队头指针;
LinkNode rear;//队尾指针;
}Queue;
2.队列的基本操作
- 初始化队列
/*顺序队*/
void InitQueue(Queue &q)
{
q.front=q.rear=-1;
}
/*链队*/
void InitQueue(Queue &q)
{
q.front->next = NULL;
q.rear->next = NULL;
}
- 判断是否为空队
/*顺序队*/
bool IsEmpty(Queue &q)
{
if(q.rear==q.front)//队空
return true;
else//队不空
return false;
}
/*链队*/
bool IsEmpty(Queue &q)
{
if(q.front->next==NULL)//队空
return true;
else
return false;
}
- 判断是否队满
/*顺序队*/
bool IsFull(Queue &q)
{
if(q.rear==MaxSize-1)//队满
return true;
else
return false;
}
/*链队*/
因为是链式存储结构,不用预先设定需要多少的存储空间来保存数据,都是现用现配,空间利用效率比较高。所以只要一个数据我们就可以直接进队,不必考虑是否会队满。
- 进队
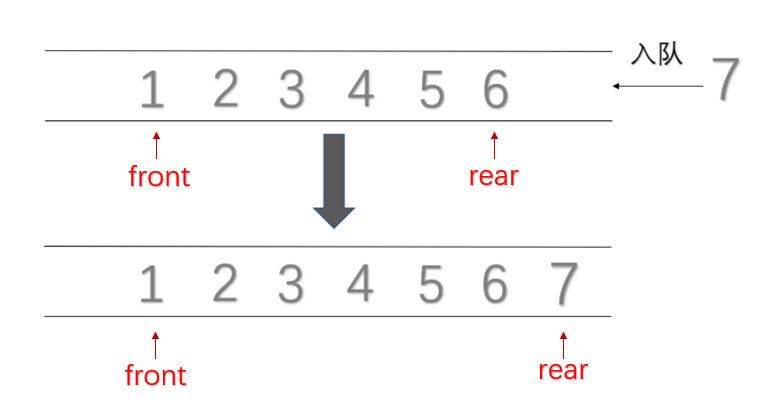
/*顺序队*/
bool Push(Queue &q,Elemtype e)
{
if(IsFull(q))//在进队之前一定要先判断是否队满;
return false;//表示入队失败;
else
q.data[++q.rear] = e;
return true;//表示入队成功;
}
/*链队*/
void Push(Queue &q,Elemtype e)
{
LinkNode qtr;
qtr->data=e;
qtr->next=NULL;
if(IsEmpty(q))//先判断是否为空栈,如果为空栈要对队头指针一起修改;
q.front->next = qtr;
q.rear->next = qtr;
q.rear = qtr;
}
- 取队头元素
/*顺序队*/
bool GetFront(Queue q,Elemtype &e)
{
if(IsEmpty(q))//取队头是要判断是否为空队;
return false;
else
e = q.data[q.front + 1];
return true;
}
/*链队*/
bool GetFront(Queue q.Elemtype &e)
{
if(IsEmpty(q))//取队头要先判断是否为空栈;
return false;
else
e= q.front->next->data;
return true;
}
- 出队
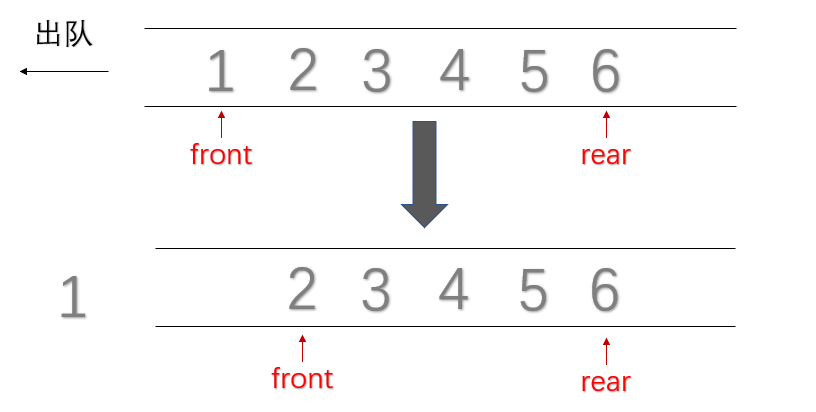
bool Pop(Queue &q,Elemtype &e)
{
if(IsEmpty())//出栈是要先判断是否为空栈;
return false;
else
e = q.data[++q.front];
return true;//表示出队成功;
}
/*链队*/
bool Pop(Queue &q,Elentype &e)
{
LinkNode qtr;
if(IsEmpty())
return false;
else
{
qtr=q.front->next;//先用qtr保存要出队的结点;
q.front->next=qtr->next;//修改队头指针;
e = qtr->data;
delete qtr;//删除结点;
}
}
- 销毁队列
/*顺序栈*/
void DestroyQueue(Queue &q)
{
delete q;
}
/*链栈*/
void DestroyQueue(Queue &q)
{
LinkNode qtr;
while(q.front!=NULL)
{
qtr = q.front;//str保存当前删除的结点
q.front = q.front->next;//s指向下一个需要删除的结点;
delete qtr;
}
}
3.循环队列
由于队列进行插入和删除的操作不在同一端口进行,所以在顺序链中,当队尾指针rear指向数组的最后一个位置作时,存在队头指针front不在数组的第一个位置上,也就是front!=0,队中还存在若干空位置,这种情况我们称为假溢出。所以,为了提高空间的利用率,我们引入一个特殊的队列————循环队列。

结构体定义
/*和顺序表一样*/
typedef struct
{
Elemtype data[MaxSize];
int front;
int rear;
}Queue;
基本操作
- 初始化队列
void InitQueue(Queue &q)
{
front = rear = 0;//指向0位置;
}
- 是否队空
bool IsEmpty(Queue &q)
{
if(front == rear)
return true;
else
return false;
}
- 是否队满
由于循环队列的结构的特殊性,队空和队满的条件都为“ rear==front ”,所以我们在设置循环队列时约定,少用一个空间来判断是否为队满,也就是说,在只剩最后一个空间时,我们不对该空间进行插入操作,而是作为一个队满的标志————“(rear+1)%MaxSize == front”,这样才不会和判断队空的条件重复。

bool IsFull(Queue &q)
{
if((q.rear+1)%MaxSize == q.front)
return true;
else
return false;
}
- 入队
bool Push(Queue &q, Elemtype e)
{
if(IsFull(q))//先判断是否队满;
return false;
else
{
q.data[q.rear] = e;//先保存e,再移动rear指针,所以操作完的rear指针指向的是下一个需要插入的位置,也就是队尾元素的下一个位置。
q.rear = (q.rear+1)%MaxSize;
}
return true;
}
- 出队
bool Pop(Queueu &q, Elemtype &e)
{
if(IsEmpty(q))
return false;
else
e = q.data[q.front];
q.front = (q.front+1)%MaxSize;//操作完的front指向的是队头元素。
}
4.c++容器:queue
该容器是一种链队列的存储结构,所以在执行pop函数时,里面的元素会被删除且释放该元素所在空间
头文件:#include <queue>
q.push(x);将x插入到队列末端,成为新的队尾元素;
q.pop();弹出队列的第一个元素,注意!!这里不返回被弹出元素;
q.front();返回队头元素;
q.back();返回队尾元素;
q.empty();当队空是,返回true;
q.size();返回队列的元素个数;
5.队列的应用
- 5.1报数游戏
报数游戏是这样的:有n个人围成一圈,按顺序从1到n编好号。从第一个人开始报数,报到m(m<n)的人退出圈子;下一个人从1开始报数,报到m的人退出圈子。如此下去,直到留下最后一个人。其中n是初始人数;m是游戏规定的退出位次(保证为小于n的正整数)。(源自:7-6 jmu-报数游戏 ) - 思路
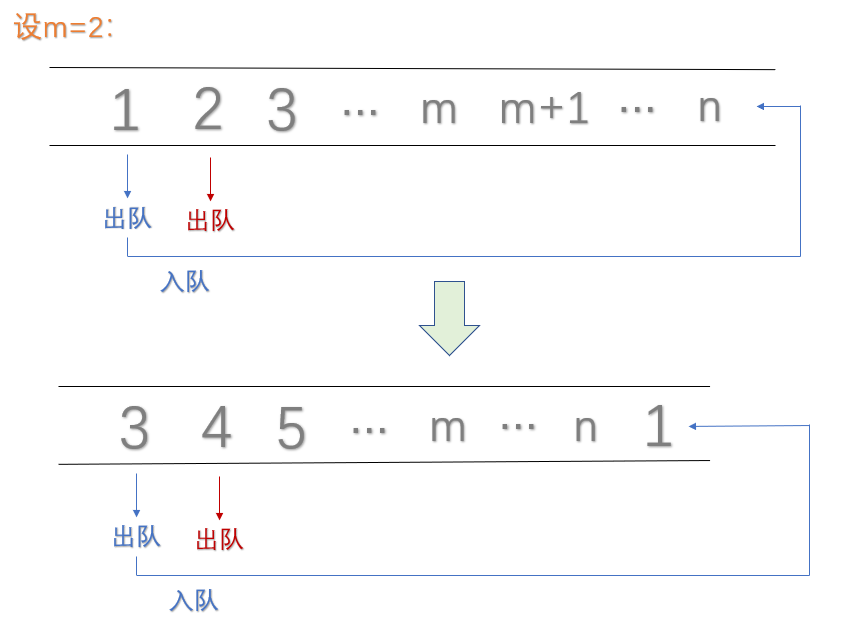
int cout = 0;
while(队不为空)
{
count++;//计数器计数;
if(cout == m)//计数器报到m;
数据出队pop();
count=0;//计数器清零;
else
数据出队pop();
数据再进队push(data);
}
-
代码实现


-
5.2队列实现迷宫(寻找最短路径)
例题:7-8 电路布线
给出m*n个方格,并给出起点和终点,找到最短路径,求其最短路径的长度。 -
思路

先初始化迷宫,然后从起点开始,寻找所有的可走路径,把这个迷宫中所有可走路径都先保存起来,相当于一个树杈图。每一个点的下一步可走点全部都被保存且可继续开发。因为每一条路中的第n步路都是同时进行开发的,当有一条路最先走到终点,即可以证明这条路是最短路径。
typedef struct
{
int i,j;
int num;//用于记录这是第几条路径;
}Box;
void FindRoad(int stari,int straj,int endi,int endj)//stari和starj是起点坐标,endi和endj是终点坐标;
{
Box e,temp;
定义变量many来保存总路径条数,初始化为1;
定义变量len=1来记录步数,初始化为1;
queue<Box>q;//定义队列q;
e.i=stari;e.j=starj;e.num=1;//起点进栈;
q.push(e);
while(!q.empty())
e=q.front();//取队头方块;
for(i=0;i<4;i++)//遍历当前方块的四个方向寻找所有下一可走方块;
向四个方向寻找可走方块;
if(map[i][j]==0)//可走方块;
if i==endi&&j==endj //找到终点
退出;
end if
/*没有找到方块*/
temp.i=i;temp.j=j;temp.num=k;//方块进栈;
q.push(temp);
k++;//方块e总共有几个可走方向;
end if
end for
if 找到终点
len++;
break;
end if
if (many==e.num)//说明当前所有路径都走过了,应该继续往下开发
many=k-1;
k=1;
len++;
end if
end while
}
-
代码实现




-
结果
使用队列实现迷宫求解,得到的路径是最短路径,是一种广度优先搜索法。
课堂拓展
- map容器
- 头文件:
#include <map> - 功能:自动建立key-value的对应,key和value可以是任何你需要的类型;
- 使用:
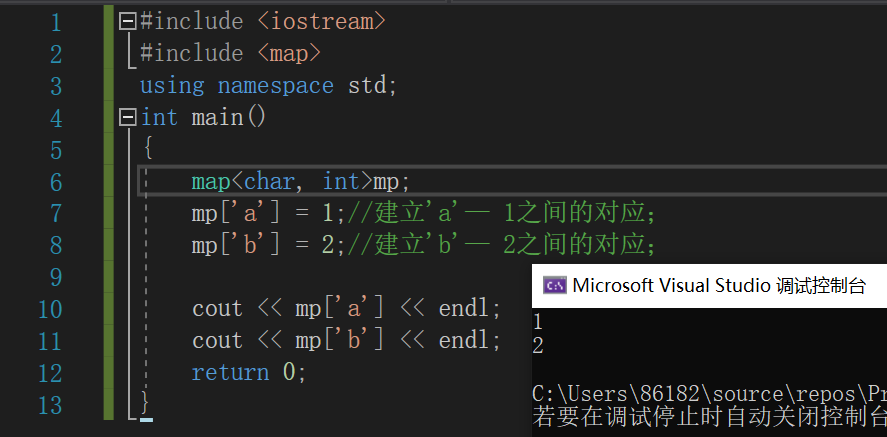
当我们面对某些复杂且不太好处理的数据时,我们可以使用map容器来对这些数据设置一个我们容易识别的标签,比如上面的符号配对还有表达式运算等,如果我们之间对每个符号进行处理,代码量将会非常大。使用map容器建立符号之间的联系会减轻我们许多负担;
- 头文件:
1.2学习体会
难 是真的难。不知道你们是否体验过,在学习的时候想要画出重点来提醒自己加深记忆,却不知不觉整本课本上的内容都几乎被你贴上了重点标签。我在学习栈和队列的时候就是这种心情(TAT:怎么感觉都是重点,不管了全都画起来吧)。其实理解栈和队列的结构不难,要如何灵活运用栈和队列才是真的不容易。比如在队列的报数游戏中,我起初的思路是运用一个链表,在链表内对为m的倍数的编号进行删除操作,遍历到最后一个数字时,再回到链头,继续删除,想法及其之复杂(这还是在我刚学完队列之后。队列:来呀一起快活啊~。我:不,我对你不熟。)。对于学习完的知识还不能学以致用,这是我近期需要克服的一个难题。对于不熟悉的知识还是要继续努力熟悉。学习了栈和队列以后感觉对线性表的了解更深了一些,也发觉到现在的知识是越来越难,题目越来越有挑战性,但不管怎么样,还是要静下心来,脚踏实地,认真学习!
2.PTA实验作业
2.1 7-4 符号配对
2.1.1代码截图



2.1.2本题PTA提交列表说明
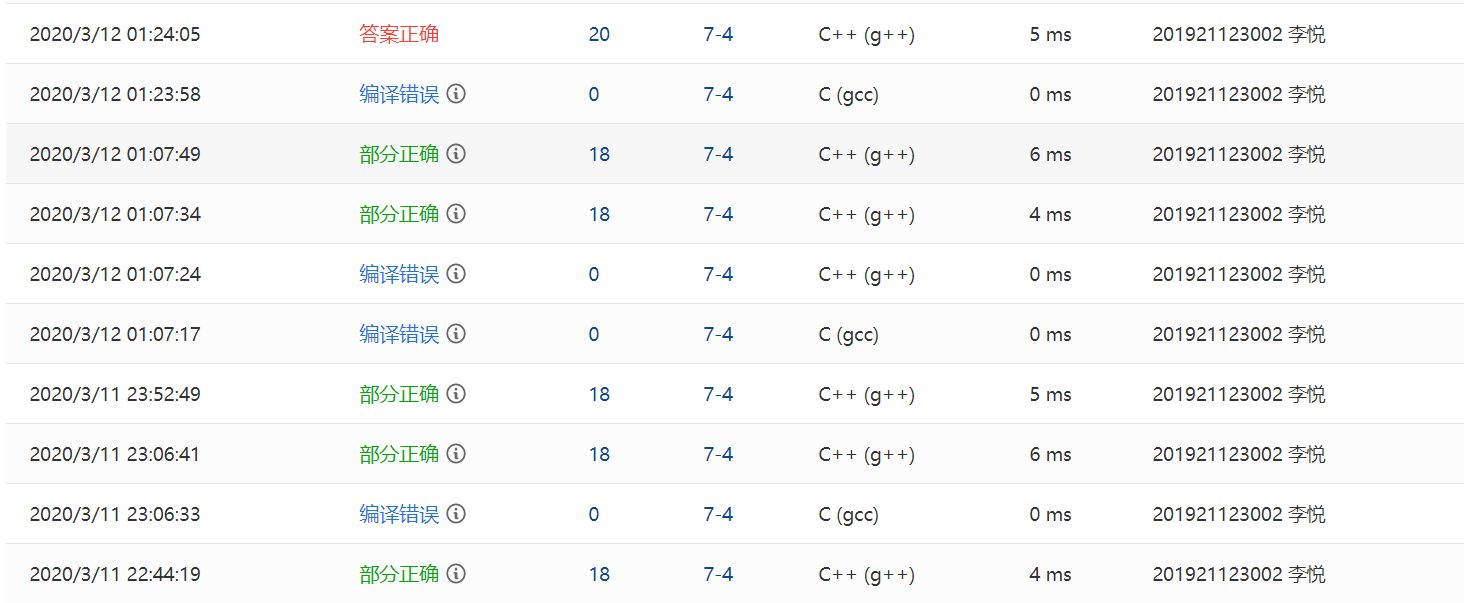
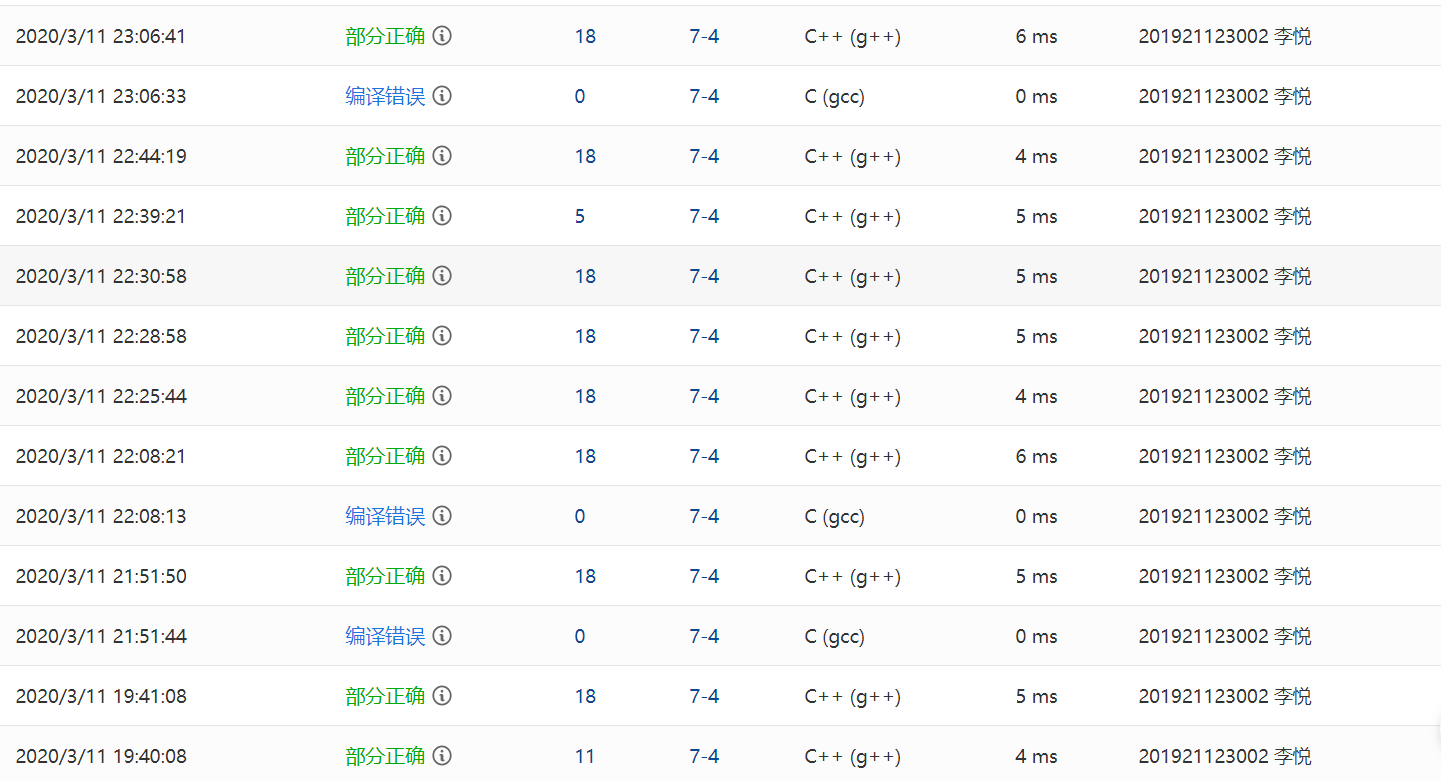
1.编译错误:没有切换到c++语言;
2.部分正确(11分):缺左括号的测试点格式错误,多打了一个空格。还有最后一个测试点未过。
3.部分正确(18分):最后一个测试点未过,刚开始我一直认为只有一个错误点,但其实我犯了两个错误:第一个是结束符标志没有判断清除,题目是说某行只有’.’和回车才结束,也就是说如果有其他符号就不结束,而我只判断了’.’号,遇到’.’就会立马结束。第二个错误是我对注释符的处理没有处理好,在遇到右注释符的时候,我没有进行下移操作,也就是说我判断了右注释符’*’后没有把’/’一起处理,下一次就会遍历到’/’,如果我遇到两个右注释符的时候就会出错,会把第一个右注释符的’/’和第二个右注释符’*’一起配对变成左注释符,导致判断错误。我有这么多的18分是因为我忽略了第二个错误,一直对结束符进行判断。后来才发现原来还有一个错误。
2.2银行排队问题之单窗口“夹塞”版
2.2.1代码截图




2.2.2本题PTA提交列表说明
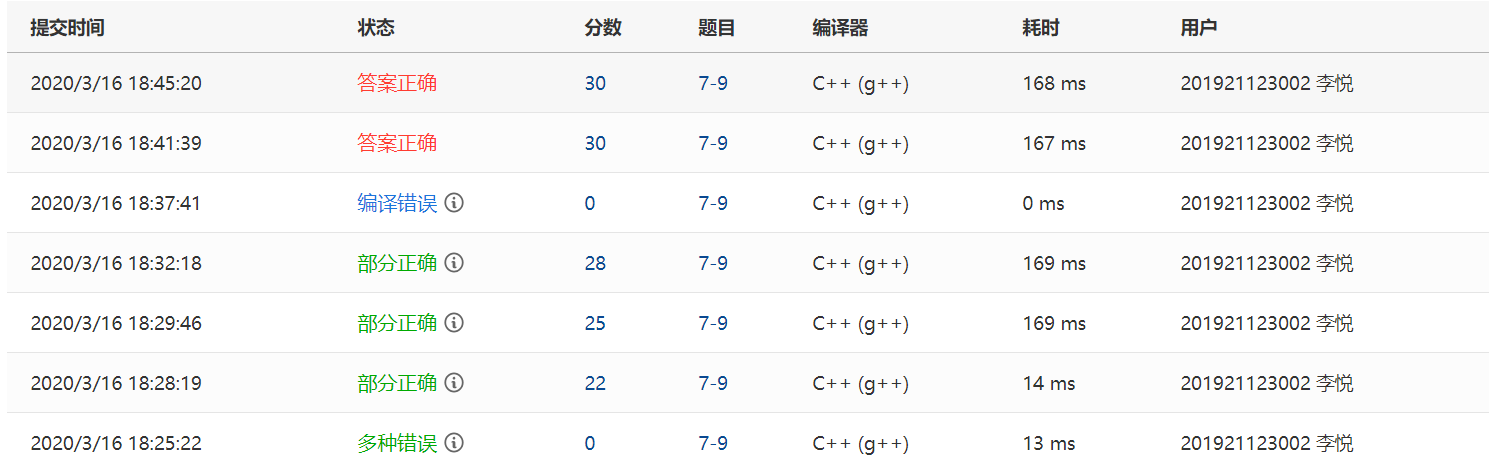
1.多种错误:没有输出顾客的名字;
2.部分正确(22分):最多数据应该有10000,我定义可保存的最大数据只有1000个;
3.部分正确(25分):当某顾客刚好处理完他的朋友就来了,这个时候该顾客会帮朋友处理,而我做的是不处理操作;
4.部分正确(28分):缺少对窗口空闲状态的处理,如果窗口空闲,那么下一位顾客的等待时间就为0,且时钟的值也要改变到下一位顾客到达的时间。
3.阅读代码
3.1 题目及解题代码
- 题目
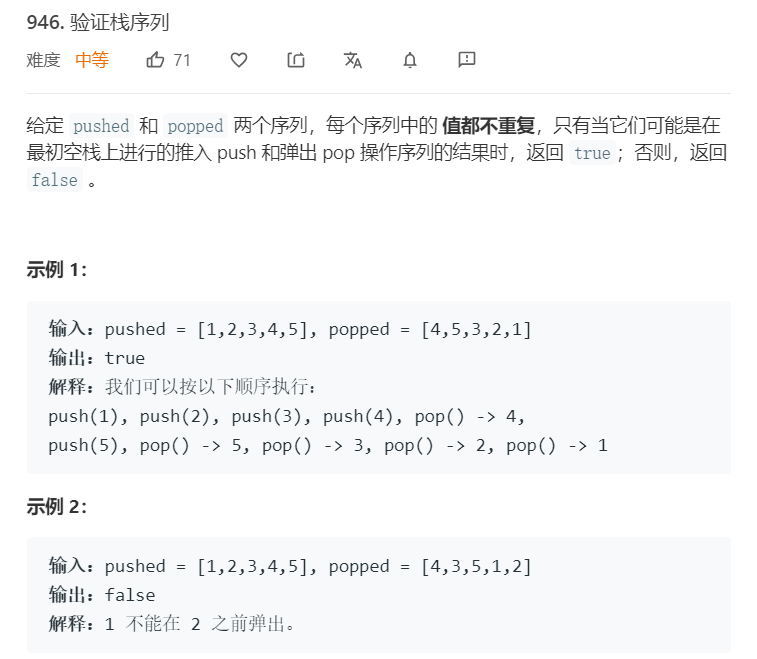
- 代码
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
int n=popped.size(); /*获取序列的大小*/
stack<int> s;
int k=0;
int test=0;
for(int i=0;i<n;i++)
{
s.push(pushed[i]);
/*三个条件的顺序很重要*/
while((!s.empty())&&(k<n)&&(s.top()==popped[k]))
{
s.pop();
k++;
}
}
if(!s.empty()) /*如果非空,则返回false*/
{
return false;
}
return true;
}
};
作者:anisluo
链接:https://leetcode-cn.com/problems/validate-stack-sequences/solution/yan-zheng-zhan-xu-lie-by-anisluo/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.1.1 该题的设计思路
1.引入一个栈stack
2.把pushed序列按顺序放到栈stack中,每放一个数据对比栈顶与序列popped中元素是否相同,
3.若相同,则栈stack执行pop操作,popped序列移动到下一个元素,继续对比栈顶与该元素是否相同。
4.如果popped中的每个元素都判断完毕,而最后stack不为空,则说明该栈序列不合法,如果为空,则合法;

时间复杂度为:O(n)(n为序列的元素个数),最复杂的情况就是当结果为"true"时,每个元素都进栈一次又出栈一次,n个元素都进栈一次出栈一次,所以时间复杂度为O(n);
空间复杂度为: O(n),最坏情况是所有元素都进栈,最后再一个一个出栈,此时在栈中开辟了n个空间保存元素,空间复杂度为O(n);
3.1.2 该题的伪代码
获取popped序列的大小n;
k用于遍历popped序列;
i用于遍历pushed序列;
for(i=0;i<n;i++)
{
先按照给出的进栈序列pushed[k] 按顺序进栈s;
while(!s.empty() && k<n && s.top==poped[k])//如果相等,s中的栈顶元素就出栈;
{
s.pop();
k++;//继续遍历popped的下一个元素;
}
}
判断栈是否为空,如果栈不为空,说明该出栈序列不正确;
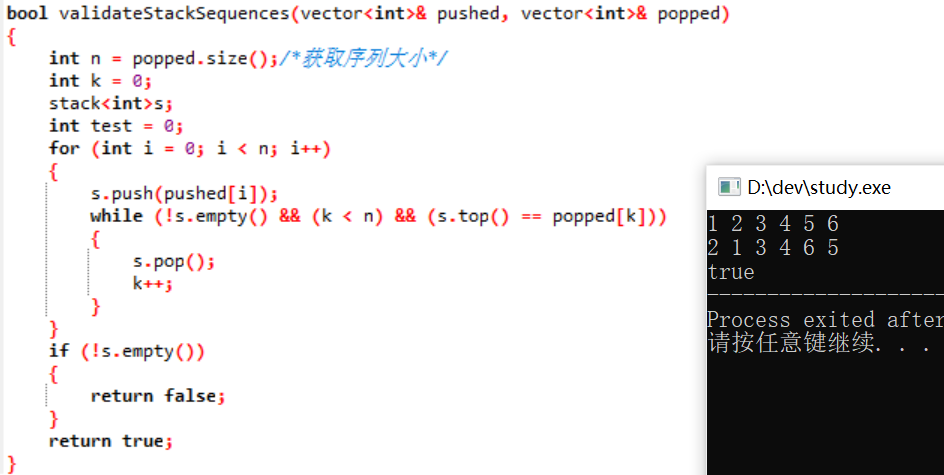
3.1.3 运行结果
3.1.4分析该题目解题优势及难点
- 优势:灵活运用了栈的结构特性,方法简单易懂,容易操作,有利于我们巩固栈的知识;
- 难点:严格来说这道题目的难度应该不是很大,但是当我在看到这道题目的时候,一瞬间无法联系起栈的结构特性,脑子里面想的是要如何直接判断顺序不合法,是不是要找到出栈元素在原进栈序列中的位置,然后和前面已经出栈的元素在原进栈序列中的位置进行比较什么什么之类的,完全没有什么头绪。看到题解的时候真真切切的感受到了挫败,发现自己其实对该章的知识点了解的还是不透彻,如果能完全掌握栈的知识点及其结构特性,这道题目应该是没有难度的。
3.2 题目及解题代码

class MaxQueue {
queue<int> q;
deque<int> d;
public:
MaxQueue() {
}
int max_value() {
if (d.empty())
return -1;
return d.front();
}
void push_back(int value) {
while (!d.empty() && d.back() < value) {
d.pop_back();
}
d.push_back(value);
q.push(value);
}
int pop_front() {
if (q.empty())
return -1;
int ans = q.front();
if (ans == d.front()) {
d.pop_front();
}
q.pop();
return ans;
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/dui-lie-de-zui-da-zhi-lcof/solution/mian-shi-ti-59-ii-dui-lie-de-zui-da-zhi-by-leetcod/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2.1 该题的设计思路
- 当一个元素进入队列的时候,它前面所有比它小的元素就不会再对最大值的答案产生影响

- 所以我们可以引入一个双端链表来保存一个单调递减的序列,用于维护最大值。
如何实现构造一个单调递降序列,我们只需要在插入每一个元素 value 时,从队列尾部依次取出比当前元素 value 小的元素,直到遇到一个比当前元素大的元素再停下,然后把value从队尾插入进去。这里我们需要引入一个新的队列,双端队列,双端队列可以在两端进行插入和删除。
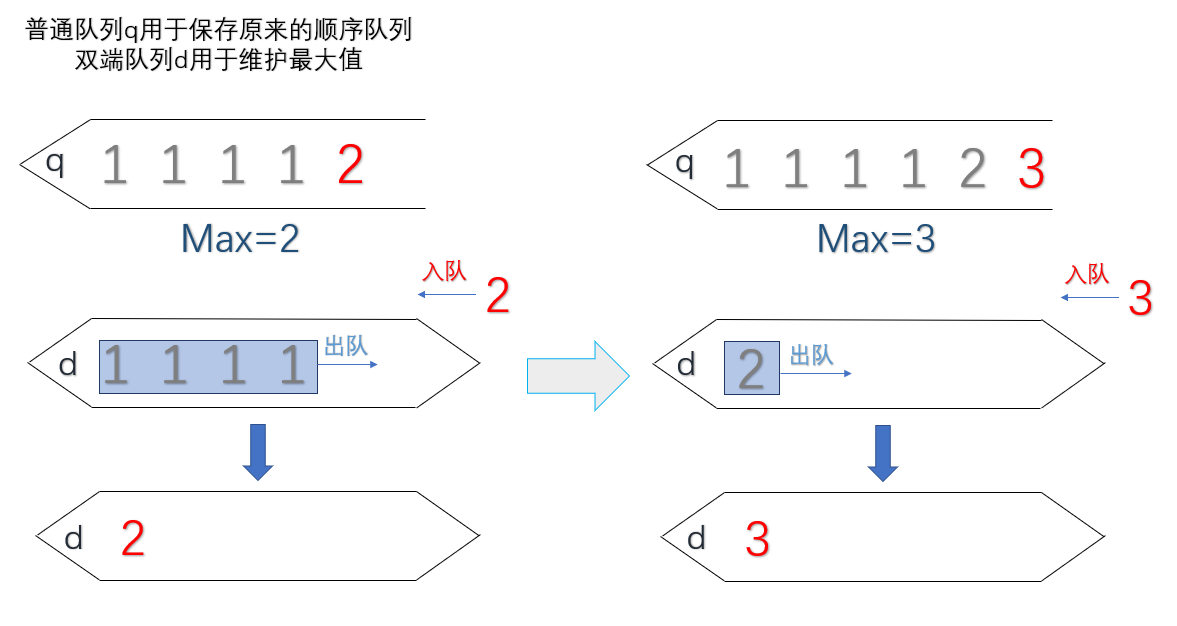
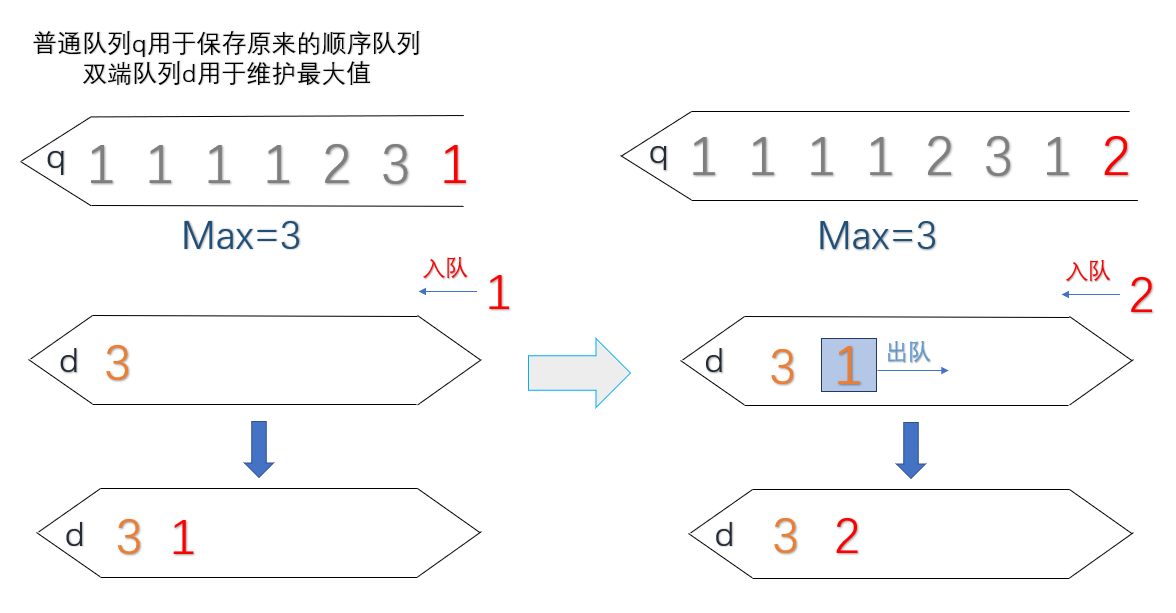
- 时间复杂度:O(1),这里指的是均摊后的时间复杂度(就是计算每一次操作的复杂时间),可以理解成一个元素本来都进行出队又进队的操作(时间复杂对为O(1))。但是他们并没有立即出队,把出队的时间花的时间先省下来,然后比它们大的元素来了之后再一起出队,时间又补上去。
- 空间复杂度:O(n),需要用队列存储所有插入的元素。
3.2.2 该题的伪代码
int max_value()//找当前最大值;
{
if(d.empty())//说明队列中已经没有元素了
return -1;
return d.front();//双端队列中第一个位置永远是最大值;
}
void push_back(int value)//进队操作;
{
while(要插入的数据value比双端队列中元素大)
{
d.pop_back();//把双端队列中所有比value的元素全部都从队尾出队;
}
d.push_back(value);//把value从队尾插入双端队列中;
q.push(value);//要用q保存原来的进队顺序;
}
int pop_front()//出队
{
if(q.empty())
return -1;//说明队列里面已经没有元素了;
int ans = q.front();//保存出队元素;
if(ans == d.front())//如果出队元素为当前队列中的最大值;
d.pop_front();//要把双端队列中的最大值一起从队头移出,改变当前队列中的最大值
q.pop();//出队;
return ans;
}
3.2.3 运行结果
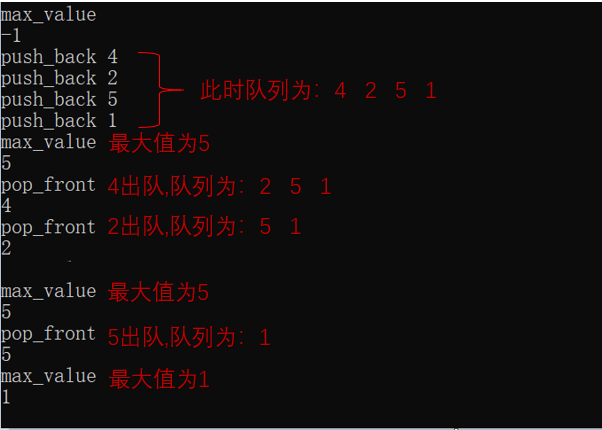
3.2.4分析该题目解题优势及难点
- 优势:寻找队列中最大值,我们一般会想到去遍历队列中所有的元素,然后找到最大值。而这种做法借助了双端队列来实时更新当前队列中的最大值,这样我们就不用每次都去遍历队列,时间复杂度大大降低,方法巧妙。
- 难点:因为对双端队列的不熟悉,所以比较难想到这个方法。如何构造一个单调递减的序列需要结合双端队列可以在两端进行插入删除操作的性质,这里比较不容易想到。还有关于时间复杂度的计算也比较复杂,我一直以为这个的时间复杂度为O(n),但是题目要求要设计一个时间复杂度均摊为O(1)的代码,我又去看了一下题解,绕来绕去还是有点不大清楚。


