机器学习中的评价指标

 

基本概念介绍

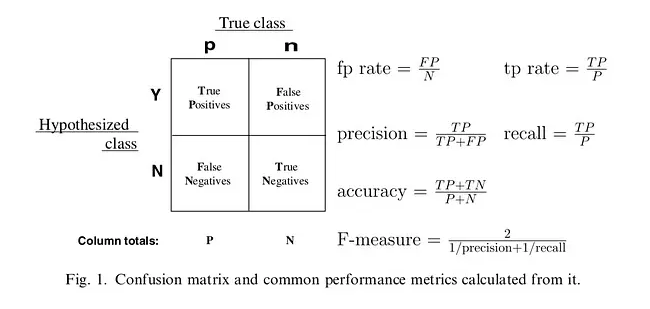
　　1 混淆矩阵

　　　　　　　　　　　　　　

 

 

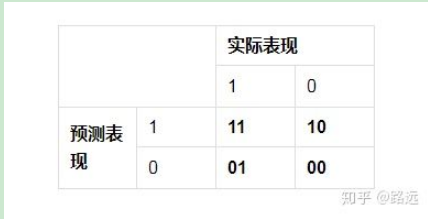
 　　2 　准确率：

　　　　　　　　　　　　　

 

 

 

 

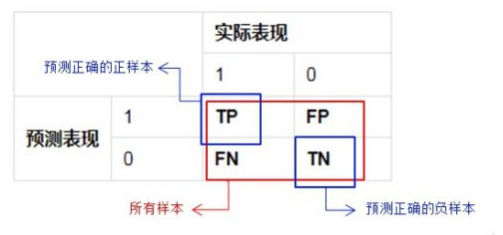
　　 3  精准率：

　　　　　　　　　　

 

 

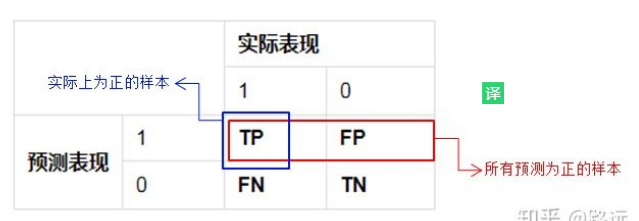
 　　  4 召回率： 

　　　　　　　　　　

　　　 5 P-R曲线(查准率与查全率)

　　　　　　　　　　　　

 

 

 

 

 

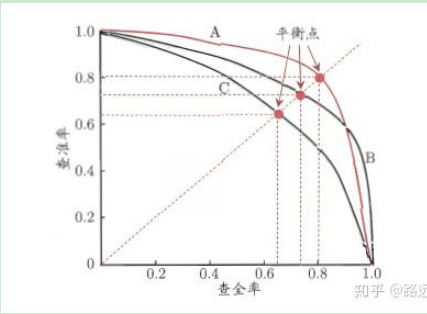
 　　　6  灵敏度与特异度

　　　　　　　　　　

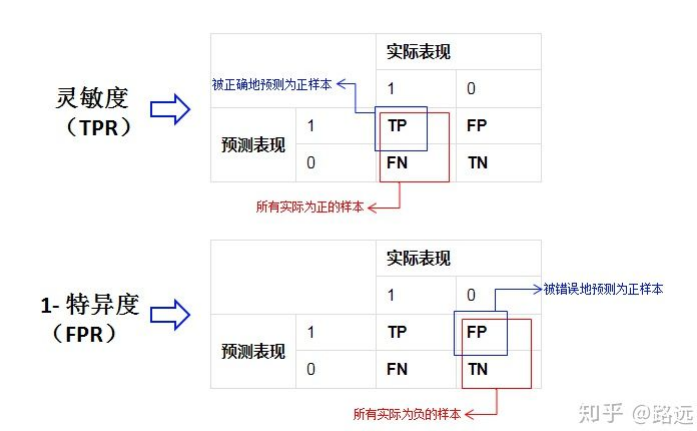
 　　　　概率角度理解评价指标：

　　　　　　　　　　我们也可以从另一个角度考虑：条件概率。我们假设X为预测值，Y为真实值。那么就可以将这些指标按条件概率表示：

　　　　　　　　　　 

 

 

 　　　　　　　　　　

            7 ROC曲线  

　　　　　　　　 TPR: 真正率  FPR：假正率

　　　　　　　　　　

介绍下AUC原理 

由于AUC关联的内容比较多，面试时问得也非常细，因此，我们将按照以下顺序对AUC进行重点介绍。

• 为什么要用AUC？
• AUC与ROC？
• AUC的实际含义及计算方法？

为什么要用AUC？

1. 为什么不用准确率(accuracy)?

在二分类中，如果正反例分布不平衡，而我们对minority class 更感兴趣，这时accuracy评价指标基本没有参考价值，比如欺诈检测，癌症检测等场景。举个栗子：

在测试集里，有100个sample，99个反例，只有1个正例。如果我的模型不分青红皂白对任意一个sample都预测是反例，那么我的模型的accuracy是 正确的个数／总个数 = 99/100 = 99%。

2. 为什么不用召回率(recall)和精确率(precision)?

• 召回率：把实际为真值的判断为真值的概率。

• 精确率：判断为真值，判断正确的概率（实际也为真值）。

• recall = TP / (TP + FN)

• precision = TP / (TP + FP)

一般说来，如果想要召回的多，精确率就要下降；想要精确率提升，召回的就少。因此，召回率与精确率是鱼与熊掌不可兼得。

3. 为什么不用F1分数？

F1-score 可以看做是precision和recall的综合评价指标，公式为：

 

 

 

问题就是，如果你的两个模型，一个precision特别高，recall特别低，而另一个recall特别高，precision特别低的时候，F1-score可能是差不多的，你也不能基于此来作出选择。

4. AUC适用场景

说到这里，终于讲到我们的AUC了，它是一个用来评估分类模型性能的常见指标，优点是：

• 适用于正负样本分布不一致的场景； 在负样本数量远远大于正样本数量的情况下，PR曲线更能反映分类器的好坏
• 对于分类器性能的评价，不限定单一的分类阈值；

不过，要真正理解地AUC，还要从ROC开始讲起。

 

 

 

 

AUC与ROC？

ROC是什么？

ROC，全名叫做Receiver Operating Characteristic（受试者操作曲线），其主要分析工具是一个画在二维平面上的曲线——ROC curve，其中，平面的横坐标是假正率（FPR），纵坐标是真正率(TPR)。

几个概念简单解释下：

• 真正率(TPR) = 灵敏度(Sensitivity) = 召回率：把实际为真值的判断为真值的概率。
• 特异度(Specificity)：把实际为假值的判断为假值的概率。
• 假正率(FPR) = 1 - 特异度：把实际为假值的判断为真值的概率。

• TPR = TP / (TP+FN)

• FPR = FP / (FP + TN

ROC曲线就是，在测试样本上根据不同的分类器阈值，计算出一系列的（FPR,TPR）点集，将其在平面图中连接成曲线，这就是ROC曲线。

画roc曲线的一个例子

假设已经得出一系列样本被划分为正类的概率，然后按照大小排序，下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

 

 

 

 

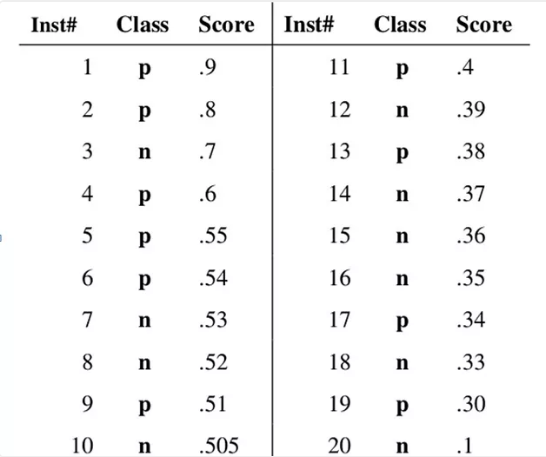
接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

 

进一步理解ROC曲线

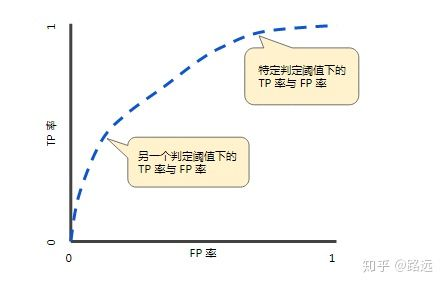
如下面这幅图，(a)图中实线为ROC曲线，线上每个点对应一个分类器阈值下(FPR,TPR)。

 

 

 

 

 

 

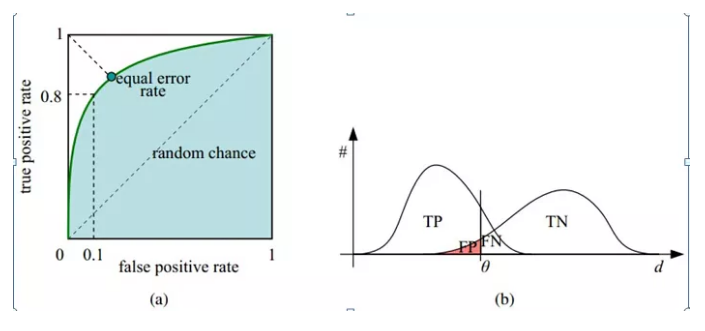
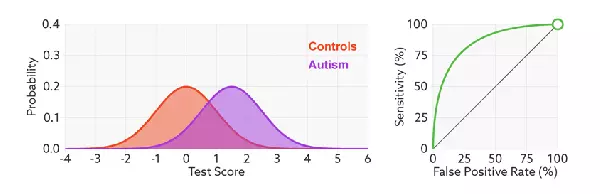
横轴表示FPR，FPR越大，预测正类中实际负类越多。

纵轴表示TPR：正类覆盖率，TPR越大，预测正类中实际正类越多。

ROC曲线必过(0, 0)和(1, 1)两个点。

• (1, 1)点含义：判分阈值为0，所有样本都被预测为正样本，TPR=1，FPR=1。
• 判分阈值逐渐增加，TPR和FPR同时减小。
• (0, 0)点含义：判分阈值为1，所有样本都预测为负样本，TPR=0，FPR=0。

理想目标：TPR=1，FPR=0，即图中(0,1)点，故ROC曲线越靠拢(0,1)点，越偏离45度对角线越好，Sensitivity、Specificity越大效果越好。

AUC与ROC的联系

虽然，ROC曲线可以评测分类器的好坏，但是，人们总是希望能有一个具体数值来作为评价指标，于是Area Under roc Curve(AUC)就出现了。

顾名思义，AUC的值就是处于ROC curve下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的performance。

AUC怎么计算？

AUC有什么实际含义呢？简单来说其实就是，随机抽出一对样本（一个正样本，一个负样本），然后用训练得到的分类器来对这两个样本进行预测，预测得到正样本的概率大于负样本概率的概率，这个概率值就是AUC。

有以下两种方式计算AUC：

（1）方法一：

在有M个正样本,N个负样本的数据集里。一共有M*N对样本（一对样本即，一个正样本与一个负样本）。统计这M*N对样本里，正样本的预测概率大于负样本的预测概率的个数。

计算复杂度：O(M*N)。

（2）方法二：

 

 

 

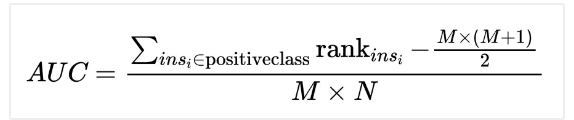
其中：

（1）M, N分别是正样本和负样本的个数；

（2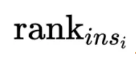）代表第i条样本的序号。（概率得分从小到大排，排在第rank个位置）

（3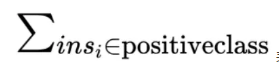）表示把正样本的序号加起来。

AUC的计算主要以下几种方法：

计算ROC曲线下的面积。这是比较直接的一种方法，可以近似计算ROC曲线一个个小梯形的面积。几乎不会用这种方法
从AUC统计意义去计算。所有的正负样本对中，正样本排在负样本前面占样本对数的比例，即这个概率值。
具体的做法就是它也是首先对prob score从大到小排序，然后令最大prob score对应的sample 的rank为n，第二大score对应sample的rank为n-1，以此类推。然后把所有的正类样本的rank相加，再减去M-1种两个正样本组合的情况。得到的就是所有的样本中有多少对正类样本的score大于负类样本的score。最后再除以M×N。公式如下：

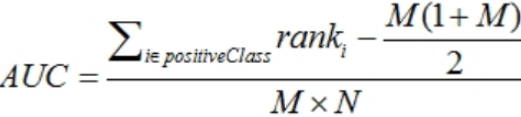
AUC计算代码：

def calAUC(prob,labels):
    f = list(zip(prob,labels))
    rank = [values2 for values1,values2 in sorted(f,key=lambda x:x[0])]
    rankList = [i+1 for i in range(len(rank)) if rank[i]==1]
    posNum = 0
    negNum = 0
    for i in range(len(labels)):
        if(labels[i]==1):
            posNum+=1
        else:
            negNum+=1
    auc = 0
    auc = (sum(rankList)- (posNum*(posNum+1))/2)/(posNum*negNum)
    print(auc)
    return auc

 参考文献：1  https://www.zhihu.com/question/30643044

　　　　　  2 https://mp.weixin.qq.com/s/rfnMox5BEKhrBcpGRMvRVg