(转)一个骰子，6面，1个面是 1， 2个面是2， 3个面是3，问平均掷多少次能使1、2、3都至少出现一次。

 

题目：一个骰子，6面，1个面是 1， 2个面是2， 3个面是3，问平均掷多少次能使1、2、3都至少出现一次。

解法一：（没学过《组合数学》的请略过）

设P（N=n）表示第n次（n>2）抛出后1，2，3都出现的概率，问题要求n的期望E(N=n).掷1的概率p=1/6,掷2的概率q=1/3,掷3的概率r=1/2.

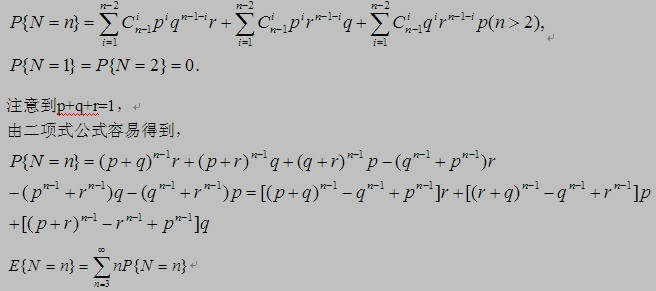
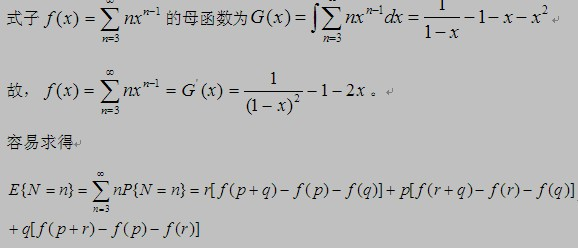
#include <iostream>
using namespace std;
float f(float x)
{
   return (1/(1-x)/(1-x)-1-2*x);
}
 
 
int main()
{
   float p=1.0/6,q=1.0/3,r=1.0/2,e;
   e=r*(f(p+q)-f(p)-f(q))+p*(f(q+r)-f(q)-f(r))+q*(f(p+r)-f(p)-f(r));
   cout<<e<<endl;
   return 0;
}

解法二、 面对面试概率题几乎屡试不爽的分叉树递归列方程法。

这是一个求数学期望的问题，最终是求1，2，3出现至少一次的最短长度的期望。

这样分叉树的每个节点是一个期望状态，而每个分叉是一次投掷结果。将后续期望出现1、2、3各至少一次的情形记作L123（即题目所求），将后续期望出现1、2各至少一次（3无关）情形记作L12，而1至少一次（2，3无关）情形L1，其余数值符号类推，则树结构如下（列出4级结构已经足够）：

第一级（树根）	第二级	第三级	第四级别
L123	掷1->L23	掷1->L23	同状态
		掷2->L3	根据投掷结果，或继续期待L3，或已经达到目标
		掷3->L2	根据投掷结果，或继续期待L2，或已经达到目标
	掷2->L13	掷1->L3	根据投掷结果，或继续期待L3，或已经达到目标
		掷2->L13	同状态
		掷3->L1	根据投掷结果，或继续期待L1，或已经达到目标
	掷3->L12	掷1->L2	根据投掷结果，或继续期待L2，或已经达到目标
		掷2->L1	根据投掷结果，或继续期待L1，或已经达到目标
		掷3->L12	同状态

接下来，就是要排出方程，因为一共7个未知数，如果排出7个线性方程就能解决问题。

这方程组里的未知数对应上述的状态，而其数值则是一个对长度（投掷次数）的数学期望。

根据这个树状结构和其中的递归关系，这个方程组就是：

L123 = p1 (L23+ 1) + p2 (L13+1) + p3 (L12 + 1) = p1 L23 +p2 L13+ p3 L12 + 1

（以这个L123为例，解释，投掷1的概率是p1而由此得到的结果是需要期待后续2和3各至少出现一次，于是长度期望是L23+ 1，加1是因为投掷了一次，亦即即增进一级）

L23 = p1 L23 +p2 L3+ p3 L2 + 1

L13 = p1 L3 +p2 L13+ p3 L1 + 1

L12 = p1 L2 +p2 L1+ p3 L12 + 1

L1 =p2 L1+ p3 L1 + 1

（这里实际上是 L1 =p1 ·1 + p2 (L1+1) + p3 (L1 +1) =p2 L1+ p3 L1 + 1，因为对L1情形，如果投了1就目的达到终止了）

L2 =p1 L2 +  p3 L2 + 1

L3 =p1 L3 +p2 L3+ 1

（以上一开始没注意，多加了悬空的概率项，故计算有误）

其中 p1，p2 和 p3分别是掷出1，2和3的概率，即1/6，1/3，1/2。

于是求解这个方程，得到：

L1 = 6， L2 = 3， L3 = 2

L12 = 7， L13 = 13/2， L23 = 19/5

L123 = 219/30 = 7.3

故以上如果没有计算错误，该题结果是，平均掷7.3次可出现这些面值各至少一次。

解法三、

首先介绍一下指示器随机变量。
指示器随机变量为概率与期望之间的转换提供了一个便利的方法。给定一个样本空间S和事件A，那么事件A对应的指示器随机变量I{A}定义为
I(A)=1 如果A发生的话；0 如果A不发生的话。
首先证明以下结论：
抛N次，123没有全部出现的概率，记为p(n),很容易通过容斥原则求出p(n)。
对p(n)从n=0到无穷求和。即为题目所求的期望。
定义随机变量X_n=1表示事件“前n次投掷骰子,123没能全部出现”发生，X_n=0表示这个事件没发生，即X_n是该事件的指示变量。
令p(n)为“投n次骰子，123没能全部出现”的概率，即X_n的数学期望为：
E[X_n] = 1*Pr[X_n=1]+0*Pr[X_n=0]=p(n)
令随机变量X表示投掷到多少次时，123刚好全部出现过。
最关键的一步是发现一下的恒等关系：
X=X_0+X_1+X_2+X_3+......
即X为所有X_n的和，n=0到无穷。
例如：假设投掷到第7次时123刚好全部出现，即X=7，即X_0到X_6都为1，从X_7开始至n无穷,X_n都为0.
我们的目标是求E[X]，根据期望的线性，有：
E[X] = E[X_0] + E[X_1] + E[X_2] + E[X_3]+...
注意尽管各个X_n之间并不独立，但线性期望对于任何随机变量都是无条件成立的，所以我们总可以轻松吧问题化整为零。
前面已经能够知道E[X_n]=p(n),而且p(n)可以用容斥原理则轻松算出。因此所求期望就是所有p(n)的和，n=0到无穷，这是一个简单的几何级数。
p(n)=(1/2+1/3)^n + (1/2+1/6)^n+(1/3+1/6)^n - (1/2)^n-(1/3)^n-(1/6)^n
=(5/6)^n+(2/3)^n-(1/3)^n-(1/6)^n -----n>0的时候
而p(0) 根据定义应该是1
那么这个答案应该是
而几何级数1+q+q^2+q^3+....=1/(1-q)   因此E[x] = 1 + 6 + 3 - 3/2 - 6/5 = 7.3