斐波那契数列的C语言实现

斐波那契数列

经典数学问题之一；斐波那契数列，又称黄金分割数列，指的是这样一个数列：

  1、1、2、3、5、8、13、21、……

前两个数为1， 1，之后每个数都为为前面两个数的相加。

 

C语言实现：

输出斐波那契数列前n个数字：

1、普通算法

#include <stdio.h>

int test2(void);

int main(void)
{
    while(1)
    {    
        int flag = test2();
        if(flag != 1)    break;
    }
    return 0;
}

int test2(void)
{
    int t1 = 1, t2 = 1, n, next, i;
    
    printf("How many:");
    scanf("%d", &n);
    
    if(n <= 0)
    {
        printf("Program Terminated!\n");
        return -1;
    }
    
    for(i = 1; i <= n; i++)
    {
        printf("%d ", t1);
        next = t1 + t2;
        t1 = t2;
        t2 = next;
    }
    printf("\n");
    return 1;
}

2、递归实现

#include <stdio.h>

int test3(int);
int test5(void);

int main(void)
{
    while(1)
    {    
        int flag = test5();
        if(flag != 1)    break;
    }
    return 0;
}

/* 使用递归方式 */
int test3(int index)
{
    if(index == 1 || index == 2)    return 1;
    return (test3(index -1) + test3(index -2));
}

int test5(void)
{
    int i, n;
    printf("How many:");
    scanf("%d", &n);
    
    if(n <= 0)
    {
        printf("Program Terminated!\n");
        return -1;
    }
    
    for(i = 1; i <= n; i++)    
    {
        printf("%d ", test4(i));
    }
    printf("\n");
    return 1;
}

运行结果：

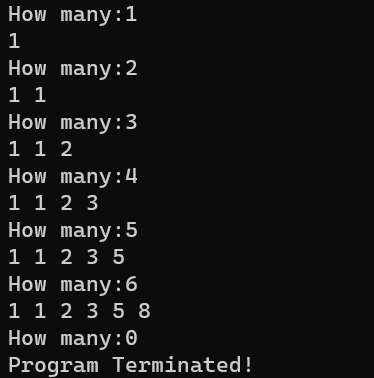
用递归的方法实现此数列简洁，方便理解。但是我们仔细观察上面的代码，就会发现此函数中存在着大量的冗余计算，并且n越大，冗余的越多。

 

输出数列中小于等于Max的数字

#include <stdio.h>

int test6(void);

int main(void)
{
    while(1)
    {    
        int flag = test6();
        if(flag != 1)    break;
    }
    return 0;
}

int test6(void)
{
    int t1  =1, t2 = 1, next, Max;
    
    printf("Max: ");
    scanf("%d", &Max);
    
    if(Max <= 0)
    {
        printf("Program Terminated!\n");
        return -1;
    }
    
    while(t1 <= Max)
    {
        printf("%d ", t1);
        next = t1 + t2;
        t1 = t2;
        t2 = next;
    }
    printf("\n");
    return 1;
}

运行结果：

 

 

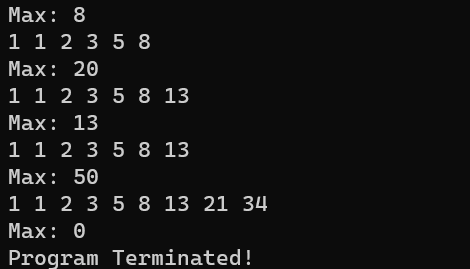
新人才疏学浅，有错的地方敬请指正！！

本文来自博客园，作者：夏末终年，转载请注明出处：https://www.cnblogs.com/xiamozhongnian/p/15861331.html