强化学习总结(4)--蒙特卡洛方法
大名鼎鼎的蒙特卡洛方法(MC),源自于一个赌城的名字,作为一种计算方法,应用领域众多,主要用于求值。蒙特卡洛方法的核心思想就是:模拟---抽样---估值。
蒙特卡洛的使用条件:1.环境是可模拟的;2.只适合情节性任务(episode tasks)。
蒙特卡洛在强化学习中的应用:
1.完美信息博弈:围棋、象棋、国际象棋等。
2.非完全信息博弈:21点、麻将、梭哈等。
前面的动态规划方法,要求环境模型已知,然后根据已知的转移概率,求出所有的状态值和动作,选出其中值函数最高的一些列动作构成最优策略。但MC方法面对的是model-free,依靠经验就可以求解最优策略。
那么,什么是经验呢?经验其实就是训练样本,不管怎么样,对一个任务从头到尾执行一遍,就得到了一个训练样本,如果有大量的样本,那么就可以估计在状态s下,遵循某个策略的期望回报,也就是状态值函数。
这样应该就明白了,MC方法是依靠大量样本的平均回报来解决强化学习问题的。
在正式开始MC之前,先放上一张人神共知的图,看看DP和MC还有后面的TD到底有什么关系。
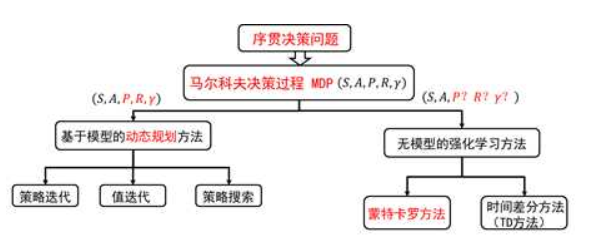
1.MC的基本概念
当我们要评估智能体的当前策略时,可以利用策略产生很多次试验,每次试验都是从任意的初始状态开始直到终止状态,比如一次试验为S1,A1,R2,S2,A2,R3.........,计算一次试验找那个状态s的折扣回报返回值为:
![]()
用图表示如下:
MC方法就是反复多次试验,求取每一个实验中每一个状态s的值函数,然后再根据GPI,进行策略改进、策略评估、策略改进....直到最优。
这中间就需要考虑一个情况,在一次试验中,对于某个状态s,可能只经历一次,也可能经历多次,也可能不经历,对于没有经历状态s的实验,在求取s的值函数时直接忽略该次实验就好。那么,对于其他两种情况时,怎么处理呢?
这里就有了两种方法:first-visit MC和every visit MC.
对于first-visit MC, 某一个状态s的值函数可以这样计算:
\[v(s) = \frac{{{G_{11}}(s) + {G_{21}}(s) + {G_{31}}(s) + \cdots }}{{N(s)}}\]
对于every-visit MC,某一个状态s的值函数可以这么计算:
\[v(s) = \frac{{{G_{11}}(s) + {G_{12}}(s) + \cdots + {G_{21}}(s) + {G_{22}}(s){\rm{ + }} \cdots + {G_{31}}(s){\rm{ + }}{G_{32}}(s) + \cdots }}{{N(s)}}\]
下面给出一次访问MC的伪代码如下所示:

2.起始点方法(Exploring Starts MC)
对于MC来说,经验也就是训练样本的完备性至关重要,因为完备的训练样本才能估计出准确的值函数。但是,正如前面所说的,很多情况下,我们无法保证在多次试验后,可以获得一个较为完备的分布,很可能大部分都是极为相似的试验,导致一部分状态根本无法遍历到,遇到这种情况我们该怎么办呢?很明显,我们需要再MC方法中保证每个状态都能被访问到才行啊。这时候,就有人提出了,我们不是有起始状态嘛,可以设置一个随机概率,使得所有可能的状态都有一定不为0的概率作为初始状态,这样不就能遍历到每一个状态了吗。这就是起始点方法的思想。
伪代码如下所示:

下面问题又来了,起始点方法中,似乎有个问题,初始状态是随机分配的,这样可以保证迭代过程中每一个状态行为对都能被选中,但这里面蕴含了一个假设:也就是假设所有动作都能被无限频繁地被选中。这个我的理解就是:在状态很多的情况下,如果要每一个状态作为起始状态被选中的话,按照随机不为0的概率,可能需要无限次之多,至少理论上是这样。但现实中,有时候很难成立,或者无法完全保证。那么,有没有其他方法,可以保证初始状态不变的同时,又能保证每个状态可以遍历到呢?
我们忽然想到了以前EE问题探索的时候,似乎ε-greedy就可以满足啊。对了,就是这个方法,伪代码如下:
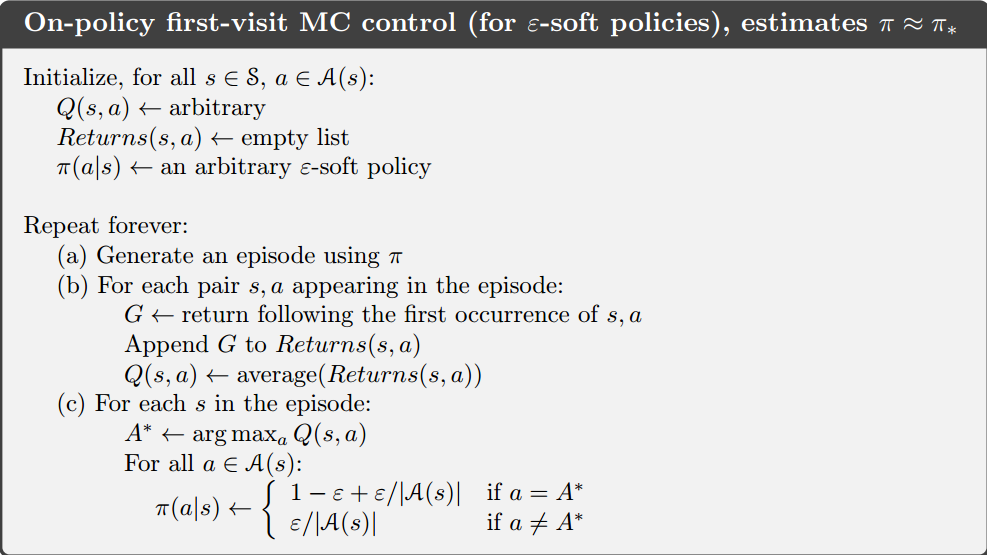
3. On-policy MC和Off-policy MC
下面得说一下同策略MC和离策略MC方法了。为什么会有这两种分类呢?可以想一下,MC算法不需要模型,只需要经验样本,只要足够多就可以近似估计出最优策略了,但这些训练样本怎么产生呢,如果训练样本根据另一套不是最优的策略生产的,那么在进行评估与改进的时候,就不太一样了。所以,这两种方法针对的就是数据产生的策略与评估改进的策略是否为统一策略进行分类的。
a.On-policy MC:同策略MC是指产生数据的策略与评估改进的策略是同一个策略。
b.Off-policy MC:离策略是指产生数据策略与评估改进的策略不是同一种策略。当然了,离策略MC也不是随便选择的,而是必须满足一定的条件。这个条件简单说就是:数据生成策略产生的状态要覆盖评估和改进策略的所有可能性。其实想想,这个还是比较苛刻的。
4.重要性采样(Importance Sampling)
同策略MC虽然更为简单方便,但实际应用中,离策略更为普遍。因此实际情况下,我们往往可以根据一些人为经验的策略给出一系列试验。
重要性采样是离策略方法使用时出现的问题。这一块内容读sutton原著的时候,其实我并没有理解的特别清楚,感觉写的比较拗口。于是参考了天津包子馅的知乎专栏,算是有点明白了。
重要性采样来源于求期望,比如说:求取下面的期望
![]()
如果其中的随机变量z的分布非常复杂时,我们无法根据解析的方法产生用于逼近期望的样本,这时候怎么办呢?我们可以选用一个概率分布非常简单,产生样本很容易的概率q(z),比如正态分布,这样,原本的期望如下:
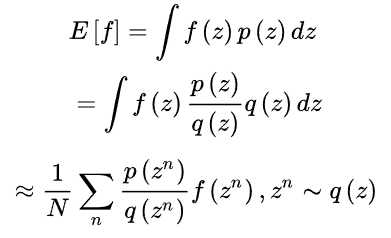
如果我们定义重要性权重:\[{\omega ^n} = \frac{{p({z^n})}}{{q\left( {{z^n}} \right)}}\],那么,普通的重要性采样求积分就如下图所示:
\[E\left[ f \right] = \frac{1}{N}\sum\limits_n {{\omega ^n}f\left( {{z^n}} \right)} \]
由上式可知,基于重要性采样的积分估计为无偏估计,即估计的期望值等于真实的期望。但是,基于重要性采样的积分估计的方差无穷大。这是因为,原来的被积分函数乘上一个重要性权重,这就改变了被积函数的形状和分布。尽管均值没有发生什么变化,但方差明显发生了改变。
当然了,在重要性采样中,使用的采样概率分布与原概率分布越接近,方差就越小。然而,被积分函数的概率往往很那求得,或者,没有简单的采样概率分布与之相似,这时候如果执迷不悟还使用分布差别很大的采样概率对原概率分布进行采样,方差就会趋近于无穷大。
其中一种减小重要性采样积分方差的方法就是采用加权重要性采样:\[E\left[ f \right] \approx \sum\limits_{n = 1}^N {\frac{{{\omega ^n}}}{{\sum\nolimits_{m = 1}^N {{\omega ^m}} }}} f({z^n})\]
好了,前面说完了重要性采样的基本概念,下面就说说这些与离策略方法有什么关系呢。这里是这么理解的,数据生成策略π所产生的轨迹概率分布相当于重要性采样中的q(z),用来评估和改进的策略μ对应的是那个复杂的p(z),因此利用数据生成策略所产生的累积函数返回值评估策略时,需要累积函数返回值前面乘以重要性权重。
那么,在评估改进的策略时,一次试验的概率是:
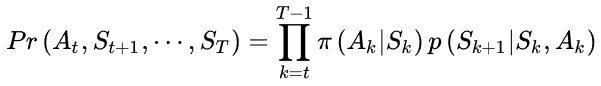
在数据生成策略下,相对应的实验概率为:
![]()
因此,重要性权重为:
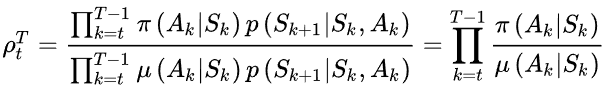
对于普通的重要性采样,值函数估计为:

下面用个简单的小例子来说明一下上面的式子:

加权的重要性采样值函数估计为:
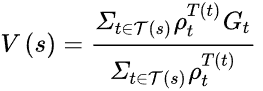
最后,给出离策略MC方法的一个伪代码:

最后,总结一下蒙特卡洛与动态规划的区别。
1.DP方法是基于模型的,而MC是无模型的。
2.DP是计算是自举的或引导性的(bootstrapping),而MC的计算是取样性的(sampling)。
MC的优缺点说明:
优点:a.蒙特卡洛方法可以从交互中直接学习优化的策略,而不需要一个环境的动态模型。这个样本很可能是大量的但容易获得的。
b.MC可以用于只知道样本的模型。
c.MC方法的每一个状态值计算都是独立计算的,不会影响其他的状态值。
缺点:a.需要大量重复的训练样本。
b.基于概率的,也就是不确定的。
参考文献
[1]. Reinforcement learning: an introduction.2017 Draft.
[2].https://zhuanlan.zhihu.com/p/25743759
[3].http://www.cnblogs.com/steven-yang/p/6507015.html
[4].http://www.cnblogs.com/jinxulin/p/3560737.html




