强化学习总结(2)--马尔科夫决策
RL问题的基础就是马尔科夫决策过程(MDP),因此,这一块内容虽然基础,但确是不得不总结的内容。网上虽然有很多博客、专栏介绍,但总感觉似是而非,有些还有些许错误。这里打算按照教材中的体系再度总结一下吧。这一块概念性的东西比较多,比如马尔科夫性质(无后效性),比如值函数、最优值函数、最优动作价值函数等等。下面会一一进行介绍。
1.几种马尔科夫模型的关系,引用一篇博客的图就是:

2.马尔科夫决策过程
一个马尔科夫决策过程由一个五元组构成M=(S,A,Ps,a,R,γ ),具体如下:
S:表示一组状态集合。
A:表示一组动作。
Ps,a表示状态转移概率。Ps,a表示当前状态下,经过动作a后,可能转移到其他各种状态的概率分布情况。比如,在状态s下执行动作a,转移到s'的概率可以表示为p(s'|s,a).
R:奖励函数。
γ是折扣率,又叫折扣因子。
回报(return):时刻t在某一状态下的表示:
\[\begin{array}{c}
{G_t} = {R_{t + 1}} + \gamma {R_{t + 2}} + {\gamma ^2}{R_{t + 3}} + \cdots \\
{\rm{ = }}{R_{t + 1}} + \gamma {G_{t + 1}}
\end{array}\](2.1)
其中γ是一个参数,属于[0,1],就是所谓的折扣率。
MDP的决策过程非常好理解,学过随机过程的应该都知道,就是:某个agent的初始状态为s0,然后根据策略选择一个动作a0执行,然后状态会按照Ps,a的转移概率转移到下一个状态s1,然后继续执行下一个动作a1,转移到s2,接下来继续执行....这个过程也比较好理解,不再赘述。
2.值函数
这个是MDP的核心,也是RL的核心概念。举个例子,下棋的时候,如果在第n步输了棋,那么只有状态sn和an,然后获得的一个立即奖励,但这个奖励怎么说明策略到底是好还是坏呢,这样就太草率了吧?因此,我们想到再定义一个函数,我们不用直接奖励作为最终的返回值,我们用一个历次奖励的累加组合,这样这个函数中就包括了前面每一步的信息,如果将这个作为每一步的返回值,那肯定比立即奖励函数好点吧,这就是值函数的由来。值函数可以表明当前状态下策略Π的长期奖赏。
值函数(就是状态值函数)定义为:\[{v_\pi }(s) = {{\rm E}_\pi }[{G_t}|{S_t} = s] = {{\rm E}_\pi}\left[ {\sum\limits_{k = 0}^\infty {{\gamma ^k}{R_{t + k + 1}}|{S_t} = s} } \right]\](2.2)
简单说就是,在策略π下状态s的值,这个值怎么来的呢,就是当前状态下回报return的期望。
然而,有了状态值函数还不够,如果考虑采取某个确定动作后得到的状态,这该怎么确定值呢,那就再定义一个值函数-----状态动作值函数。表示为:
\[{q_\pi }(s,a) = {{\rm E}_\pi }[{G_t}|{S_t} = s,{A_t} = a] = {{\rm E}_\pi }\left[ {\sum\limits_{k = 0}^\infty {{\gamma ^k}{R_{t + k + 1}}|{S_t} = s,{A_t} = a} } \right]\](2.3)
接下来,上述公式感觉没法用啊,能不能再继续展开一下呢,完全可以,bellman方程就是干这个事情的。于是就有了下式:
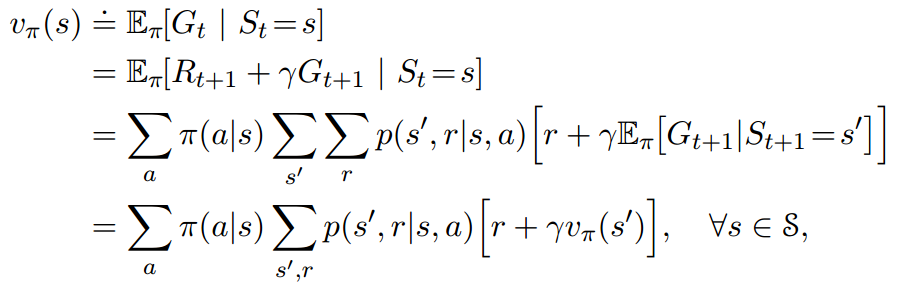 (2.4)
(2.4)
这个式子比较清晰,离散情况的,没什么具体可以说的,就是这个式子给出了值函数和下一个值函数的递推关系。
3.值函数的优化
有了值函数,接下来该怎么寻找最优策略呢,RL的工作就是寻找能使最终目标回报最大的策略。对于每一个状态,如果整个任务重复的回数足够多,那么每一个状态都会有许许多多的状态值函数,这中间,一定会有一个最大值,当然可能几个都是最大并列,这关系不大。定义最优值函数为\[{v_*}(s) = \mathop {\max }\limits_\pi {v_\pi }(s)\]
对应的最优动作状态值函数定义为:\[{q_*}(s,a) = \mathop {\max }\limits_\pi {q_\pi }(s,a)\](2.5)
然后,就该找到可以求解的公式了,如下所示:
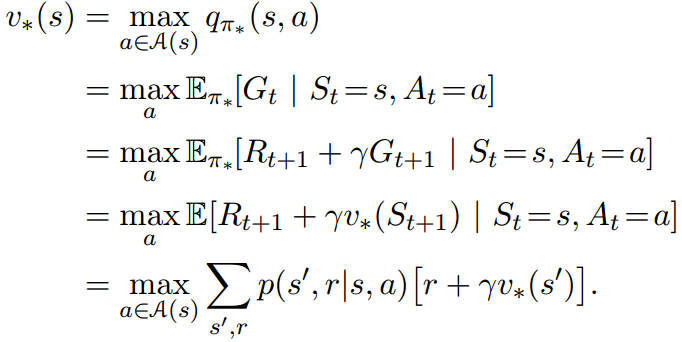
3.价值函数和动作价值函数的关系

策略迭代属于下一节的内容,就不放在这里讲了。
参考文献
[1]. Reinforcement learning: an introduction.2017 Draft.
[2].http://blog.csdn.net/greent2008/article/details/53995974
[3].http://blog.csdn.net/zz_1215/article/details/44138823





