强化学习总结（1）--EE问题

假设一个风投公司想使他的收益最大化,这时他总会面临一个两难问题: 何时去投资那些已经成功的公司？何时去投资那些还没有成功但具有很大潜力的公司？简单说就是，收益总是伴随着风险而存在. 这样的两难问题在日常生活中也是非常常见的，称为EE问题(Exploration and Exploitation tradeoff)。在数学领域，这个问题也早已被研究过，称为“多臂赌博机问题（Multi-armed bandit problem）”,又叫顺序资源分配问题（Sequential resource allocation problem）,都是指同一类问题，只是叫法不同。这个问题的各种解决方案广泛应用于广告推荐系统、源路由和棋类游戏中。

那么，为什么我们要学习这个内容呢，这个问题和我们要学习的RL有关系吗？

答：不只是有关系，关系还很大，后续的RL算法基本都要碰到EE问题，而解决方案基本都源自于本节，这个内容贯穿了整个RL的学习过程，并且借助这个问题，我们也可以大致了解RL的的关键--值函数是如何来的。因此，RL的开头要先讲这个内容。

问题描述：

现在你面前有十台赌博机，也就是十个动作选择，你每次只能选择一台赌博机操作一下，也就是你每次只能执行一个动作，然后赌博机会给你返回奖励，可多可少，也可以为0，每台赌博机的奖励都会遵从一个设定的概率分布，但你操作之初并不知道是什么分布，这是前提条件。然后，给你1000次甚至更多次数的操作机会（操作次数是已知的），你该如何保证自己获得的奖励最大？这就是多臂赌博机问题。

通用的描述就是：面对k个动作或选择，每次一个动作（选择），会获得一个服从某个固定概率分布的数值奖励。假设选择次数已知，那么如何最大化你的最终奖励？

基本思路：由于每一次的动作选择都会获得奖励，但具体在某次选择哪个动作必须要有一个依据，否则就变成随机选择了，既然如此，我们可否根据每一次动作的奖励来评估一下这个动作的好坏呢，这样的话，就可以直观地选择那些评价较高（即奖励较高）的动作了。那么，这个动作的评价值如何给出呢？在书中这样定义：

我们将在时间步长t采取的动作记为A_t，获得的奖励记为R_t， 采取某个动作a获得的动作评价值记为q_*（a），那么，\[{q_*} = {\rm E}[{R_t}|{A_t} = a]\] (1.1)

根据这个动作评价值，我们刚开始先经过少数有限次的遍历，然后接下来一直选择评价值高的动作不就行了，当然可以！！因为这样就已经可以一定程度上保证奖励比随机选择的要好了。但随之而来的又有一个疑问，那如果我们刚开始选出来的那个评价值较高的动作到后面奖励一直比较少，而真正评价高的动作我们刚开始并没有发现该怎么办？这种情况是存在的，尤其是当刚开始遍历次数较少，无法准确获得每一个选择背后的准确概率分布时，很容易犯这样的错误，即选择了刚开始评价值较高但实际上长期来看并不高的动作。那有人该问了，我们延长遍历的次数，争取获得一个较为可信的每个动作的概率分布，然后再选择不就可以了？当然没问题，实际上过去的研究人员也想到了这个方法，但遍历次数定为多少是合适的呢？毕竟我们的动作给定是有限的，万一总共是1000次选择，光为了获得每一个的概率分布就用掉了999次，那和随机选择也没什么区别啊，况且就算是999次也有可能无法得到概率分布该咋办。那么，我们就不能通过某种方法，在较少的次数内对动作的评价值进行一个较为可信的估计（即较为符合真实分布），然后用估计评价值代替真实值来作为下一次动作选择的参考呢，这样不就两全其美了呢？完全可以！！事实上，研究人员们就是这样做的，下面就来一一介绍这些动作评价值的估计方法。

1.动作-值方法(Action-Value Method)

    动作-值方法又叫做样本平均法(Sample-average method)，简单说每个动作评价值估计都是过去奖励的简单平均值。用公式表示如下：

\[{Q_t}(a) = \frac{{\sum\nolimits_{i = 1}^{t - 1} {{R_i} \cdot {1_{{A_i} = a}}} }}{{\sum\nolimits_{i = 1}^{t - 1} {{1_{{A_i} = a}}} }}\](1.2)

     这个估计方法思路非常简单，就是将该动作发生之前所有采取该动作获得奖励的和取平均值。当然，仅仅估计还不够，还得作出动作啊，怎么做出动作选择呢？当然是选估计值较大的了，于是就了贪心动作选择（greedy action method）的方法，就是依次估计动作的评价值，然后不断选择其中估计值最高的那一个。用公式就是：\[{Q_t}(A_t^*) = {\max _a}{Q_t}(a)\]，或者可以写作：\[A_t^* = \mathop {{\mathop{\rm argmax}\nolimits} }\limits_a {Q_t}(a)\](1.3)

       然后，我们就可以不断选择其中动作值高的动作了，这就是抽样平均中的贪心算法。但随之问题就来了，如果你利用贪心算法选择出的动作只是在刚开始动作值比较高，后面就不行了，或者说整体上不是较好的选择，但初期效果不错，那么很容易欺骗操作者，这就导致本应是最优选择的那个，因为刚开始动作值较低，无法被多次选择，这种问题是很常见的，那么这种情况该怎么办呢？也简单啊，我们就在每贪心算法选择之前，有0<ε<1的概率可以选择除当前最优选择之外的其他选择，这样，既利用了贪心算法考虑了当前的最优情况，又照顾到了长久情况下最优动作的选择，可以说两全其美了！！实际上，这就是ε-贪心算法，非常实用，后面的RL算法中很多都用了该算法来解决探索与利用的平衡问题。

       这里面还有一个编程上需要考虑的问题，那就是实现起来如何节省内存、提高运行速度。由上面可以知道，普通的样本平均方法可按照下式计算：\[{Q_n}{\rm{ = }}\frac{{{R_1}{\rm{ + }}R{}_2 + {R_3} +  \cdots  + {R_{n - 1}}}}{{n - 1}}\](1.4)

 但如果采用增量实现的话，所占内存和计算量都会减少，下面就是推导过程，看完就明白为何这么说了：

 

\[\begin{array}{c}
{Q_{n + 1}}{\rm{ = }}\frac{1}{n}\sum\limits_{i = 1}^n {{R_i}} = \frac{1}{n}\left( {{R_n} + \sum\limits_{i = 1}^{n - 1} {{R_i}} } \right) = \frac{1}{n}\left( {{R_n} + (n - 1)\frac{1}{{n - 1}}\sum\limits_{i = 1}^{n - 1} {{R_i}} } \right) = \frac{1}{n}\left( {{R_n} + (n - 1){Q_n}} \right)\\
= {Q_n} + \frac{1}{n}\left( {{R_n} - {Q_n}} \right)
\end{array}\]

 (1.5)

样本平均方法中的贪心算法和ε-贪心算法的伪代码（非常清晰明了，不用过多解释）：

 

 2.追踪不稳定问题

    样本平均方法，尤其是ε-贪心算法实用价值高，对于静态环境下的问题是非常好的选择。但是，凡是总有其他情况~~这里比如的情况是每个选择的奖励分布不是固定的，这就比较难办了，前面的方法也可以，但效果就不会那么好了。怎么办呢？有办法，将上面的1/（N(A)）改为α,这个α属于(0,1]，一个人为设定的常数。这样，就相当于为每一个奖励值提供了一个权重，这个权重呢，还满足离当前时刻越近，权重越大，离得越远，权重越小，这样，就算环境改变了，我们可以更多地参考当前的奖励，但也适当谨慎地参考长期的奖励，至少使得求出的动作值相对来说不太离谱~~当然，这只是基本方法，还有许多较为高级的、复杂的方法，但这已经不是本文的讨论范畴了。为什么一个α就可以有这么多优势，瞎扯的吧~~下面根据公式来看一下：

 

\[\begin{array}{c}
{Q_{n + 1}}{\rm{ = }}{Q_n}{\rm{ + }}\alpha {\rm{[}}{R_n} - {Q_n}{\rm{] = }}\alpha {R_n} + (1 - \alpha ){Q_n} = \alpha {R_n} + (1 - \alpha )[\alpha {R_{n - 1}} + (1 - \alpha ){Q_{n - 1}}]\\
= \alpha {R_n} + (1 - \alpha )\alpha {R_{n - 1}} + {(1 - \alpha )^2}{Q_{n - 1}}\\
= \alpha {R_n} + (1 - \alpha )\alpha {R_{n - 1}} + {(1 - \alpha )^2}\alpha {Q_{n - 2}} + \cdots + {(1 - \alpha )^{n - 1}}\alpha {R_1} + {(1 - \alpha )^n}{Q_1}\\
= {(1 - \alpha )^n}{Q_1} + \sum\limits_{i = 1}^n {\alpha {{(1 - \alpha )}^{n - i}}{R_i}}
\end{array}\]

(1.6)

  其中\[{(1 - \alpha )^n} + \sum\limits_{i = 1}^n {\alpha {{(1 - \alpha )}^{n - i}} = 1} \]，具体推导证明不在这里显示，根据归纳法很容易推出来。因此这两项可以称之为加权平均值。上面的式子基本已经可以说明前面说法的正确性了。

  这里已经很明显可以看出，α就是步长参数，这里需要说明的是，虽然α是一个常数，但每一步都要根据实际情况作出调整的。我们用α_n(a)表示经过n次动作选择后的步长参数。很显然，如果等于1/n，那就变成样本均值方法了，如果不等于的话，就得考虑是否会收敛的问题，借用别人ppt里的一张图说明问题：

 

 

      事实上，满足上述条件的步长参数序列通常收敛很慢或者需要较为有技巧性的调整，因此，理论用的多，实际里面基本很少用。

3.优化初始值的方法

     这种方法思路也很简单，前面方法的初始动作值都是设为0，然后一步步展开，那么，可否刚开始就设一个比较大的值如5呢？这样会不会效果好呢？首先，我们得考虑一下，为什么初始值的设定会影响动作值呢？动作值不是由以前奖励的平均值确定的吗，怎么和初始值又拉上关系了，并且就算有关系，那和其他奖励的影响程度是一样的吧~~当然，对于样本平均方法来说，是这样的！！但还得考虑式(1.6)的情况，并且从中可以看出，Q1似乎很重要啊，都单独列出来作为一项了啊~~因此，本种方法针对的是非静态问题下的选择问题，也就是上个小方法的问题。根据(1.6)可看出，初次选择的影响会一直影响后续的动作值，设为0可以减小偏差，因此是最常用的。但换个角度考虑，比如设初始值为+5，那么，刚开始，很少有选择的动作值会高于5，这样该选择会经常作为贪心选择，那么在探索的时候，就会探索的覆盖面更大一点，基本上在动作值收敛前，所有的动作都会被遍历到的。这样看来，这种方法的优势就是鼓励探索。下面用书上的一个对比图看一下设置初值带来的变化：

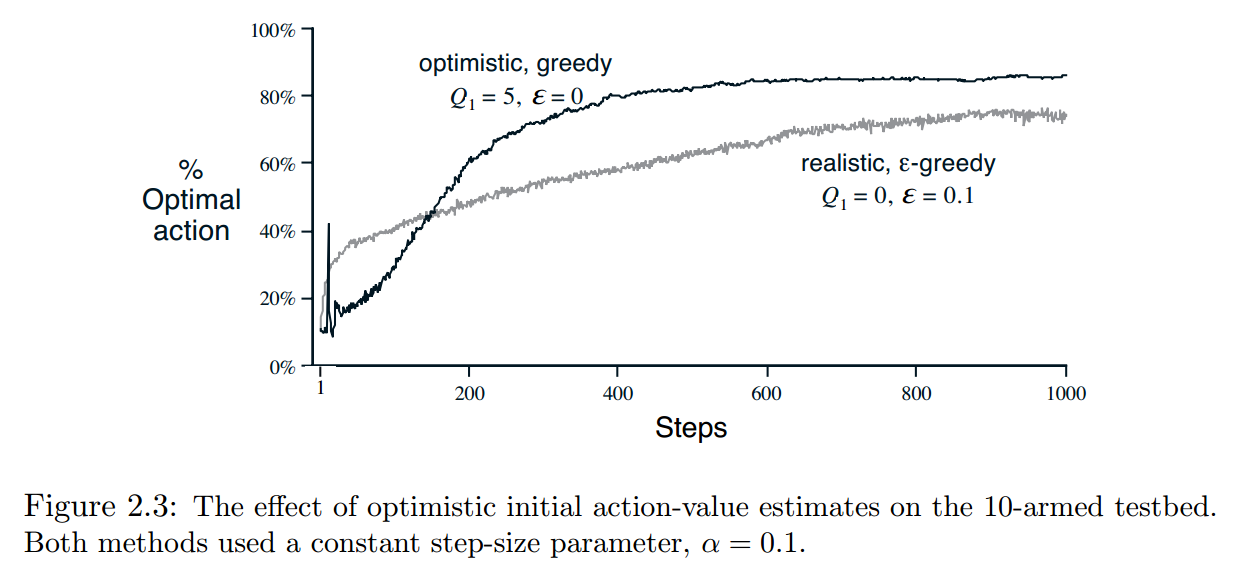
     从上图也能看出来，初值的设置的确会影响选取最优动作的概率。 这个图非常有意思，有兴趣可以深入分析一下，比如为何刚开始会有一个峰值呢？  

4.置信上界方法

    前面的方法，尤其是经典的ε-贪心算法，会有一定概率去做出探索，而不是局限于当前的局部最优选择。那么，探索的时候能不能不要随机选择一下，能不能让覆盖面大一点，尽量选那些以前没怎么选的动作，这样经过一段时间遍历，每一个动作的奖励分布都能差不多估计出来，那么最优动作被选的概率也会高一些啊~~~当然可以了！！事实上，这就是置信上界方法的核心思想。但问题来了，怎么构造这样的选择函数呢~~下面给出置信上界里的构造公式：

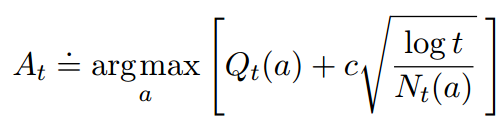（1.7）

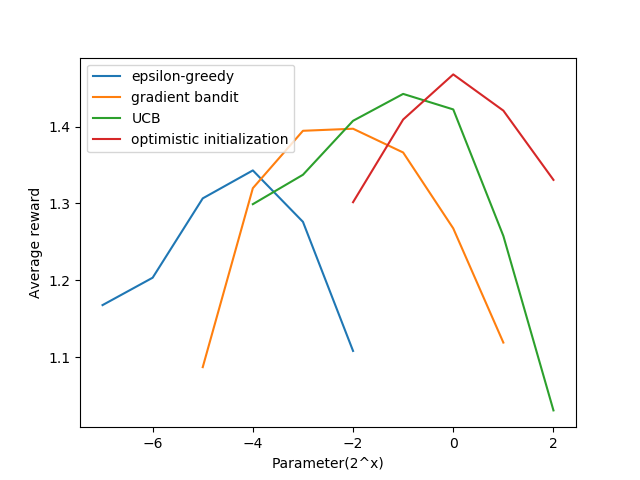
上面t是时间，N_t(a)是这段时间里动作a被选择的次数，c>0表示探索程度。这个方法理论上效果是非常好的，后面的图中会看到，只要参数调好，基本效果是最好的。但这个方法缺点非常明显：a.很难去解决不稳定问题，b.很难去解决大的状态空间问题

5.梯度方法

   这个方法思路更好理解，就是对每一个动作设置一个偏好，然后根据概率来选择动作，对应动作的偏好概率越大，这个动作被选择的次数就越多。偏好公式如下：

\[\Pr \{ {A_t} = a\}  = \frac{{{e^{{H_t}(a)}}}}{{\sum\nolimits_{b = 1}^k {{e^{{H_t}(b)}}} }} = {\pi _t}(a)\]

   更新偏好公式：

  

 

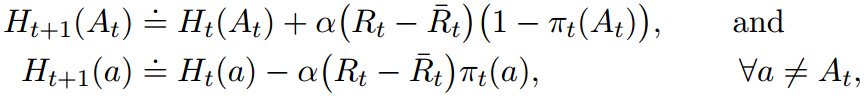
具体的公式推导比较长，但并不复杂，不在这里具体显示。

但必须说明，该方法属于梯度上升方法，经过推导证明可以得出：上述方法的期望梯度更新与期望奖励的梯度是一致的，并且上述梯度方法是随机梯度上升找那个的一个实例。上述方法并不需要奖励的baseline来选择动作。比如，我们将其设为0或者1000，这个算法仍然是随机梯度上升方法，baseline的选择不会影响算法的期望更新，但会影响方差和收敛率。因此，在实际找那个，选择奖励的平均值可能不是最好的，但在实际部署时是简单易行的，并且关键是work well！！

 

6.联系搜索

   到目前为止，我们只考虑了非联系性的任务，不需要把不同的行为和不同的情况联系起来。怎么理解呢，就是在这些任务中，当任务是静止时，就选取一个单一的最优动作就好了，当任务是非静态的时候，就跟踪最佳动作就好了。但是，在一般的强化学习任务中，有不止一种情况，我们需要的不仅仅是单一的解决方案，更多时候，我们需要的是一个策略，就是从状态到动作的一个映射。这似乎就和强化学习有点联系了~~~

    这个基本做了解就行，知道联系搜索介于多臂赌博机问题和完全强化学习之间。

    后面的方法已经超出教材范围了，但又是一些比较重要的、常用的方法，这里也稍作总结。

  7.软最大化方法（softmax method）

     经典的ε-贪心算法其实还有一个缺点，就是在探索时，选择动作是均匀的，那么能否通过新的方法改变动作选择呢规则呢？完全可以！！Softmax就是其中之一，规则为：

      

 

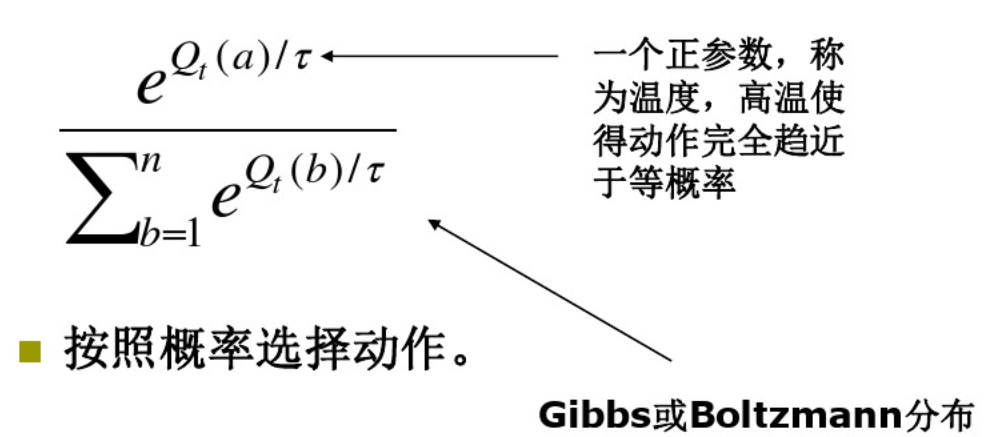
         这里还需要介绍一下强化比较的概念，后面会用到。选取一个参考标准做比较，这个标准就叫做参考奖赏。奖赏大于参考奖赏就强化。

        那么，我们首先根据Softmax方法决定动作选择的概率，即：

        

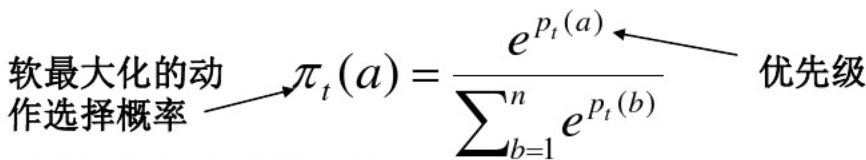
         更新优先级公式：

         \[{p_t}_{ + 1}(at) = {p_t}({a_t}) + \beta [{R_t} - \mathop {{R_t}}\limits^ -  ]\]

         参考奖赏更新公式：

          \[\mathop {{R_{t + 1}}}\limits^ -   = \mathop {{R_t}}\limits^ -   + \alpha [{R_t} - \mathop {{R_t}}\limits^ -  ]\]

   8.追踪方法

     强化比较只是维持整个奖赏过程的估计，通常不维持动作值估计。追踪方法可以同时维持动作值的估计和动作优先级（即动作选择概率）

     

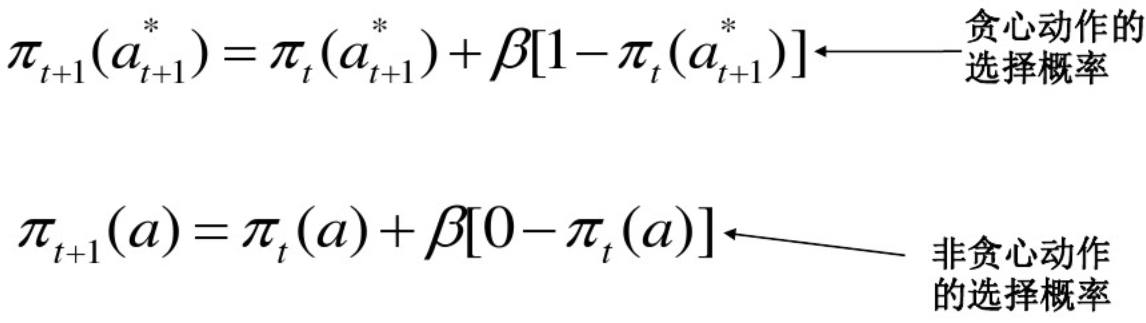
      动作值的更新不变，还是前面的\[{Q_{n + 1}} = {Q_n} + \alpha [{R_{n + 1}} - {Q_n}]\]

   9.Thompson Sampling

      这种方法思想也很简单，就是假定我们已知的初始动作值分布，然后每一步都更新这个分布（静态环境下）。通常情况下，更新计算都是非常复杂的，但都是对于一些特殊的分布来说会很容易，一个很好的选择就是在每一次选择时，都根据上一个最优动作的后验概率分布来确定下一个动作如何选，这就是Thompson Sampling。其实，在贝叶斯环境中，我们甚至可以计算出EE问题的最佳平衡，为什么这么说呢。。因为根据这个方法，我们可以对于任何的可能动作，都计算出一个可能立即奖赏的概率和由此产生的后验分布，如果给定足够多的次数的话，我们可以考虑所有的行动，以及每个行动下的所有可能奖励，然后计算挑出最好的就行了~~基本类似于暴力搜索方法~~但很遗憾，这种方法的计算量实在太大了，比如只有两个动作和两个奖赏，如果尝试1000次的话，这个搜索树将达到2²⁰⁰⁰个分支。尽管一般来说，不可能精确地执行这个庞大的计算，但也许可以近似~~~这种方法有效地将EE问题转化为完全强化学习问题的实例，尽管超出了本节的研究范畴，但仍可以用RL方法近似求解。

       上述方法都是一些基本且简单的方法，只是作为RL的入门基础，如果要专门学习推荐系统算法的话，上述内容就显得非常浅显了，还请查阅更多的资料进行详细学习。

       注：书中的代码github上很容易找到（https://github.com/ShangtongZhang/reinforcement-learning-an-introduction），主要是运行在python2.7下，代码测试过，主干部分基本没问题，但中间极个别地方可能需要自己调整，但问题都不大，调试一下基本都能跑出结果。这里非常感谢Shangtong Zhang的开源贡献！！

        本人代码运行环境为：VMware14 Pro+Ubuntu14.04.5+Anacnda2.7+Pycharm。

        本部分代码源自于上述github，部分修改，并增加了运行时间（实测有效）：

         

# coding=utf-8

from __future__ import print_function
import datetime
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import math

starttime = datetime.datetime.now()

class Bandit:
    # @kArm: # of arms
    # @epsilon: probability for exploration in epsilon-greedy algorithm
    # @initial: initial estimation for each action
    # @stepSize: constant step size for updating estimations
    # @sampleAverages: if True, use sample averages to update estimations instead of constant step size
    # @UCB: if not None, use UCB algorithm to select action
    # @gradient: if True, use gradient based bandit algorithm
    # @gradientBaseline: if True, use average reward as baseline for gradient based bandit algorithm
    def __init__(self, kArm=10, epsilon=0., initial=0., stepSize=0.1, sampleAverages=False, UCBParam=None,
                 gradient=False, gradientBaseline=False, trueReward=0.):
        self.k = kArm
        self.stepSize = stepSize
        self.sampleAverages = sampleAverages
        self.indices = np.arange(self.k)
        self.time = 0
        self.UCBParam = UCBParam
        self.gradient = gradient
        self.gradientBaseline = gradientBaseline
        self.averageReward = 0
        self.trueReward = trueReward

        # real reward for each action
        self.qTrue = []

        # estimation for each action
        self.qEst = np.zeros(self.k)

        # # of chosen times for each action
        self.actionCount = []

        self.epsilon = epsilon

        # initialize real rewards with N(0,1) distribution and estimations with desired initial value
        for i in range(0, self.k):
            self.qTrue.append(np.random.randn() + trueReward)
            self.qEst[i] = initial
            self.actionCount.append(0)

        self.bestAction = np.argmax(self.qTrue)

    # get an action for this bandit, explore or exploit?
    def getAction(self):
        # explore
        if self.epsilon > 0:
            if np.random.binomial(1, self.epsilon) == 1:
                np.random.shuffle(self.indices)
                return self.indices[0]

        # exploit
        if self.UCBParam is not None:
            UCBEst = self.qEst + \
                     self.UCBParam * np.sqrt(np.log(self.time + 1) / (np.asarray(self.actionCount) + 1))
            return np.argmax(UCBEst)
        if self.gradient:
            expEst = np.exp(self.qEst)
            self.actionProb = expEst / np.sum(expEst)
            return np.random.choice(self.indices, p=self.actionProb)
        return np.argmax(self.qEst)

    # take an action, update estimation for this action
    def takeAction(self, action):
        # generate the reward under N(real reward, 1)
        reward = np.random.randn() + self.qTrue[action]
        self.time += 1
        self.averageReward = (self.time - 1.0) / self.time * self.averageReward + reward / self.time
        self.actionCount[action] += 1

        if self.sampleAverages:
            # update estimation using sample averages
            self.qEst[action] += 1.0 / self.actionCount[action] * (reward - self.qEst[action])
        elif self.gradient:
            oneHot = np.zeros(self.k)
            oneHot[action] = 1
            if self.gradientBaseline:
                baseline = self.averageReward
            else:
                baseline = 0
            self.qEst = self.qEst + self.stepSize * (reward - baseline) * (oneHot - self.actionProb)
        else:
            # update estimation with constant step size
            self.qEst[action] += self.stepSize * (reward - self.qEst[action])
        return reward

figureIndex = 0

# for figure 2.1
def figure2_1():
    global figureIndex
    plt.figure(figureIndex)
    figureIndex += 1
    sns.violinplot(data=np.random.randn(200,10) + np.random.randn(10))
    plt.xlabel("Action")
    plt.ylabel("Reward distribution")

def banditSimulation(nBandits, time, bandits):
    bestActionCounts = [np.zeros(time, dtype='float') for _ in range(0, len(bandits))]
    averageRewards = [np.zeros(time, dtype='float') for _ in range(0, len(bandits))]
    for banditInd, bandit in enumerate(bandits):
        for i in range(0, nBandits):
            for t in range(0, time):
                action = bandit[i].getAction()
                reward = bandit[i].takeAction(action)
                averageRewards[banditInd][t] += reward
                if action == bandit[i].bestAction:
                    bestActionCounts[banditInd][t] += 1
        bestActionCounts[banditInd] /= nBandits
        averageRewards[banditInd] /= nBandits
    return bestActionCounts, averageRewards


# for figure 2.2
def epsilonGreedy(nBandits, time):
    epsilons = [0, 0.1, 0.01]
    bandits = []
    for epsInd, eps in enumerate(epsilons):
        bandits.append([Bandit(epsilon=eps, sampleAverages=True) for _ in range(0, nBandits)])
    bestActionCounts, averageRewards = banditSimulation(nBandits, time, bandits)
    global figureIndex
    plt.figure(figureIndex)
    figureIndex += 1
    for eps, counts in zip(epsilons, bestActionCounts):
        plt.plot(counts, label='epsilon = '+str(eps))
    plt.xlabel('Steps')
    plt.ylabel('% optimal action')
    plt.legend()
    plt.figure(figureIndex)
    figureIndex += 1
    for eps, rewards in zip(epsilons, averageRewards):
        plt.plot(rewards, label='epsilon = '+str(eps))
    plt.xlabel('Steps')
    plt.ylabel('average reward')
    plt.legend()


# for figure 2.3
def optimisticInitialValues(nBandits, time):
    bandits = [[], []]
    bandits[0] = [Bandit(epsilon=0, initial=5, stepSize=0.1) for _ in range(0, nBandits)]
    bandits[1] = [Bandit(epsilon=0.1, initial=0, stepSize=0.1) for _ in range(0, nBandits)]
    bestActionCounts, _ = banditSimulation(nBandits, time, bandits)
    global figureIndex
    plt.figure(figureIndex)
    figureIndex += 1
    plt.plot(bestActionCounts[0], label='epsilon = 0, q = 5')
    plt.plot(bestActionCounts[1], label='epsilon = 0.1, q = 0')
    plt.xlabel('Steps')
    plt.ylabel('% optimal action')
    plt.legend()


# for figure 2.4
def ucb(nBandits, time):
    bandits = [[], []]
    bandits[0] = [Bandit(epsilon=0, stepSize=0.1, UCBParam=2) for _ in range(0, nBandits)]
    bandits[1] = [Bandit(epsilon=0.1, stepSize=0.1) for _ in range(0, nBandits)]
    _, averageRewards = banditSimulation(nBandits, time, bandits)
    global figureIndex
    plt.figure(figureIndex)
    figureIndex += 1
    plt.plot(averageRewards[0], label='UCB c = 2')
    plt.plot(averageRewards[1], label='epsilon greedy epsilon = 0.1')
    plt.xlabel('Steps')
    plt.ylabel('Average reward')
    plt.legend()


# for figure 2.5
def gradientBandit(nBandits, time):
    bandits =[[], [], [], []]
    bandits[0] = [Bandit(gradient=True, stepSize=0.1, gradientBaseline=True, trueReward=4) for _ in range(0, nBandits)]
    bandits[1] = [Bandit(gradient=True, stepSize=0.1, gradientBaseline=False, trueReward=4) for _ in range(0, nBandits)]
    bandits[2] = [Bandit(gradient=True, stepSize=0.4, gradientBaseline=True, trueReward=4) for _ in range(0, nBandits)]
    bandits[3] = [Bandit(gradient=True, stepSize=0.4, gradientBaseline=False, trueReward=4) for _ in range(0, nBandits)]
    bestActionCounts, _ = banditSimulation(nBandits, time, bandits)
    labels = ['alpha = 0.1, with baseline',
              'alpha = 0.1, without baseline',
              'alpha = 0.4, with baseline',
              'alpha = 0.4, without baseline']
    global figureIndex
    plt.figure(figureIndex)
    figureIndex += 1
    for i in range(0, len(bandits)):
        plt.plot(bestActionCounts[i], label=labels[i])
    plt.xlabel('Steps')
    plt.ylabel('% Optimal action')
    plt.legend()

# Figure 2.6
def figure2_6(nBandits, time):
    labels = ['epsilon-greedy', 'gradient bandit',
              'UCB', 'optimistic initialization']
    generators = [lambda epsilon: Bandit(epsilon=epsilon, sampleAverages=True),
                  lambda alpha: Bandit(gradient=True, stepSize=alpha, gradientBaseline=True),
                  lambda coef: Bandit(epsilon=0, stepSize=0.1, UCBParam=coef),
                  lambda initial: Bandit(epsilon=0, initial=initial, stepSize=0.1)]
    parameters = [np.arange(-7, -1),
                  np.arange(-5, 2),
                  np.arange(-4, 3),
                  np.arange(-2, 3)]

    bandits = [[generator(math.pow(2, param)) for _ in range(0, nBandits)] for generator, parameter in zip(generators, parameters) for param in parameter]
    _, averageRewards = banditSimulation(nBandits, time, bandits)
    rewards = np.sum(averageRewards, axis=1)/time

    global figureIndex
    plt.figure(figureIndex)
    figureIndex += 1
    i = 0
    for label, parameter in zip(labels, parameters):
        l = len(parameter)
        plt.plot(parameter, rewards[i:i+l], label=label)
        i += l
    plt.xlabel('Parameter(2^x)')
    plt.ylabel('Average reward')
    plt.legend()


figure2_1()
epsilonGreedy(2000, 1000)
optimisticInitialValues(2000, 1000)
ucb(2000, 1000)
gradientBandit(2000, 1000)

# This will take somehow a long time
figure2_6(2000, 1000)

plt.show()

endtime = datetime.datetime.now()
print ("The total time: %s s" % (endtime-starttime))
# This will take somehow a long time：15min.

其中一个结果为：

 

参考文献：

[1]. Reinforcement learning: an introduction.2017 Draft.

[2].https://github.com/ShangtongZhang/reinforcement-learning-an-introduction

[3].https://wenku.baidu.com/view/adb2173766ec102de2bd960590c69ec3d5bbdba1.html