【逻辑】赛出25匹马的前3名

题       目

一共 25 匹马，每 5 匹马跑一次比赛，在不能使用计时器的情况下，最少要跑多少次能够决出这 25 匹马中的前 3 名？

 

解题思路

毋庸置疑，25 匹马一定是要先分五组，每组比一次，需要跑 5 次，这样能够决出各组内的第一名，一共产生 5 匹第一名的马，这 5 匹马分为一组，姑且成为冠军组。

那么这 25 匹马中的前 3 名一定就在冠军组中产生么？答案是否定的。

这 5 匹马只能证明是 5 组中各自的组内跑的最快的，但是不排除 某一组的第二名也很快，快过另一组的第一名。所以前 3 名并不能完全由 25 匹马决出的 5 匹冠军马中产生。

那么，如何公平的决出前三呢？

冠军组也跑一次吧，这是第 6 次。

冠军组的第一名绝对就是所有马中的第一名了，我们称这个马叫真正第一名。接下来我们需要决出真正的第二名的第三名。

真正的第二名的候选人有哪些呢？ 应该是冠军组的第二名，以及真正第一名原所在的组的第二名。

同理，真正的第三名候选人应该是冠军组的第三名，以及真正第一名原所在的组的第三名，还有冠军组第二名原所在的组的第二名。

有点绕，画个图给大家：

 

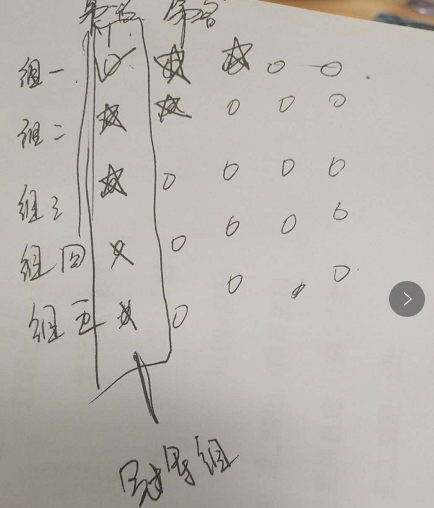
 五角星标注的马跑一次比赛，这是第7次。这样即可决出了第二名和第三名。

说了这么多，答案是 7 次哦~~