散列函数安全性的知识扩展
夏江华+2016012090+散列函数安全性的知识扩展
散列函数的具体应用
1、快速检索
它对于长字符串和短字符串都很有效,字符串中每个字符都有同样的作用,它巧妙地对字符的ASCII编码值进行计算,hash函数对于能够比较均匀地把字符串分布在散列表中。
1 int Hash(char *key){ 2 unsigned long h=0; 3 unsigned long x=0; 4 while(*key) 5 { 6 h=(h<<4)+(*key++); //h左移4位,当前字符ASCII存入h的低四位 7 if( (x=h & 0xF0000000L)!=0) 8 { //如果最高位不为0,则说明字符多余7个,如果不处理,再加第九个字符时,第一个字符会被移出 9 //因此要有如下处理 10 h^=(x>>24); 11 //清空28~31位 12 h&=~x; 13 } 14 } 15 return h % N; 16 }
2、数据校验
HASH函数有类似数据冗余校验类似的功能,但是它比简单的冗余校验碰撞的概率要小得多,顾而在现在密码学中总是用HASH来做关键数据的验证。
3、单向性的运用
利用HASH函数的这个特点,我们能够实现口令,密码等安全数据的安全存储。密码等很多关键数据我们需要在数据库中存储,但是在实际运用的过程中,只是作比较操作,顾而我们可以比较HASH结果。这一点在银行等系统中有所运用。
4、碰撞约束以及有限固定摘要长度
数字签名正是运用了这些特点来提高效率的。我们知道非对称加密算法速度较低,通过HASH处理我们可以使其仅仅作用于HASH摘要上,从而提高效率。
5、可以运用HASH到随机数的生成和密码,salt值等的衍生中
因为HASH算法能够最大限度的保证其唯一性,故而可以运用到关键数据的衍生中(从一个随机的种子数产生,并且不暴露种子本身秘密)。
散列函数安全性
在讲散列函数安全性之前,我先阐述一下生日攻击,再讲生日攻击之前,我先讲一下,概率论中我们学到的生日问题的期望——同月同日生的期望:
1 #include <iostream> 2 using namespace std; 3 int main() 4 { 5 double P(int n); 6 int n; 7 int i; 8 for(i = 1; i < 100; i += 3) 9 { 10 cout<<i<<"个人中至少有两个人生日相同的概率为:"<<1-P(i)<<endl; 11 } 12 return 0; 13 } 14 double P(int n) 15 { 16 double p = 1.0; 17 int i; 18 for(i = 1; i <= n; i++) 19 { 20 p *= (365-i+1)/365.0; 21 } 22 return p; 23 }
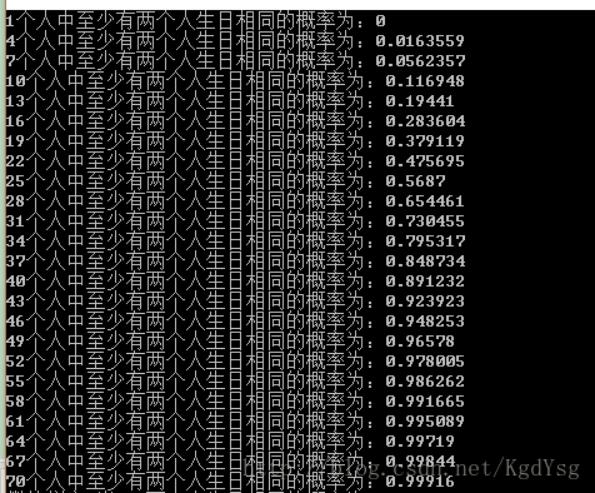
通过计算,随机抽取58人,其中有同日同月过生的人概率为99%,可见<<366。
这就是生日问题,那什么是生日攻击呢?
生日攻击就是写出好的hash function最大的绊脚石。如果你把散列函数的每个输入值想成是n个人中的一个,再把输出值想成是每个人的生日,那么生日问题就告诉我们,只需要很少的输入值,就会有很大的可能性有至少两个输出值完全相同,也就违反了散列函数的条件之一。攻击者也可以通过这一攻击方法,获取发送方的签名。
这就是生日攻击。
生日攻击严重影响了散列函数的安全性,目前比较有效的解决方法是:长消息摘要。
MD5:
MD5的根本原理:系统在并不知道用户密码的明码的情况下就可以确定用户登录系统的合法性。这不但可以避免用户的密码被具有系统管理员权限的用户知道,而且还在一定程度上增加了密码被破解的难度。
安全性:
通过碰撞的方法有可能构造两个具有相同MD5的信息,使MD5算法在目前的安全环境下有一点落伍。从实践角度,不同信息具有相同MD5的可能性还是非常低的,通常认为是不可能的,通过碰撞的方法也很难碰撞出复杂信息的MD5数值。
但是由于计算机能力不断的提升,目前可以依靠大型字典的方法,将常用密码进行MD5后建立数据库,然后和MD5数值进行对比,通过这样的方法来“破解”MD5。
SHA-1:
MD5 与SHA-1均是从MD4 发展而来,SHA-1与MD5 的最大区别在于其摘要比MD5 摘要长 32 比特,因而,SHA-1对强行攻击的强度更大。但是最终还是被Google攻破。
安全散列函数的发展:
1、生日攻击对Hash函数提出了一个必要的安全条件,即消息摘要必须足够长。40比特长的消息摘要,大概用2^20(大约100百万)次随机Hash可至少以1/2的概率找到一个碰撞。推荐160比特长的消息摘要。
2、在为文件签名之前,先向文件添加一个随机值,然后计算Hash值,再将文件、签名和随机值一起发送给接收者。这样,攻击者必须找出具有特定Hash值的伪造文件,这非常困难。
3、在为文件签名之前,对消息或文件做少许改动。这样,攻击者必须找出具有特定Hash值的伪造文件,这非常困难。
4、使用安全的Hash算法:安全的Hash算法生成的Hash值有足够多的位数。这样,攻击者在寻找两个具有相同Hash值的文件时就会非常困难。(和1类似)
md5算法来验证软件完整性时可能出现的问题
1、选择前缀碰撞
2004年的国际密码学会上,王小云等利用差分攻击算法首次实现MD5随机碰撞攻击,得到了MD5碰撞对。上述MD5随机碰撞攻击需要首次近似碰撞前的初始链接值得差分为0,因此又被称为相同前缀碰撞。2007年,Stevens提出了MD5选择前缀碰撞算法,展示了如何在一对任意选取的MD5消息前缀后,通过构造一对后缀使得两部分级联后的消息对发生碰撞的过程。
在总结MD5缺点之前,我们先对两个执行结果进行分析:
HelloWord.exe
GoodByeWorld.exe
通过对上方两个exe程序验证,md5 的确一样的。
(如何验证?这几位密码学家编写的“快速 MD5 碰撞生成器”:http://www.win.tue.nl/hashclash/fastcoll_v1.0.0.5.exe.zip 源代码:http://www.win.tue.nl/hashclash/fastcoll_v1.0.0.5_source.zip)
可见:这两个exe打印出不同的字符,但是它们的 MD5 都是一样的。(王小云所使用的攻击方法的改进版本)
2、缺点:
1、构造过程需要证书中的模数部分为8192比特,大大超出一般证书授权中心所要求的1048比特的标准上界。
2、选择前缀碰撞的部分组件无法多平台实现。
3、两个文件的执行结果不同,但MD5相同。
总结:MD5算法来验证软件完整性时可能出现的问题
1、不同软件或者执行文件的MD5可能是一样的。
2、对MD5的冲撞攻击是比较容易的,普通的计算机可以在几小时甚至几分钟之内找到冲撞对。
3、可以利用MD5的这个漏洞来伪造数字签名
4、2004、2005年王小云教授有关MD5发现,可以很快的找到MD5的“碰撞”,就是两个文件可以产生相同的“指纹”。(和2类似)
参考博客
https://blog.csdn.net/KgdYsg/article/details/54361218
https://www.zhihu.com/question/54307104
https://blog.csdn.net/shsalex/article/details/52329109
https://www.cnblogs.com/A2008A/archive/2012/08/10/2631840.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号