Elasticsearch 实现快速索引的原理
基本概念
Elasticsearch的文件存储,es是面向文档型数据库,一条数据在这里就是一个文档,用json作为序列化的格式,比如下面这条用户数据:
{
"name":"John",
"sex":"Male",
"age":25,
"birthDate":"1990/05/01",
"about":"I love to go rock climbing",
"interests":["sports","music"]
}
用Mysql这样的数据库存储就会容易想到建立一张User表,有各种字段,在es里这是一个文档,当然这个文档会属于一个User的类型,各种各样的类型存在于一个索引当中。es和关系型数据库对照:
关系型数据库:数据库 => 表 => 行 => 列
Elasticsearch:索引 => 类型 => 文档 => 字段
一个 Elasticsearch 集群可以包含多个索引(数据库),也就是说其中包含了很多类型(表)。这些类型中包含了很多的文档(行),然后每个文档中又包含了很多的字段(列)。
es的交互,可以使用Java API,也可以直接使用HTTP的Restful API方式。
索引
es索引的精髓:
一切设计都是为了提高搜索的性能,即为了提高搜索的性能,会牺牲某些其他方面,如插入/更新。如es在插入一条记录时,其实就是PUT一个json对象,这个对象中有多个fields,在插入这些数据到es的同时,es会为这些字段建立索引-倒排索引。
Elasticsearch是如何做到快速索引的呢?
什么是B-Tree索引?
二叉树查找效率是logN,同时插入新的节点不必移动全部节点,所以用树型结构存储索引,能同时兼顾插入和查询的性能。因此在这个基础上,再结合磁盘的读取特性(顺序读/随机读),传统关系型数据库采用了B-Tree/B+Tree这样的数据结构:

为了提高查询的效率,减少磁盘寻道次数,将多个值作为一个数组通过连续区间存放,一次寻道读取多个数据,同时也降低树的高度。
什么是倒排索引?

假设有一下几条数据:
ID Name Age Sex 1 Kate 24 Female 2 John 24 Male 3 Bill 29 Male
ID是Elasticsearch自建的文档id,那么Elasticsearch建立的索引如下:
Name: Term Posting List Kate 1 John 2 Bill 3 Age: Term Posting List 24 [1,2] 29 3 Sex: Term Posting List Female 1 Male [2,3]
Elasticsearch分别为每个field都建立了一个倒排索引,Kate, John, 24, Female这些叫term,而[1,2]就是Posting List。Posting list就是一个int的数组,存储了所有符合某个term的文档id。通过posting list这种索引方式似乎可以很快进行查找,比如要找age=24的同学。
Term Dictionary
Elasticsearch为了能快速找到某个term,将所有的term排个序,二分法查找term,logN的查找效率,就像通过字典查找一样,这就是Term Dictionary。现在再看起来,似乎和传统数据库通过B-Tree的方式类似啊,那么为什么说比B-Tree的查询快呢?
Term Index
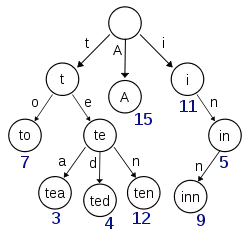
这棵树不会包含所有的term,它包含的是term的一些前缀。通过term index可以快速地定位到term dictionary的某个offset,然后从这个位置再往后顺序查找。
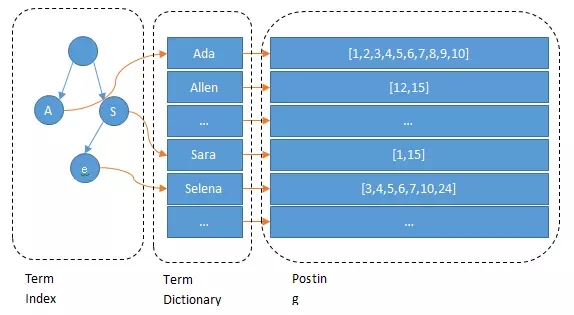
所以term index不需要存下所有的term,而仅仅是他们的一些前缀与Term Dictionary的block之间的映射关系,再结合FST(Finite State Transducers)的压缩技术,可以使term index缓存到内存中。从term index查到对应的term dictionary的block位置之后,再去磁盘上找term,大大减少了磁盘随机读的次数。
假设我们现在要将mop, moth, pop, star, stop and top(term index里的term前缀)映射到序号:0,1,2,3,4,5(term dictionary的block位置)。最简单的做法就是定义个Map,大家找到自己的位置对应入座就好了,但从内存占用少的角度想想,有没有更优的办法呢?答案就是:FST。
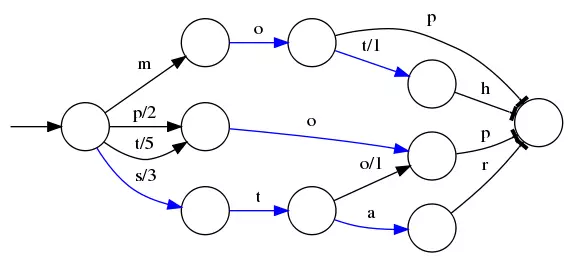
⭕️ 表示一种状态
–> 表示状态的变化过程,上面的字母/数字表示状态变化和权重
将单词分成单个字母通过⭕️和–>表示出来,0权重不显示。如果⭕️后面出现分支,就标记权重,最后整条路径上的权重加起来就是这个单词对应的序号。
FST以字节的方式存储所有的term,这种压缩方式可以有效的缩减存储空间,使得term index足以放进内存,但这种方式也会导致查找时需要更多的CPU资源。
压缩技巧
Elasticsearch里除了上面说到用FST压缩term index外,对posting list也有压缩技巧。如果Elasticsearch需要对同学的性别进行索引会怎样?如果有上千万个同学,而世界上只有男/女这样两个性别,每个posting list都会有至少百万个文档id。Elasticsearch是如何有效的对这些文档id压缩的呢?
增量编码压缩,将大数变小数,按字节存储
首先,Elasticsearch要求posting list是有序的(为了提高搜索的性能,再任性的要求也得满足),这样做的一个好处是方便压缩,看下面这个图例:
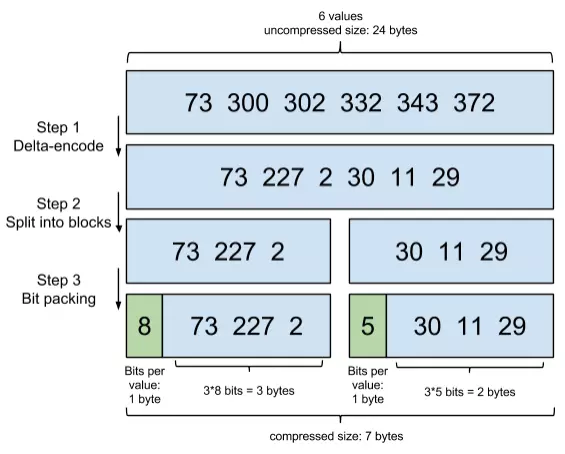
原理就是通过增量,将原来的大数变成小数仅存储增量值,再精打细算按bit排好队,最后通过字节存储,而不是大大咧咧的尽管是2也是用int(4个字节)来存储。
Roaring bitmaps
说到Roaring bitmaps,就必须先从bitmap说起。Bitmap是一种数据结构,假设有某个posting list:[1,3,4,7,10],那么对应的bitmap就是:[1,0,1,1,0,0,1,0,0,1]。
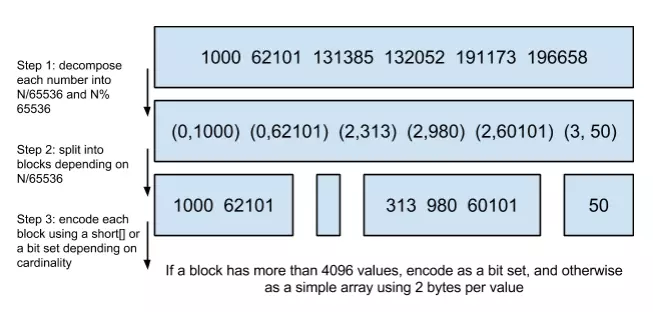
”为什么是以65535为界限?”
程序员的世界里除了1024外,65535也是一个经典值,因为它=2^16-1,正好是用2个字节能表示的最大数,一个short的存储单位,注意到上图里的最后一行“If a block has more than 4096 values, encode as a bit set, and otherwise as a simple array using 2 bytes per value”,如果是大块,用节省点用bitset存,小块就豪爽点,2个字节我也不计较了,用一个short[]存着方便。
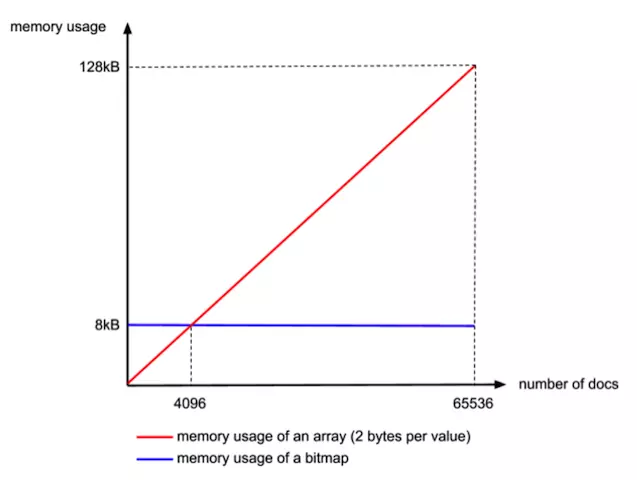
那为什么用4096来区分采用数组还是bitmap的阀值呢?
这个是从内存大小考虑的,当block块里元素超过4096后,用bitmap更剩空间: 采用bitmap需要的空间是恒定的: 65536/8 = 8192bytes 而如果采用short[],所需的空间是: 2*N(N为数组元素个数) 小明手指一掐N=4096刚好是边界:
联合索引
上面说了半天都是单field索引,如果多个field索引的联合查询,倒排索引如何满足快速查询的要求呢?
利用跳表(Skip list)的数据结构快速做“与”运算,或者利用上面提到的bitset按位“与”。先看看跳表的数据结构:

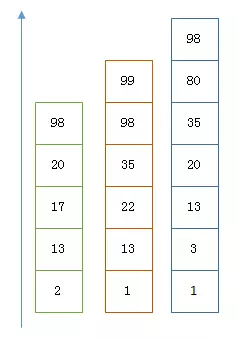
如果使用跳表,对最短的posting list中的每个id,逐个在另外两个posting list中查找看是否存在,最后得到交集的结果。如果使用bitset,就很直观了,直接按位与,得到的结果就是最后的交集。


