CF1988E

CF1988E

题意

多组数据，每组数据给定长度为 \(n(1 \leqslant n \leqslant 5 \times 10^5)\) 的排列 \(a\)。定义 \(f(a)\) 表示所有子段中最小元素的和，及 \(f(a)=\sum_{l=1}^n\sum_{r=l}^n \min_{l\le i\le r}a_i\) 对于每个 \(i\)，解决以下问题：从 \(a\) 删除 \(a_i\), 得到 \(b = [a_1,a_2,\ldots,a_{i-1},a_{i+1},\ldots,a_{n}]\)，计算 \(f(b)\)。

思路

• 首先我们可以通过单调栈求出 \(ls_i, rs_i\) 表示 \(i\) 左边和右边第一个比 \(a_i\) 小的元素，然后就可以求出 \(f(a) = \sum\limits_{i -= 1}^n a_i(i - ls_i)(rs_i - i)\)。

• 接下来枚举 \(i\) 考虑删除 \(i\) 后对答案的影响：

  • 对于左端点或右端点是 \(i\) 的子段，要减去它们的答案。
  • 对于 \(ls_i < 左端点 < i, i < 右端点 < rs_i\) 的子段，它们本来的最小元素为 \(a_i\)，但是 \(i\) 被删掉了，它们的答案是多少？

• 第一种情况：令 \(s1_i, s2_i\) 分别表示以 \(i\) 为右端点和以 \(i\) 为左端点的子段中最小元素的和。 那么有 \(\begin{cases} s1_i = s1_{ls_i} + a_i(i - ls_i) \\ s2_i = s2_{rs_i} + a_i(rs_i - i) \end{cases}\) ，注意 \([i, i]\) 这个区间被算了两次。证明一下：以 \(s1_i\) 为例，当左端点 \(\leqslant ls_i\) 时，区间答案和就是 \(s1_{ls_i}\)，否则子段的最小元素为 \(a_i\)，总和为 \(s1_{ls_i} + a_i(i - ls_i)\)。\(s2_i\) 同理。

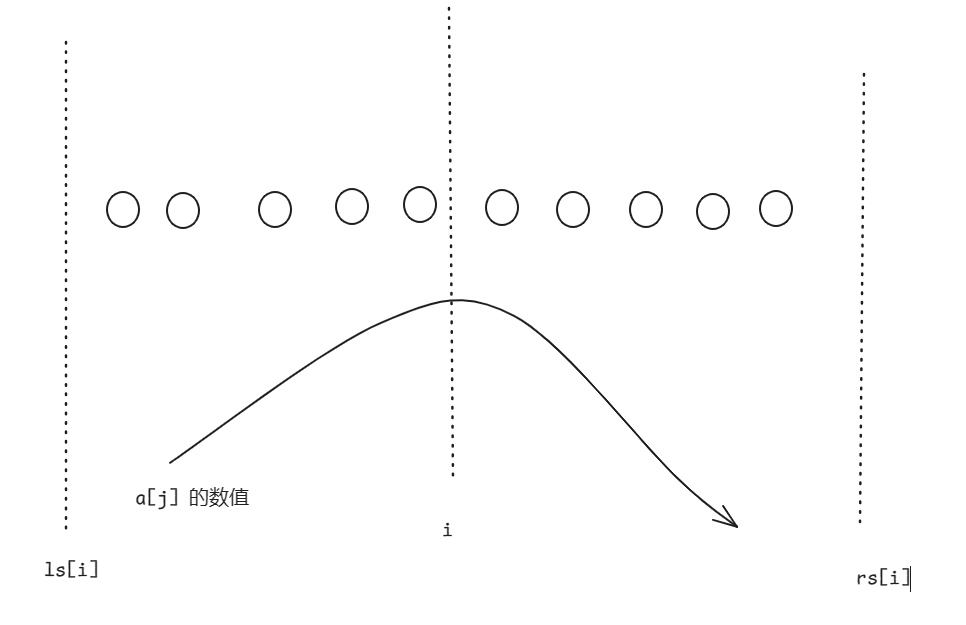
• 第二种情况：我们可以发现只有 \(rs_j = i\) 或 \(ls_j = i\) 的 \(a_j\) 才可能成为新的最小值。并且这些 \(j\) 的数值满足下图的关系，如果不满足它们的 \(ls_i / rs_i\) 就不可能是 \(i\)。然后我们就可以尝试暴力枚举 \(j\)，看一下左端点 \(l\) 和右端点 \(r\) 要满足什么要求才能使删除 \(a_i\) 后 \(a_j\) 是子段最小值。为了方便，令 \(p_{i, x}\) 为满足 \(rs_j = i\) 的所有 \(j\) 中从大到小第 \(x\) 个，\(q_{i, y}\) 为满足 \(ls_j = i\) 的所有 \(j\) 中从小到大第 \(y\) 个。

  • 对于 \(p_{i, x}\) 有 \(\begin{cases} p_{i, x + 1} < l \leqslant p_{i, x}, x < \lvert p_i\rvert \\ ls_i < l \leqslant p_{i, x}, x = \lvert p_i \rvert \end{cases}\) 。设 \(y'\) 为最小的 \(y\) 使得 \(a_{q_{i, y'}} < a_{p_{i, x}}\)，则 \(i < r < q_{i, y'}\)。若不存在 \(y'\)，则 \(i < r < rs_i\)
  • 对于 \(q_{i, y}\) 有 \(\begin{cases} q_{i, y} < r \leqslant q_{i, y + 1}, y < \lvert q_i\rvert \\ ls_i < r \leqslant q_{i, y}, y = \lvert q_i \rvert \end{cases}\)。设 \(x'\) 为最小的 \(x\) 使得 \(a_{p_{i, x'}} > a_{q_{i, y}}\)，则 \(p_{i, x'} < r < i\)。若不存在 \(y'\)，则 \(ls_i< r < i\)
  • 因为 \(p_i, q_i\) 内部都是有序的，所以做有序序列合并即可。还需要注意一下边界问题。

• 但是暴力枚举的时间复杂度是正确的吗？答案为是的！因为每个点都只有一个 \(ls_i, rs_i\)。所以暴力枚举的时间复杂度是 \(O(2n)\)。再加上单调栈求 \(ls_i, rs_i\) ，总时间复杂度是 \(O(n)\) 的

  

#include <iostream>
#include <vector>

using namespace std;
using ll = long long;

const int MAXN = 5e5 + 5;

ll sum, s1[MAXN], s2[MAXN];
vector<int> p[MAXN], q[MAXN];
int T, n, top, stk[MAXN], cnt[MAXN], a[MAXN], ls[MAXN], rs[MAXN];

ll work(int x) { 
  ll ret = 0;
  int n = p[x].size(), m = q[x].size();
  //cout << n << ' ' <<m << ' ';
  for (int i = 0, j = 0; i < n || j < m; ) { // 有序列合并
    if (i < n && (j == m || a[p[x][i]] > a[q[x][j]])) {
      ret += 1ll * (p[x][i] - (i + 1 < n ? p[x][i + 1] : ls[x])) * (j < m ? q[x][j] - x - 1 : rs[x] - x - 1) * a[p[x][i]], i++;
    } else {
      ret += 1ll * (i < n ? x - p[x][i] - 1 : x - ls[x] - 1) * ((j + 1 < m ? q[x][j + 1] : rs[x]) - q[x][j]) * a[q[x][j]], j++;
    }
  }
  return ret;
}

void Solve() {
  cin >> n, s2[n + 1] = 0;
  for (int i = 1; i <= n; i++) { // 单调栈
    cin >> a[i], ls[i] = 0, rs[i] = n + 1;
    while (top && a[stk[top]] > a[i]) {
      rs[stk[top--]] = i;
    }
    ls[i] = stk[top], stk[++top] = i;
  }
  for (int i = 1; i <= n; i++) {
    q[ls[i]].push_back(i);
    s1[i] = s1[ls[i]] + 1ll * (i - ls[i]) * a[i];
    sum += 1ll * (rs[i] - i) * (i - ls[i]) * a[i];
    //cout << ls[i] << ' ' << rs[i] << '\n';
  }
  for (int i = n; i; i--) {
    p[rs[i]].push_back(i);
    s2[i] = s2[rs[i]] + 1ll * (rs[i] - i) * a[i];
  }
  //cout << sum << ' ';
  for (int i = 1; i <= n; i++) { // 枚举删除的点
    cout << sum - s1[i] - s2[i] + a[i] - 1ll * (i - ls[i] - 1) * (rs[i] - i - 1) * a[i] + work(i) << " ";
    p[i].clear(), q[i].clear();
  }
  p[n + 1].clear(), q[0].clear();
  cout << '\n';
}

int main() {
  ios::sync_with_stdio(0), cin.tie(0);
  for (cin >> T; T--; sum = top = 0) {
    Solve();
  }
  return 0;
}