Hamilton cycle
1.1 Hamilton cycle
HAMILTON-CYCLE. Given an undirected graph G = (V, E), does there exist a
cycle Γ that visits every node exactly once?
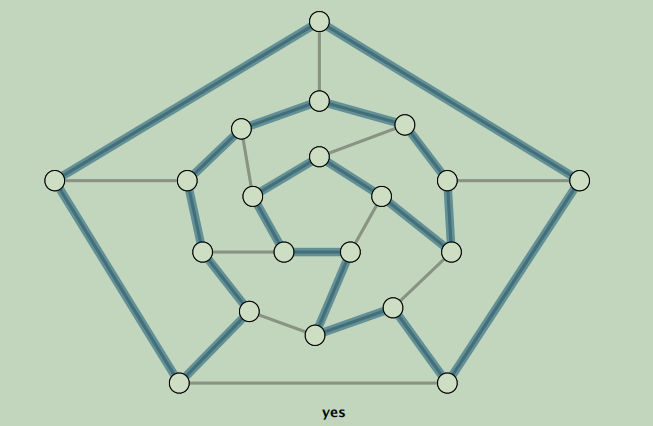
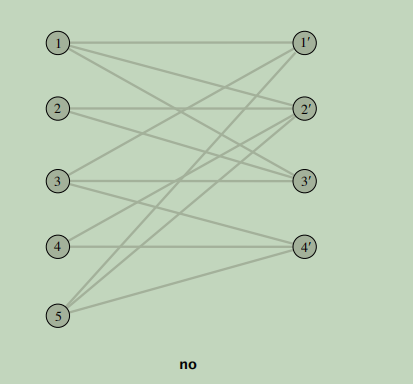
一个有解的图,一个没有解的图如下:
2.1 Directed Hamilton cycle reduces to Hamilton cycle
DIRECTED-HAMILTON-CYCLE. Given a directed graph G = (V, E), does there exist
a directed cycle Γ that visits every node exactly once?
关于有向哈密尔顿圈问题可以规约到哈密尔顿问题证明如下(DIRECTED-HAMILTON-CYCLE ≤ P HAMILTON-CYCLE.):
Pf. Given a directed graph G = (V, E), construct a graph Gʹ with 3n nodes.
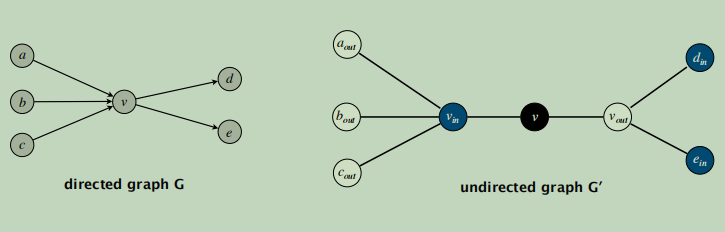
Lemma. G has a directed Hamilton cycle iff Gʹ has a Hamilton cycle.
2.1.1 证明
Pf. ⇒
- Suppose G has a directed Hamilton cycle Γ.
- Then Gʹ has an undirected Hamilton cycle (same order).
Pf. ⇐
- Suppose Gʹ has an undirected Hamilton cycle Γʹ.
- Γʹ must visit nodes in Gʹ using one of following two orders:
…, black, white, blue, black, white, blue, black, white, blue, …
…, black, blue, white, black, blue, white, black, blue, white, … - Black nodes in Γʹ comprise either a directed Hamilton cycle Γ in G,
or reverse of one.
3.1 3-satisfiability reduces to directed Hamilton cycle
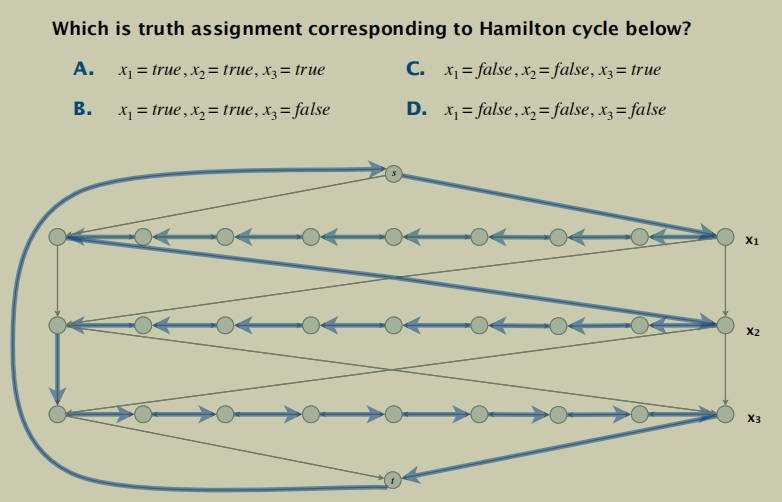
Construction. Given 3-SAT instance Φ with n variables xi and k clauses.
- Construct G to have 2^n Hamilton cycles.
- Intuition: traverse path i from left to right ⇔ set variable xi = true.

一个3元可满足性问题包含n个变量以及k个子模块,我们构造出一个2^n结点个数的图G。存在任意一个从左到右的路径<->xi=true. 右到左<->xi=false.
A problem:
3.1.1 3-satisfiability reduces to directed Hamilton cycle
Construction. Given 3-SAT instance Φ with n variables xi and k clauses.
- For each clause: add a node and 2 edges per literal.
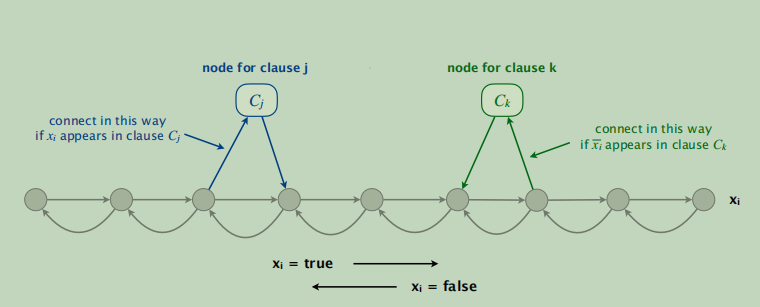
首先我们的构造方法是这样的:给你一个文法式n个变量k个子模块。对于每一个子模块添加一个结点两条边。
可以看到图中的子模块Cj和Ck分别表示的是: 如果xi是从右到左流入Ck的那么Ck中表示的则是xi“非”同理可得Cj中为xi。
一个完整的实例图如下:
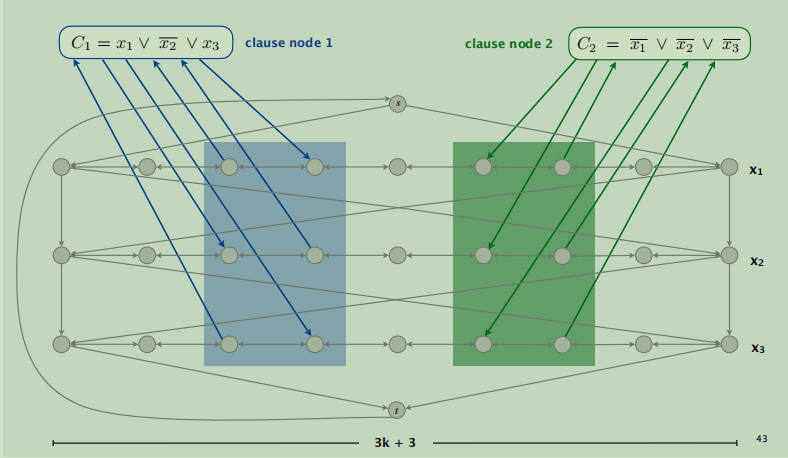
3.1.2 烦人的证明又来了!
Lemma. Φ is satisfiable iff G has a Hamilton cycle
Pf. ⇒
- Suppose 3-SAT instance Φ has satisfying assignment x*.
- Then, define Hamilton cycle Γ in G as follows:
- if x*i= true, traverse row i from left to right
- if x*i= false, traverse row i from right to left
- for each clause Cj , there will be at least one row i in which we are
going in “correct” direction to splice clause node Cj into cycle
(and we splice in Cj exactly once)
这种充分性其实不可靠的因为我可以将X1,x2,x3全部设置为true,那么显然哈密尔顿圈不满足。。。X1就重复了两次。
Pf. ⇐
- Suppose G has a Hamilton cycle Γ.
- If Γ enters clause node Cj , it must depart on mate edge.
- nodes immediately before and after Cj are connected by an edge e ∈ E
- removing Cj from cycle, and replacing it with edge e yields Hamilton
cycle on G –
- Continuing in this way, we are left with a Hamilton cycle Γʹ in
G – { C1 , C2 , …, Ck }. - Set x*i= true if Γʹ traverses row i left-to-right; otherwise,
- set x*i= false. traversed in “correct” direction, and each clause is satisfied.
4.1 3-satisfiability reduces to longest path
Pf 1. Redo proof for DIR-HAM-CYCLE, ignoring back-edge from t to s.
Pf 2. Show HAM-CYCLE ≤ P LONGEST-PATH
5.1 TSP
TSP. Given a set of n cities and a pairwise distance function d(u, v),
is there a tour of length ≤ D ?
5.1.1 HAM-CYCLE ≤ P TSP



