回溯算法小细节

目录

看下面这个题：

无重复字符串的排列组合。编写一种方法，计算某字符串的所有排列组合，字符串每个字符均不相同。
示例1:
输入：S = "qwe"
输出：["qwe", "qew", "wqe", "weq", "ewq", "eqw"]
示例2:
输入：S = "ab"
输出：["ab", "ba"]

该题一般有两种常见解法一种是交换全排列而另一种就是回溯算法。
具体怎么实现就不说了，主要讲讲如果用回溯算法怎么减少空间复杂度！

解法一：

public String[] permutation(String S) {
List<String> list=new ArrayList<>();
char[] temp=S.toCharArray();
int length=S.length();
boolean[] flag=new boolean[length];
backtrack(temp,list,length,"",flag);
String [] res= new String[list.size()];
      if(length==0) return  res;
for(int i=0;i<list.size();i++){
  res[i]=list.get(i);
}

      return  res;
  }

  public  void backtrack(char[] temp,List<String> list,int length,String str,boolean[] flag){
      if(str.length()==length){
          list.add(str);
          return;
      }
      for(int i=0;i<temp.length;i++) {
          if(flag[i]) continue;
          flag[i]=true;
          backtrack(temp, list, length, str + temp[i], flag);
          flag[i]=false;
      }

  }

解法二：

 public String[] permutation(String S) {
        char[] arrS = S.toCharArray();
        boolean[] used = new boolean[S.length()];
        LinkedList<String> result = new LinkedList<>();
        dfs(arrS, used, new StringBuilder(), result);
        return result.toArray(new String[0]);
    }

    private void dfs(char[] data, boolean[] used, StringBuilder stringBuilder, LinkedList<String> result) {
        if (stringBuilder.length() == data.length) {
            result.add(stringBuilder.toString());
            return;
        }
        for (int i = 0; i < data.length; i++) {
            if (used[i] == true) {
                continue;
            }
            stringBuilder.append(data[i]);
            used[i] = true;
            dfs(data, used, stringBuilder, result);
            stringBuilder.deleteCharAt(stringBuilder.length() - 1);
            used[i] = false;
        }
    }

简单说一下两种算法的思想吧：都用运用回溯算法，我们都知道回溯用的是栈递归。
第一种方法是利用栈递归的过程中进行状态重置，因为第一种方法用的是临时变量默认存在在java栈区，那么随着方法的递归返回，该变量的值也就实现了重置

而第二种方法直接在堆中开辟了一块StringBuilder。这种堆区中的变量不会随着递归栈的弹出而发生变化，不像临时变量会随着方法的结束而死亡。那这种方法就必须手动在一次递归结束后进行状态重置。 stringBuilder.deleteCharAt(stringBuilder.length() - 1);

总结：两种方法各有好坏以下是运行结果图：

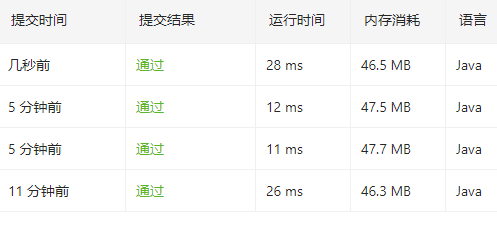
可以看到方法一没有开辟额外的空间因此内存消耗为46M左右比方法二开辟堆空间要少一点，不过在时间却慢于方法二，典型的拿时间换空间。

解法一因在递归回退和前进过程中要存入操作数和被操作数，因此在时间上要稍逊于解法二。