Java蓝桥杯
1、特殊回文数:123321是一个非常特殊的数,它从左边读和从右边读是一样的。输入一个正整数n, 编程求所有这样的五位和六位十进制数,满足各位数字之和等于n 。

public class Main { public static void main(String args[]) { Scanner sc = new Scanner(System.in); int num = sc.nextInt(); sc.close(); for(int i=10000;i<100000;i++) { if(isHuiWen(i)) { if(len(i)==5) { if((i/10000*2 + i/1000%10*2 + i/100%100) == num) { System.out.println(i); } } if(len(i)==6) { if((i/10000*2 + i/1000%10*2 + i/100%100*2) == num) { System.out.println(i); } } } } } public static boolean isHuiWen(int n) { String str = String.valueOf(n); int i=0,j=str.length()-1; while(i<j) { if(str.charAt(i++)!=str.charAt(j--)) { return false; } } return true; } public static int len(int n) { String str = String.valueOf(n); return str.length(); } }
2、杨辉三角形又称Pascal三角形,它的第i+1行是(a+b)i的展开式的系数。它的一个重要性质是:三角形中的每个数字等于它两肩上的数字相加。下面给出了杨辉三角形的前4行:
1
1 1
1 2 1
1 3 3 1
给出n,输出它的前n行。
数据规模和约定:1<=n<=34

import java.util.*; public class Main { public static void main(String args[]) { int n,i,j; int arr[][] = new int[34][34]; Scanner sc = new Scanner(System.in); n = sc.nextInt(); sc.close(); for(i=0;i<n;i++) { for(j=0;j<n;j++) { //第一列填值 arr[i][0] = 1; //对角线填值 if(i==j) { arr[i][j]=1; } } } // 求和,每个元素的值等于这个元素上一行上一列的值加上上一行本列元素的值 for(i=2;i<n;i++) { for(j=1;j<n;j++) { arr[i][j]=arr[i-1][j-1]+arr[i-1][j]; } } for(i=0;i<n;i++) { for(j=0;j<n;j++) { if(arr[i][j]!=0) { System.out.print(arr[i][j]+" "); } } System.out.println(); } } }
3、给出一个包含 n个整数的数列,问整数a在数列中的第一次出现是第几个。

public class Main { public static void main(String args[]) { Scanner sc = new Scanner(System.in); int index = 0; int n = sc.nextInt(); int arr[] = new int[n]; sc.nextLine(); String string = sc.nextLine(); int findnum = sc.nextInt(); sc.close(); String[] line = string.split(" "); for(int i=0;i<n;i++) { arr[i] = Integer.parseInt(line[i]); } for(int i=0;i<n;i++) { if(arr[i] == findnum) { index = i+1; } } if(index>0) System.out.println(index); else System.out.println(-1); } }
4、问题描述: 利用字母可以组成一些美丽的图形,下面给出了一个例子:
ABCDEFG
BABCDEF
CBABCDE
DCBABCD
EDCBABC
这是一个5行7列的图形,请找出这个图形的规律,并输出一个n行m列的图形。

public class Main { public static void main(String args[]) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int m = sc.nextInt(); for(int i=0;i<n;i++) { for(int j=0;j<m;j++) { System.out.print((char)('A'+Math.abs(j-i))); } System.out.println(); } } }
5、小蓝有很多数字卡片,每张卡片上都是数字0到9。小蓝准备用这些卡片来拼一些数,他想从1开始拼出正整数,每拼一个,就保存起来,卡片就不能用来拼其它数了。小蓝想知道自己能从1拼到多少。例如,当小蓝有30张卡片,其中0到9各3张,则小蓝可以拼出1到10,但是拼11时卡片1已经只有一张了,不够拼出11。现在小蓝手里有0到9的卡片各2021张,共20210张,请问小蓝可以从1拼到多少?

import java.util.Scanner; // 1:无需package // 2: 类名必须Main, 不可修改 public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); //在此输入您的代码... int num1 = 0; for(int i=1;;i++){ int j=i; while(j>0){ if(j%10==1){ num1++; } j/=10; } if(num1==2021){ System.out.println(i); break; } } scan.close(); } }
6、小蓝有一个超大的仓库,可以摆放很多货物。现在,小蓝有 n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、 宽、高。小蓝希望所有的货物最终摆成一个大的立方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足 n = L × W × H。给定 n,请问有多少种堆放货物的方案满足要求。例如,当 n = 4 时,有以下 6 种方案:1×1×4、1×2×2、1×4×1、2×1×2、2 × 2 × 1、4 × 1 × 1。请问,当 n = 2021041820210418 (注意有 16 位数字)时,总共有多少种方案?

public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); long n = 2021041820210418l; int count = 0; ArrayList<Long> arr = new ArrayList<>(); for(long i=1;i<Math.sqrt(n);i++){ if(n%i==0){ arr.add(i); if(n/i!=i){ arr.add(n/i); } } } for(long i:arr){ for(long j:arr){ for(long k:arr){ if(i*j*k == n){ count++; } } } } System.out.println(count); scan.close(); } }
7、2,3,5,7,11,13,.... 是素数序列。 类似:7,37,67,97,127,1577,37,67,97,127,157 这样完全由素数组成的等差数列,叫等差素数数列。上边的数列公差为 30,长度为 6。2004 年,格林与华人陶哲轩合作证明了:存在任意长度的素数等差数列。 这是数论领域一项惊人的成果!有这一理论为基础,请你借助手中的计算机,满怀信心地搜索:长度为 10 的等差素数列,其公差最小值是多少?

public class Main { public static void main(String[] args) { for(int i=1;i<10000;i++){ for(int d=1;d<1000;d++){ int k; for(k=0;k<10;k++){ if(!IsPrime(i+d*k)){ break; } } if(k==10){ System.out.println(d); return; } } } } public static boolean IsPrime(int n){ for(int i=2;i<=Math.sqrt(n);i++){ if(n%i==0) return false; } return true; } }
8、小蓝在一个 n 行 m 列的方格图中玩一个游戏。开始时,小蓝站在方格图的左上角,即第 1 行第 1 列。小蓝可以在方格图上走动,走动时,如果当前在第 r 行第 c 列,他不能走到行号比 r 小的行,也不能走到列号比 c 小的列。同时,他一步走的直线距离不超过 3。例如,如果当前小蓝在第 3 行第 5 列,他下一步可以走到第 3 行第 6 列、第 3 行第 7 列、第 3 行第 8 列、第 4 行第 5 列、第 4 行第 6 列、第 4 行第 7 列、第 5 行第 5 列、第 5 行第 6 列、第 6 行第 5 列之一。小蓝最终要走到第 n 行第 m 列。在图中,有的位置有奖励,走上去即可获得,有的位置有惩罚,走上去就要接受惩罚。奖励和惩罚最终抽象成一个权值,奖励为正,惩罚为负。小蓝希望,从第 1 行第 1 列走到第 n 行第 m 列后,总的权值和最大。请问最大是多少?
输入描述
输入的第一行包含两个整数 n, m,表示图的大小。接下来 n 行,每行 m 个整数,表示方格图中每个点的权值。其中,1≤n≤100,−104 ≤权值≤104 。
输出描述
输出一个整数,表示最大权值和。

public class Main { static Scanner scan = new Scanner(System.in); static int n = scan.nextInt(); static int m = scan.nextInt(); static int[][] arr = new int[n][m]; static int dx[] = {0,0,0,1,2,3,1,2,1}; static int dy[] = {1,2,3,0,0,0,1,1,2}; static int max_length = -10000; public static void main(String[] args) { for(int i=0;i<n;i++){ for(int j=0;j<m;j++){ arr[i][j] = scan.nextInt(); } } dfs(0,0,arr[0][0]); System.out.println(max_length); } public static void dfs(int i,int j,int length){ if(i==n-1&&j==m-1) { max_length = Math.max(length, max_length); } for(int k=0;k<dx.length;k++) { int nx = i+dx[k]; int ny = j+dy[k]; if(nx>=0 && ny>=0 && nx<n && ny<m) { dfs(nx,ny,length+arr[nx][ny]); } } } }
9、如果一个质数 P 的每位数字都是质数, 而且每两个相邻的数字组成的两位 数是质数, 而且每三位相邻的数字组成的三位数是质数, 依次类推, 如果每相 邻的 k 位数字组成的 k 位数都是质数, 则 P 称为超级质数。如果把超级质数 P 看成一个字符串, 则这个超级质数的每个子串都是质数。例如, 53 是一个超级质数。请问, 最大的超级质数是多少?

import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); String s = ""; int max = 0; for(int i=1000000;i>1;i--) { if(Judge(i)) { max = Math.max(max, i); } } System.out.println(max); } //判断是否为超级质数 public static boolean Judge(int n) { String s = n+""; for(int i=0;i<s.length();i++) { for(int j=i;j<s.length();j++) { if(!IsPrime(s.substring(i, j+1))) { return false; } } } return true; } //判断是否为质数 public static boolean IsPrime(String s) { int n = Integer.parseInt(s); if(n==1) return false; for(int i=2;i<=Math.sqrt(n);i++) { if(n%i == 0) { return false; } } return true; } }
10、小蓝要和朋友合作开发一个时间显示的网站。在服务器上,朋友已经获取了当前的时间,用一个整数表示,值为从 1970 年 1 月 1 日 00:00:00 到当前时刻经过的毫秒数。现在,小蓝要在客户端显示出这个时间。小蓝不用显示出年月日,只需要显示出时分秒即可,毫秒也不用显示,直接舍去即可。给定一个用整数表示的时间,请将这个时间对应的时分秒输出。
输入描述
输入一行包含一个整数,表示时间。
输出描述
输出时分秒表示的当前时间,格式形如 HH:MM:SS,其中 HH 表示时,值为 0 到 23,MM 表示分,值为 0 到 59,S 表示秒,值为 0 到 59。时、分、秒 不足两位时补前导 0。

public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); long n = scan.nextLong(); scan.close(); long allseconds = n/1000; long seconds = allseconds%60; long allminutes = allseconds/60; long minutes = allminutes%60; long allhours = allminutes/60; long hours = allhours%24; String date = String.format("%02d", hours)+ ":"+String.format("%02d", minutes)+ ":"+String.format("%02d", seconds); System.out.println(date); } }
11、有 n 位同学同时找老师答疑。每位同学都预先估计了自己答疑的时间。老师可以安排答疑的顺序,同学们要依次进入老师办公室答疑。 一位同学答疑的过程如下:首先进入办公室,编号为 i 的同学需要 si 毫秒的时间。然后同学问问题老师解答,编号为 i 的同学需要ai 毫秒的时间。答疑完成后,同学很高兴,会在课程群里面发一条消息,需要的时间可 以忽略。最后同学收拾东西离开办公室,需要 ei 毫秒的时间。一般需要 10 秒、20 秒或 30 秒,即 ei 取值为 10000,20000 或 30000。一位同学离开办公室后,紧接着下一位同学就可以进入办公室了。答疑从 0 时刻开始。老师想合理的安排答疑的顺序,使得同学们在课程群 里面发消息的时刻之和最小。
输入描述
输入第一行包含一个整数 n,表示同学的数量。接下来 n 行,描述每位同学的时间。其中第 i 行包含三个整数 si, ai, ei,意义如上所述。其中有 ,1≤n≤1000,1≤si≤60000,1≤ai≤106,ei∈10000,20000,30000,即ei 一定是 10000、20000、30000之一。
输出描述
输出一个整数,表示同学们在课程群里面发消息的时刻之和最小是多少。

import java.util.*; public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); int n = scan.nextInt(); int[][] people = new int[n][3]; for(int i=0;i<n;i++) { people[i][0] = scan.nextInt(); people[i][1] = scan.nextInt(); people[i][2] = scan.nextInt(); } Arrays.sort(people,(a,b)->a[0]+a[1]+a[2]-b[0]-b[1]-b[2]); long sum = 0,time = 0; for(int i=0;i<n;i++) { time += people[i][0]+people[i][1]; sum += time; time +=people[i][2]; } System.out.println(sum); scan.close(); } }
12、到x星球旅行的游客都被发给一个整数,作为游客编号.x星的国王有个怪癖,他只喜欢数字3,5和7。国王规定,游客的编号如果只含有因子:3,5,7,就可以获得一份奖品。我们来看前10个幸运数字是:3579 15 21 25 27 35 45。因而第1个幸运数字是:49。小明领到了一个幸运数字59084709587505,他去领奖的时候,人家要求他准确地说出这是第几个幸运数字,否则领不到奖品。请你帮小明计算一下,59084709587505是第几个幸运数字。

public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); long num = 59084709587505l; int count = 0; for(int i=0;Math.pow(3, i)<num;i++) { for(int j=0;Math.pow(5, j)<num;j++) { for(int k=0;Math.pow(7, k)<num;k++) { if(Math.pow(3, i)*Math.pow(5, j)*Math.pow(7, k) < num) { count++; } } } } System.out.println(count); } }
13、小蓝学习了最短路径之后特别高兴,他定义了一个特别的图,希望找到图中的最短路径。小蓝的图由 2021 个结点组成,依次编号 1 至 2021 。对于两个不同的结点 a , b,如果 a 和 b 的差的绝对值大于 21 ,则两个结点之间没有边相连;如果 a 和 b 的差的绝对值小于等于 21,则两个点之间有一条长度为 a 和 b 的最小公倍数的无向边相连。例如:结点 1 和结点 23 之间没有边相连;结点 3 和结点 24 之间有一条无向边,长度为 24 ;结点 15 和结点 25 之间有一条无向边,长度为 75 。请计算,结点 1 和结点 2021 之间的最短路径长度是多少。

public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); int[] arr = new int[2022]; for(int i=2;i<=2021;i++) { arr[i] = Integer.MAX_VALUE; } for(int i=1;i<=2020;i++) { for(int j=i+1;(j<=2021) && (j-i<=21);j++) { arr[j] = Math.min(arr[j], arr[i]+len(i,j)); } } System.out.println(arr[2021]); } public static int gcd(int a,int b) { return b!=0 ? gcd(b,a%b):a; } public static int len(int a,int b) { return a*b/gcd(a,b); } }
14、把 2019分解成 3 个各不相同的正整数之和,并且要求每个正整数都不包含数字 2 和 4,一共有多少种不同的分解方法?注意交换 3个整数的顺序被视为同一种方法,例如 1000+1001+18和 1001+1000+18 被视为同一种。

public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); int n = 2019,count = 0; for(int i=1;i<n/3;i++) { for(int j=i+1;j<n;j++) { int k = 2019-i-j; if(!Have2and4(i) && !Have2and4(j) && !Have2and4(k) && (i<j) && (j<k)) { count++; } } } System.out.println(count); } public static boolean Have2and4(int n) { while(n>0) { if(n%10==2||n%10==4) { return true; } n/=10; } return false; } }
15、你一定听说过这个故事。国王对发明国际象棋的大臣很佩服,问他要什么报酬,大臣说:请在第 1个棋盘格放 1 粒麦子,在第 2 个棋盘格放 2 粒麦子,在第 3 个棋盘格放 4 粒麦子,在第 4 个棋盘格放 8 粒麦子,......后一格的数字是前一格的两倍,直到放完所有棋盘格(国际象棋共有 64 格)。国王以为他只是想要一袋麦子而已,哈哈大笑。当时的条件下无法准确计算,但估算结果令人吃惊:即使全世界都铺满麦子也不够用!请你借助计算机准确地计算,到底需要多少粒麦子。

import java.math.BigInteger; import java.util.*; public class Main { public static void main(String[] args) { BigInteger a = new BigInteger("0"); BigInteger b = new BigInteger("2"); for(int i=0;i<64;i++) { a = a.add(b.pow(i)); } System.out.println(a); } }
16、你有一架天平和 N 个砝码,这 N 个砝码重量依次是 W1,W2,⋅⋅⋅,WN。请你计算一共可以称出多少种不同的重量?注意砝码可以放在天平两边。
输入格式
输入的第一行包含一个整数 N。第二行包含 N 个整数:W1,W2,W3,⋅⋅⋅,WN。
输出格式
输出一个整数代表答案。
数据范围
对于 50% 的评测用例,1≤N≤15。对于所有评测用例,1≤N≤100,N个砝码总重不超过 10^5。

import java.util.*; public class Main { public static void main(String[] args) { Scanner scan = new Scanner(System.in); int n = scan.nextInt(); int[] arr = new int[n]; Set<Integer> set = new HashSet<>(); for(int i=0;i<n;i++) { arr[i] = scan.nextInt(); } set.add(0); for(int i=0;i<n;i++) { List<Integer> list = new ArrayList<>(set); for(int j : list) { set.add(arr[i]+j); set.add(Math.abs(arr[i]-j)); } } System.out.println(set.size()-1); } }
17、小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456 等。顺子日 期指的就是在日期的 yyyymmdd 表示法中,存在任意连续的三位数是一个顺 子的日期。例如 20220123 就是一个顺子日期,因为它出现了一个顺子:123; 而 20221023 则不是一个顺子日期,它一个顺子也没有。小明想知道在整个 2022 年份中,一共有多少个顺子日期。

public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int count = 0; for(int i=20220101;i<=20221231;i++) { if(Judge(i)) { if(IsSunZi(i)) { count++; } } } System.out.println(count); } //判断日期是否合法 public static boolean Judge(int n) { int[] arr = {31,28,31,30,31,30,31,31,30,31,30,31}; int month = n%10000/100; int day = n%100; if(day<=arr[month-1]) { return true; } return false; } public static boolean IsSunZi(int n) { String[] str = {"012","123","234","345","456","567","678","789"}; String s = n+""; for(int i=0;i<str.length;i++) { if(s.contains(str[i])) { return true; } } return false; } }
18、给10行数据,每行有10个整数,请你求出它们的乘积的末尾有多少个零?
输入格式
给10行数据,每行有10个整数。
输出格式
输出一个整数表示答案。

import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int two=0,five=0; int[] arr = new int[100]; for(int i=0;i<100;i++) { arr[i] = sc.nextInt(); } for(int i=0;i<100;i++) { int t = arr[i]; while(t%2 == 0) { t/=2; two++; } while(t%5 == 0) { t/=5; five++; } } System.out.println(Math.min(two, five)); } }
19、小蓝对一个数的数位之和很感兴趣,今天他要按照数位之和给数排序。当两个数各个数位之和不同时,将数位和较小的排在前面,当数位之和相等时,将数值小的排在前面。例如,2022 排在 409 前面,因为 2022 的数位之和是 6,小于 409 的数位之和 13。又如,6 排在 2022 前面,因为它们的数位之和相同,而 6 小于 2022。给定正整数 n,m,请问对 1到 n 采用这种方法排序时,排在第 m个的元素是多少?
输入格式
输入第一行包含一个正整数 n。第二行包含一个正整数 m。
输出格式
输出一行包含一个整数,表示答案。

import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int m= sc.nextInt(); Integer[] arr = new Integer[n]; for(int i=0;i<n;i++) { arr[i] = i+1; } Arrays.sort(arr, (o1,o2)->Sum(o1)!=Sum(o2) ? Sum(o1)-Sum(o2):o1-o2); System.out.println(arr[m-1]); } public static int Sum(int n) { int sum = 0; while(n>0) { sum+= n%10; n/=10; } return sum; } }
20、小蓝负责一个公司的考勤系统, 他每天都需要根据员工刷卡的情况来确定 每个员工是否到岗。当员工刷卡时, 会在后台留下一条记录, 包括刷卡的时间和员工编号, 只 要在一天中员工刷过一次卡, 就认为他到岗了。现在小蓝导出了一天中所有员工的刷卡记录, 请将所有到岗员工的员工编 号列出。
输入格式
输入的第一行包含一个正整数 n , 表示一天中所有员工的刷卡记录的条数。 接下来 n 行, 每行包含一条刷卡记录, 每条刷卡记录的格式为:HH:MM:SS ID。其中 HH:MM: SS 表示刷卡时间, HH 为一个 0 到 23 之间的两位十进制整数 (可能含前导 0 ) 表示时, MM 为一个 0 到 59 之间的两位十进制整数 (可能含前 导 0) 表示分, SS 为一个 0 到 59 之间的两位十进制整数 (可能含前导 0 ) 表 示秒, ID 为一个不含前导 0 的整数表示员工的编号。所有记录按照刷卡时间升序排列, 可能同一时刻有多人刷卡。
输出格式
输出若干行, 每行包含一个整数, 按照从小到大的顺序输出, 表示到岗员 工的编号。

import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); String[] str = new String[n*2]; for(int i=0;i<n*2;i++) { str[i] = sc.next(); } //TreeSet有顺序的去重集合容器 TreeSet<Integer> set = new TreeSet<>(); for(int i=1;i<n*2;i+=2) { set.add(Integer.parseInt(str[i])); } for(int i:set) { System.out.println(i); } } }
21、给定正整数n,请问有多少个质数是n的约数。
输入格式
输入的第一行包含一个整数 n 。
输出格式
输出一个整数, 表示 n 的质数约数个数。

public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); long n = sc.nextLong(); int count=0; //任何一个合数都可以被分解为几个质数相乘 for(long i=2;i<=Math.sqrt(n);i++) { if(n%i == 0) { count++; } while(n%i == 0) { n/=i; } } if(n>1) { count++; } System.out.println(count); } }
22、给定两个不同的正整数a, b,求一个正整数k使得gcd(a + k, b + k)尽可能大。其中gcd(a, b)表示a和b的最大公约数,如果存在多个k,请输出所有满足条件的k中最小的那个。

import java.util.*; /*对于a<=b,有gcd(a,b)=gcd(a,b-a) 所以gcd(a+k,b+k)=gcd(a+k,b-a) 设c=b-a c是已知的,所以想要使得a+k与c的最大公因子尽可能地大 最大能到达c 显然这个式子的最大gcd一定为 c ,我们只需要计算出a 最少需要增加多少可以成为 c 的倍数,这个增量即是答案k */ public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); long a = sc.nextLong(); long b = sc.nextLong(); long c = Math.abs(a-b); if(c<a) { c = (a/c+1)*c; } long k = c-a; System.out.print(k); } }
23、


import java.util.*; /*假定4个数排序, 正排序:1,2,3,4价值和为6,反排序:4,3,2,1的价值和为0 正排序:1,3,2,4价值和为5,反排序:4,2,3,1的价值和为1 依次推下去就会发现这种正排序和对应的反排序的价值和相加为一个定值6,所以4个数排序就是24种排序方式,12对排列式,价值和也就有12个6,总价值和就是72 所以当输入n个数时就有n!/2 对排列式,而我们可以靠第一个正排序就能推出这个定值价值和,就是0+1+2+3,一对排列式的价值和就是n(n-1)/2 ,那么总价值和为 n!*n(n-1)/4 */ public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); long n = sc.nextLong(); long num = 998244353l; long result = n*(n-1)/2; for(int i=1;i<n+1;i++) { if(i!=2) result = (result*i)%num; } System.out.println(result); } }
24、在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上,那么这些点中任意两点确定的直线是同一条。给定平面上2 × 3个整点{(x, y)|0 ≤ x < 2, 0 ≤ y < 3, x ∈ Z, y ∈ Z},即横坐标是0到 1 (包含 0 和 1) 之间的整数、纵坐标是 0 到 2 (包含0和 2) 之间的整数的点。这些点一共确定了 11 条不同的直线。给定平面上 20× 21 个整点{(x, y)|0 ≤ x < 20, 0 ≤ y < 21, x ∈ Z, y ∈ Z},即横坐标是 0到 19 (包含 0 和 19) 之间的整数、纵坐标是 0 到 20(包含 0 和 20) 之间的整数的点。请问这些点一共确定了多少条不同的直线。

import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); Set<String> set = new HashSet<>(); for(int x1=0;x1<20;x1++) { for(int y1=0;y1<21;y1++) { for(int x2=0;x2<20;x2++) { for(int y2=0;y2<21;y2++) { if(x1==x2 || y1==y2) { continue; } int y = y2-y1; int x = x2-x1; int d = gcd(x,y); String k = y/d+ "/" +x/d; int m = y2*x1-y1*x2; int n = gcd(m,x); String b = m/n+ "/" +x/n; set.add(k+" "+b); } } } } System.out.println(set.size()+20+21); } public static int gcd(int a,int b) { return a%b==0 ? b:gcd(b,a%b); } }
25、给定一个单词,请问在单词中删除 t 个字母后,能得到的字典序最小的单词是什么?输入的第一行包含一个单词,由大写英文字母组成。第二行包含一个正整数 t。其中,单词长度不超过 100100,t 小于单词长度。输出一个单词,表示答案。

import java.util.*; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); String s = sc.next(); int t = sc.nextInt(); char[] c = s.toCharArray(); ArrayList<Character> list = new ArrayList<>(); for(int i=0;i<s.length();i++) { list.add(c[i]); if(list.size()>1 && t>0) { list.remove(list.indexOf(Collections.max(list))); t--; } } for(char l : list) { System.out.print(l); } } }
26、你有一架天平。现在你要设计一套砝码,使得利用这些砝码可以称出任意 小于等于 N 的正整数重量。那么这套砝码最少需要包含多少个砝码?注意砝码可以放在天平两边。

import java.util.*; /*结果应该是最少的砝码数量 首先,如果要称的重量为1的话,只能选择重量为1的砝码,1是必选的一个砝码。 然后再称比1重的,反正都是要再加砝码,那我们为何不选一个能称的重量尽可能大的呢。 选1、2的砝码可以满足1=1,2=2,1+2=3 选1、3的砝码可以满足1=1,2=3-1,3=3,4=3+1 选1、4的砝码可以满足1=1,2=?无法称2,不合题意 因此我们选择的砝码组合是1、3,此时我们可以称的最大重量为4 当我们还需要再增加砝码时 同理可得 选1、3、9的组合可以满足小于等于13(13=1+3+9)的所有重量 比如说我定义的砝码是1 3 9 3n 1砝码的最大重量值 1 2砝码的最大重量值 4 3 13 */ public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); long n = sc.nextLong(); long num = 1; long sum = 1; while(sum<n) { num++; sum = sum*3+1; } System.out.println(num); } }
27、小明冒充 X 星球的骑士,进入了一个奇怪的城堡。城堡里边什么都没有,只有方形石头铺成的地面。 假设城堡地面是n×n 个方格。如下图所示。
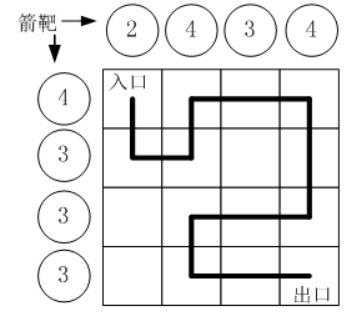
按习俗,骑士要从西北角走到东南角。可以横向或纵向移动,但不能斜着走,也不能跳跃。每走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有 n 个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。本题的要求就是已知箭靶数字,求骑士的行走路径(测试数据保证路径唯一)
输入描述
第一行一个整数 N (0≤N≤20),表示地面有N×N 个方格。第二行 N 个整数,空格分开,表示北边的箭靶上的数字(自西向东)。第三行 N 个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出描述
输出一行若干个整数,表示骑士路径。为了方便表示,我们约定每个小格子用一个数字代表,从西北角开始编号: 0,1,2,3 ⋯⋯
比如,上图中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15

import java.util.*; public class Main { static int[] path;//记录行走的路径 static int n; static int[] north;//北面箭数 static int[] west;//西面箭数 static boolean[][] visited; static boolean success; static int dx[] = {1,0,-1,0}; static int dy[] = {0,1,0,-1}; public static void main(String[] args) { Scanner sc = new Scanner(System.in); n = sc.nextInt(); north = new int[n]; west = new int[n]; path = new int[n*n]; visited = new boolean[n][n]; for(int i=0;i<n;i++) { north[i] = sc.nextInt(); } for(int i=0;i<n;i++) { west[i] = sc.nextInt(); } dfs(0,0,0); } public static void dfs(int x,int y,int step) { path[step] = n*y+x;//将当前编号添加到路径 visited[x][y] = true; north[x]--; west[y]--; if(x==n-1 && y==n-1 && check()) { success = true; for(int i=0;i<=step;i++) { System.out.print(path[i]+" "); } return; } for(int i=0;i<4;i++) { int xx = x+dx[i]; int yy = y+dy[i]; if(!success && xx>=0 && xx<=n-1 && yy>=0 && yy<=n-1 && !visited[xx][yy]) { if(north[xx]>0 && west[yy]>0) { dfs(xx,yy,step+1); visited[xx][yy] = false; north[xx]++; west[yy]++; } } } } public static boolean check() {//判断是否还有剩余的箭 for(int i=0;i<n;i++) { if(north[i]!=0 || west[i]!=0) { return false; } } return true; } }
28、定义阶乘 n!=1×2×3×⋅⋅⋅×n。请问 100!(100 的阶乘)有多少个正约数。

/** * 任意一个正整数x都可以表示成若干个质数乘机的形式 * 最后的结果就是质因子的出现次数+1之后连乘即可 * 正约数个数=(a1+1)*(a2+1)...(an+1),a1,a2,an分别是各个质因子的出现次数 * 比如8=2*2*2, 约数为1,2,4,8 正约数=(3+1)=4 * 比如180=2*2*3*3*5 则正约数=(2+1)*(2+1)*(1+1)=18 * */ public class Main { public static int[] arr; public static long sum=1; public static void main(String[] args) { arr = new int[101]; for (int i = 2; i <=100 ; i++) { zhiyin(i); } for (int i = 2; i <=100; i++) { if(arr[i]!=0){ sum*=(arr[i]+1); } } System.out.println(sum); } //统计n的质因数出现次数,并用arr数组记录 public static void zhiyin(int n){ int i=2; while(n!=1){ if(n%i==0&&isPrime(i)){ arr[i]++; n/=i; }else{ i++; } } } public static boolean isPrime(int x){ if(x==0||x==1){ return false; } for (int i = 2; i <=Math.sqrt(x) ; i++) { if(x%i==0){ return false; } } return true; } }
29、小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有 N 种蒸笼,其中第 i 种蒸笼恰好能放 Ai 个包子。每种蒸笼都有非常多笼,可以认为是无限笼。每当有顾客想买 X 个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有 X 个包子。比如一共有 3 种蒸笼,分别能放 3、4 和 5 个包子。当顾客想买 11 个包子时,大叔就会选 2 笼 3 个的再加 1 笼 5 个的(也可能选出 1 笼 3 个的再加 2 笼 4 个的)。当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有 3 种蒸笼,分别能放 4、5 和 6 个包子。而顾客想买 7 个包子时,大叔就凑不出来了。小明想知道一共有多少种数目是包子大叔凑不出来的。
输入描述
第一行包含一个整数 N (1≤N≤100)。
以下 N 行每行包含一个整数 Ai (1≤Ai≤100)。
输出描述
一个整数代表答案。如果凑不出的数目有无限多个,输出 INF。

import java.util.*; public class Main { static int g; public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int[] arr = new int[n]; boolean dp[] = new boolean[10001]; for(int i=0;i<n;i++) { arr[i] = sc.nextInt(); if(i==0) { g = arr[0]; } g = gcd(g,arr[i]); } if(g!=1) { //所有系数不互质,解有无数个。 System.out.println("INF"); } else { for(int i=0;i<n;i++) { for(int j=1;j<dp.length;j++) { if(j%arr[i] == 0) { dp[j] = true; } } } for(int i=1;i<n;i++) { for(int j=1;j<dp.length;j++) { if(dp[j] && j+arr[i]<dp.length) { //在能凑出来的情况下,他的下一个能凑出来的个数是 //一种笼子里面的包子数加上当前能凑出来的个数是一定能凑出来的 dp[j+arr[i]] = true; } } } } int count = 0; for(int i=1;i<dp.length;i++) { if(!dp[i]) { count++; } } System.out.println(count); } public static int gcd(int a,int b) { return a%b==0 ? b:gcd(b,a%b); } }
30、考虑一种简单的正则表达式:只由 x ( ) | 组成的正则表达式。小明想求出这个正则表达式能接受的最长字符串的长度。例如 ((xx|xxx)x|(x|xx))xx 能接受的最长字符串是: xxxxxx,长度是 6。
输入描述
一个由 x()| 组成的正则表达式。输入长度不超过 100,保证合法。
输出描述
这个正则表达式能接受的最长字符串的长度。

import java.util.*; public class Main { public static String s; public static int pos = -1; public static void main(String[] args) { Scanner sc = new Scanner(System.in); s = sc.next(); System.out.println(dfs()); } public static int dfs() { int current = 0; int max = 0; while(pos < s.length()-1) { pos++; if(s.charAt(pos) == '(') { current += dfs(); } else if(s.charAt(pos) == 'x') { current++; } else if(s.charAt(pos) == '|') { max = Math.max(max, current); current = 0; } else { break; } } return Math.max(max, current); } }




