算法分析-寻找假币题

一.题目需求

你手里有70枚重量相等的真金硬币，但你知道其中有一枚是假币，比其他金币轻。
你有一个平衡秤，你可以一次在两边放上任意数量的硬币，它会告诉你两边是否重量相同，或者如果不相同，哪边更轻。
问题：请概述一个寻找假币的算法。你需要称量多少次？怎么使得称量次数最少？

二、算法思想

1.算法分析
1.1. 这个问题可以使用分治算法来解决。
1.2. 我们可以将硬币分成三组，如70枚，先分成，前两组包含23枚硬币，第三组含24枚硬币。
1.3. 然后我们使用平衡秤先称量前两组硬币，如果两边重量相同，那么假币就在剩下的第三组中。然后递归上述操作。
1.4. 如果两边重量不同，那么假币就在较轻的那一边。然后递归上述操作，直到最后只有1枚时，即可找到假币。

三、代码展示
1.天枰称量方法
输入两组硬币列表参数，比较两组总数量值，返回左右哪组轻，或相等：

def balance_scale(group1, group2):
    total1 = sum(group1)
    total2 = sum(group2)

    if total1 < total2:
        return "left"
    elif total1 > total2:
        return "right"
    else:
        return "equal"

2.寻找假币方法

1.1. 采用三分法，寻找假币。
1.2. 我们可以将硬币分成三组，如70枚，先分成，前两组包含23枚硬币，第三组含24枚硬币。
1.3. 然后我们使用平衡秤先称量前两组硬币，如果两边重量相同，那么假币就在剩下的第三组中。然后递归上述操作。
1.4. 如果两边重量不同，那么假币就在较轻的那一边。然后递归上述操作，直到最后只有1枚时，即可找到假币。

def find_fake_coin_by_three_partition(coin_list):
    '''
    @方法名称: 三分法，寻找假币方法
    @中文注释: 三分法，寻找假币方法
        我们可以将硬币分成三组，前两组包含23枚硬币，第三组含24枚硬币。
        然后我们使用平衡秤先称量前两组硬币，如果两边重量相同，那么假币就在剩下的第三组中；
        如果两边重量不同，那么假币就在较轻的那一边。依次类推即可找到假币。
    @入参:
        @param coin_list list 硬币列表
    @出参:
        @param count int 称量次数
    @作    者: PandaCode辉
    @weixin公众号: PandaCode辉
    @创建时间: 2023-11-28
    @使用范例: find_fake_coin_by_three_partition([1,1,1,1,0,1,1])
    '''
    print('=====================')
    # 硬币列表最后只剩1枚时，即找到假币，结束
    if len(coin_list) == 1:
        return 1
    # 硬币列表最后只剩2枚时
    elif len(coin_list) == 2:
        print(coin_list)
        # 还剩2枚，再分2组，再称量一次
        print('还剩2枚，再分2组，再称量一次')
        group_size = 1
        group1 = coin_list[:group_size]
        group2 = coin_list[group_size:]
        result = balance_scale(group1, group2)
        return find_fake_coin_by_three_partition(group1 if result == "left" else group2) + 1
    else:
        # 将硬币列表，三等分大小
        group_size = len(coin_list) // 3
        # 前两组，硬币数量保持一致
        group1 = coin_list[:group_size]
        group2 = coin_list[group_size:2 * group_size]
        # 第三组，硬币数量，取最后剩余值
        group3 = coin_list[2 * group_size:]
        print(group1)
        print(group2)
        print(group3)
        # 天枰称量，前两组
        result = balance_scale(group1, group2)
        print(result)
        # 如果前两组重量相同，那么假币就在剩下的第三组中
        if result == "equal":
            return find_fake_coin_by_three_partition(group3) + 1
        else:
            # 如果前两组重量不同，那么假币就在较轻的那一边。
            return find_fake_coin_by_three_partition(group1 if result == "left" else group2) + 1

这个算法的时间复杂度是O(logn)。

时间复杂度分析：

这个算法使用了三分法来寻找假币。在每次递归调用中，硬币列表被分成三等分，然后进行称量。
这个过程会一直重复，直到只剩下一枚硬币为止。
因此，每一次递归调用都会将问题的规模减半，所以时间复杂度是O(logn)。这里的n是硬币列表的长度。

3.实现主函数

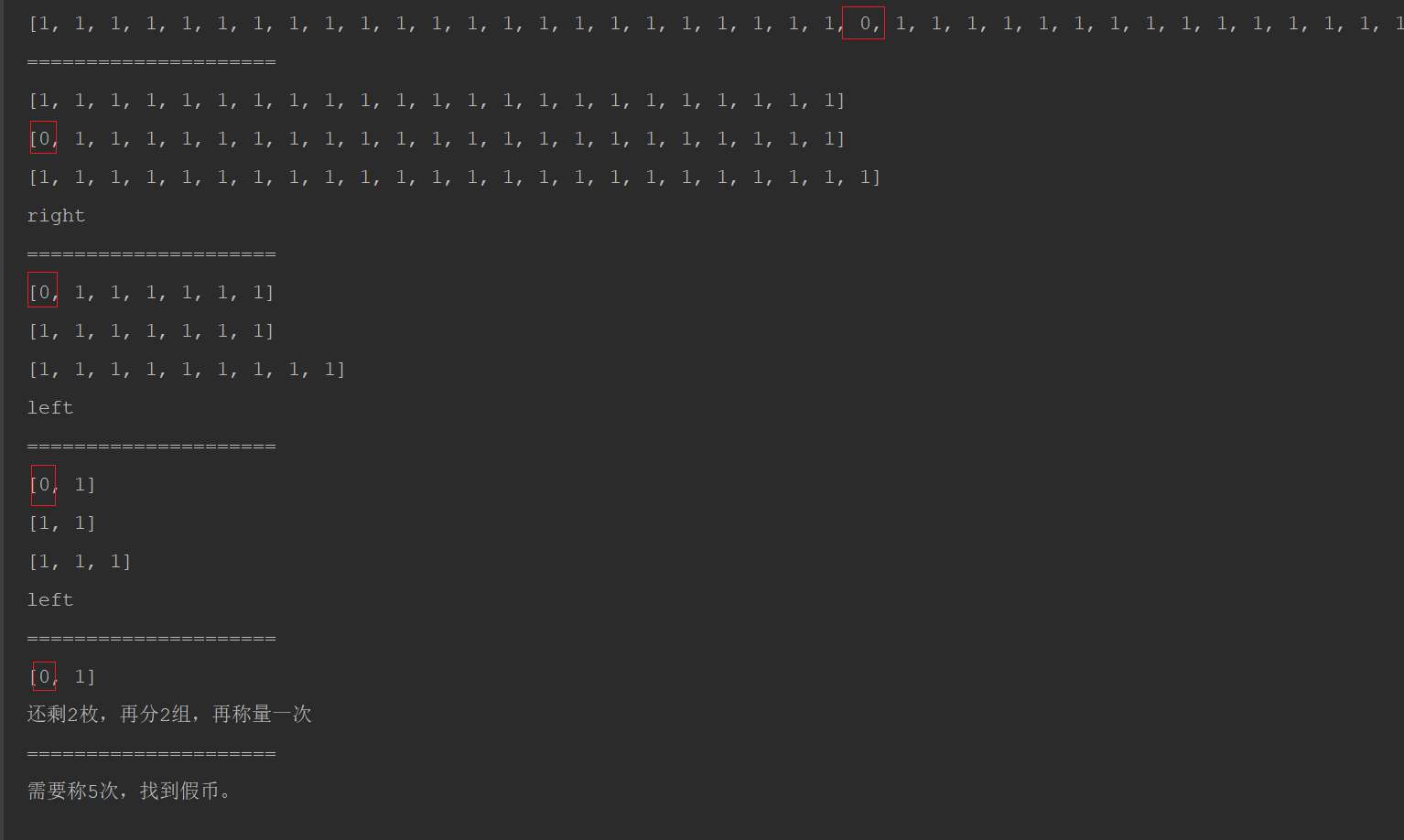
if __name__ == "__main__":
    # 假设有70枚真金硬币，1-为真币，其中一枚是假币,0-为假币
    coin_list = [1 for i in range(70)]
    # 随机选择一个索引，随机选择其中一枚设为假币
    random_index = random.randint(0, len(coin_list) - 1)
    # 修改选中的元素,0-为假币
    coin_list[random_index] = 0
    print(coin_list)
    print("需要称{}次，找到假币。".format(find_fake_coin_by_three_partition(coin_list)))

4.运行结果

从运行结果可以看出，只需称量5次，就能找到假币。

==========结束==========