[NOI2016][洛谷P1117]优秀的拆分(SA)
题面
https://www.luogu.com.cn/problem/P1117
题解
前置知识:
本题要求一个字符串中所有AABB形式的字符串(可重)的个数。
首先考虑简化要求:设f[x]表示以第x位为结尾,有多少个AA形式的字符串;g[x]表示以第x位为开头有多少个AA形式的字符串。答案显然是\(\sum f[i]g[i+1]\)。
枚举AA型字符串的半长len,然后设置第1位,第len+1位,第2len+1位…为特殊点。一个长度为2len的AA型字符串一定通过恰好两个相邻的特殊点。不妨设这两个点是i,j。
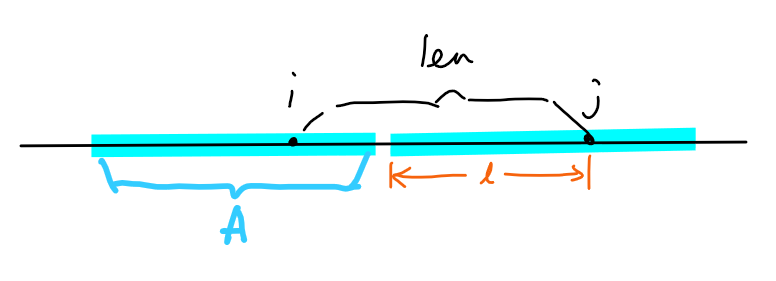
A在特殊点左边的部分长l(包括特殊点本身),那么显然有\(1{\leq}l{\leq}len\)。另外,i,j还必须满足\(lcs(pre_i,pre_j){\geq}l\)以及\(lcp(suf_i,suf_j){\geq}len-l+1\)。
所以通过两个相邻特殊点i、j,并且特殊点左边的部分长为l的、半长为len的AA型字符串存在的必要条件是:
\[\begin{cases} l{\geq}\max(1,len+1-lcp(suf_i,suf_j)) \\ l{\leq}\min(len,lcs(pre_i,pre_j)) \end{cases}
\]
不难发现这也是充分条件。
所以枚举了len,i,j之后,设\(high=\min(len,lcs(pre_i,pre_j)),low=\max(1,len+1-lcp(suf_i,suf_j))\),如果\(high{\leq}low\),就把i-high+1到i-low+1的g值全部++,把j+len-high到j+len-low的f值全部++。这个可以维护差分而做到\(O(1)\)的更新。
前缀的最长公共后缀、后缀的最长公共前缀都可以通过预处理前(后)缀数组+height数组上ST表做到O(1)。
所以总时间复杂度是调和级数\(O(\sum_{i=1}^{n}{\frac{n}{i}})=O(n \log n)\)。
代码
#include<bits/stdc++.h>
using namespace std;
#define rg register
#define In inline
#define ll long long
const int N = 30000;
In int read(){
int s = 0,ww = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')ww = -1;ch = getchar();}
while('0' <= ch && ch <= '9'){s = 10 * s + ch - '0';ch = getchar();}
return s * ww;
}
int n;
char s[N+5];
ll f[N+5],g[N+5];
int lg[N+5];
struct ST{
int minn[N+5][16];
void prepro(int a[]){
for(rg int i = 1;i <= n;i++)minn[i][0] = a[i];
for(rg int j = 1;j <= 15;j++)
for(rg int i = 1;i + (1<<j) - 1 <= n;i++)minn[i][j] = min(minn[i][j-1],minn[i+(1<<(j-1))][j-1]);
}
int query(int l,int r){
int d = lg[r-l+1];
return min(minn[l][d],minn[r+1-(1<<d)][d]);
}
};
struct SA{
int sa[N+5],rk[N+5],temp[N+5],num[N+5],h[N+5];
int m;
void clear(){
memset(sa,0,sizeof(int)*(n+2));
memset(rk,0,sizeof(int)*(n+2));
memset(temp,0,sizeof(int)*(n+2));
}
void qsort(){
memset(num,0,sizeof(int) * (m+1));
for(rg int i = 1;i <= n;i++)num[rk[i]]++;
for(rg int i = 2;i <= m;i++)num[i] += num[i-1];
for(rg int i = n;i >= 1;i--)sa[num[rk[temp[i]]]--] = temp[i];
}
ST H;
void calch(){
int k = 0;
for(rg int i = 1;i <= n;i++){
if(rk[i] == 1)h[1] = k = 0;
else{
if(k)k--;
int j = sa[rk[i]-1];
while(s[i+k] == s[j+k])k++;
h[rk[i]] = k;
}
}
}
void init(){
clear();
m = 26;
for(rg int i = 1;i <= n;i++)temp[i] = i;
for(rg int i = 1;i <= n;i++)rk[i] = s[i] - 'a' + 1;
qsort();
for(rg int d = 1;d <= n;d <<= 1){
int cnt = 0;
for(rg int i = n - d + 1;i <= n;i++)temp[++cnt] = i;
for(rg int i = 1;i <= n;i++)if(sa[i] > d)temp[++cnt] = sa[i] - d;
qsort();
memcpy(temp,rk,sizeof(int) * (n+1));
cnt = 1;
rk[sa[1]] = 1;
for(rg int i = 2;i <= n;i++){
if(temp[sa[i]] != temp[sa[i-1]] || temp[sa[i]+d] != temp[sa[i-1]+d])cnt++;
rk[sa[i]] = cnt;
}
if(cnt == n)break;
m = cnt;
}
calch();
H.prepro(h);
}
int lcp(int i,int j){
int x = rk[i],y = rk[j];
if(x > y)swap(x,y);
return H.query(x + 1,y);
}
}S;
struct PA{
int pa[N+5],rk[N+5],temp[N+5],num[N+5],h[N+5];
int m;
void clear(){
memset(pa,0,sizeof(int)*(n+2));
memset(rk,0,sizeof(int)*(n+2));
memset(temp,0,sizeof(int)*(n+2));
}
void qsort(){
memset(num,0,sizeof(int) * (m+1));
for(rg int i = 1;i <= n;i++)num[rk[i]]++;
for(rg int i = 2;i <= m;i++)num[i] += num[i-1];
for(rg int i = n;i >= 1;i--)pa[num[rk[temp[i]]]--] = temp[i];
}
ST H;
void calch(){
int k = 0;
for(rg int i = n;i >= 1;i--){
if(rk[i] == 1)h[1] = k = 0;
else{
if(k)k--;
int j = pa[rk[i]-1];
while(s[i-k] == s[j-k])k++;
h[rk[i]] = k;
}
}
}
void init(){
clear();
m = 26;
for(rg int i = 1;i <= n;i++)temp[i] = i;
for(rg int i = 1;i <= n;i++)rk[i] = s[i] - 'a' + 1;
qsort();
for(rg int d = 1;d <= n;d <<= 1){
int cnt = 0;
for(rg int i = 1;i <= d;i++)temp[++cnt] = i;
for(rg int i = 1;i <= n;i++)if(pa[i] + d <= n)temp[++cnt] = pa[i] + d;
qsort();
memcpy(temp,rk,sizeof(int) * (n+1));
cnt = 1;
rk[pa[1]] = 1;
for(rg int i = 2;i <= n;i++){
if(temp[pa[i]] != temp[pa[i-1]] || temp[pa[i]-d] != temp[pa[i-1]-d])cnt++;
rk[pa[i]] = cnt;
}
if(cnt == n)break;
m = cnt;
}
calch();
H.prepro(h);
}
int lcs(int i,int j){
int x = rk[i],y = rk[j];
if(x > y)swap(x,y);
return H.query(x + 1,y);
}
}P;
void calcfg(){
for(rg int len = 1;(len<<1) <= n;len++){
for(rg int i = 1;i + len <= n;i += len){
int j = i + len;
int high = P.lcs(i,j); high = min(high,len);
int low = S.lcp(i,j); low = max(len + 1 - low,1);
if(low <= high){
g[i-high+1]++;
g[i-low+2]--;
f[j+len-high]++;
f[j+len-low+1]--;
}
}
}
for(rg int i = 1;i <= n;i++)f[i] += f[i-1],g[i] += g[i-1];
}
int main(){
for(rg int i = 2;i <= N;i++)lg[i] = lg[i>>1] + 1;
int T = read();
while(T--){
scanf("%s",s + 1);
n = strlen(s + 1);
S.init();
P.init();
calcfg();
ll ans = 0;
for(rg int i = 1;i < n;i++)ans += f[i] * g[i+1];
cout << ans << endl;
memset(f,0,sizeof(ll) * (n+2));
memset(g,0,sizeof(ll) * (n+2));
}
return 0;
}

