[NOI2005][BZOJ1502][洛谷P4207]月下柠檬树(自适应Simpson积分)
题面
https://www.luogu.com.cn/problem/P4207
题解
前置知识
首先需要一些空间想象力~
1、圆形:一个空中的圆形, 其影子应该也是一个圆形。并且,其圆心距离树根的距离应该是原来高度的\(\cot \alpha\)倍。

2、圆台侧面:在画好圆台的上、下底面的影子以后,只需加上上、下底面的外公切线之间的部分。当然,如果上下底面内切甚至内含,圆台侧面的影子就整体被较大的那个圆覆盖了,此时没必要加任何东西。
所以,最终我们要计算面积的形状就是由所有的圆的影子,以及相邻两圆之间(如果外离)的两条外公切线组成的图形。
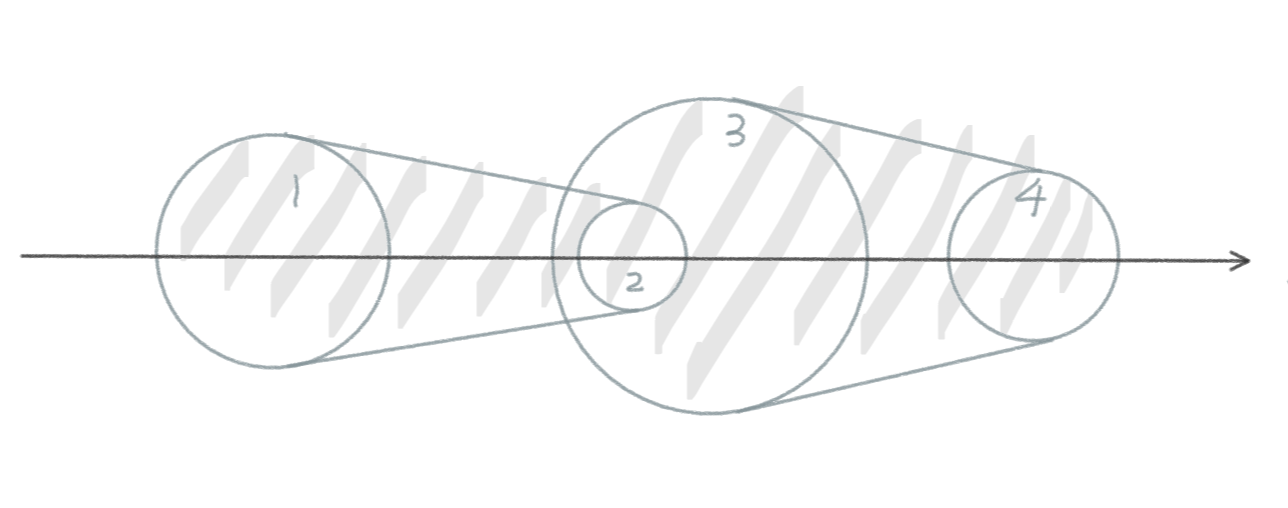
接下来只要使用自适应Simpson积分。实现时,可以只统计此图形的x轴以上的一半,最后再统一乘2。
Simpson中需要积分的函数f(x)即为横坐标x对应的高度。直接存下所有的半圆和外公切线段,然后一一判断其是否覆盖横坐标x;覆盖的话计算高度即可。
由于题目只需要1e-2的精度,本题eps我使用1e-7已经足够。
代码
#include<bits/stdc++.h>
using namespace std;
#define N 500
#define rg register
#define eps 1e-9
#define inf 1e9
#define In inline
In int sgn(double x){return x < -eps ? -1 : x > eps;}
In double sqr(double x){return x * x;}
struct vec{
double x,y;
vec(){}
vec(double _x,double _y){x = _x,y = _y;}
In friend vec operator + (vec a,vec b){
return vec(a.x + b.x,a.y + b.y);
}
In friend vec operator - (vec a,vec b){
return vec(a.x - b.x,a.y - b.y);
}
In friend double Dot(vec a,vec b){
return a.x * b.x + a.y * b.y;
}
In friend double Cross(vec a,vec b){
return a.x * b.y - a.y * b.x;
}
};
struct line{
vec p,q;
line(){}
line(vec _p,vec _q){p = _p,q = _q;}
In friend double Height(line a,double x){ //计算线段a在横坐标为x时的纵坐标值
if(sgn(x-a.p.x) < 0 || sgn(x-a.q.x) > 0)return 0;
return (a.q.y * (x-a.p.x) + a.p.y * (a.q.x-x)) / (a.q.x - a.p.x);
}
};
line l[N+5];
int ln;
struct cir{
double c,r;
cir(){}
cir(double _c,double _r){c = _c,r = _r;}
In friend double Height(cir a,double x){ //计算半圆a在横坐标为x时的纵坐标值
if(sgn(fabs(x-a.c)-a.r) >= 0)return 0;
return sqrt(sqr(a.r) - sqr(x-a.c));
}
In friend void CalcTan(cir a,cir b){ //计算半圆a,b的外公切线
if(sgn(fabs(a.c-b.c)-fabs(a.r-b.r)) <= 0)return;
if(sgn(a.c-b.c) > 0)swap(a,b);
if(sgn(a.r-b.r) == 0){
l[++ln] = line(vec(a.c,a.c+a.r),vec(b.c,b.c+b.r));
return;
}
double cs = ((a.r-b.r) / (b.c-a.c));
l[++ln] = line(vec(a.c+a.r*cs,a.r*sqrt(1-sqr(cs))),vec(b.c+b.r*cs,b.r*sqrt(1-sqr(cs))));
}
};
cir c[N+5];
int n;
double f(double x){
double ans = 0;
for(rg int i = 1;i <= ln;i++)ans = max(ans,Height(l[i],x));
for(rg int i = 1;i <= n;i++)ans = max(ans,Height(c[i],x));
return ans;
}
double Simp(double l,double r){
return (f(l) + 4 * f((l+r)/2) + f(r)) * (r - l) / 6;
}
double RSimp(double l,double r,double A,double Eps){
double m = (l + r) / 2;
double L = Simp(l,m),R = Simp(m,r);
if(fabs(L+R-A) <= Eps)return L + R + (L + R - A) / 15;
return RSimp(l,m,L,Eps) + RSimp(m,r,R,Eps);
}
double alpha;
int main(){
scanf("%d%lf",&n,&alpha);
double x = 0,h;
for(rg int i = 1;i <= n + 1;i++){
scanf("%lf",&h);
x += h / tan(alpha);
c[i].c = x;
}
for(rg int i = 1;i <= n;i++)scanf("%lf",&c[i].r);
c[n+1].r = 0;
for(rg int i = 1;i <= n;i++)CalcTan(c[i],c[i+1]);
double L = inf,R = 0;
for(rg int i = 1;i <= n + 1;i++){
L = min(L,c[i].c - c[i].r);
R = max(R,c[i].c + c[i].r);
}
printf("%.2lf\n",2 * RSimp(L,R,Simp(L,R),1e-7));
return 0;
}

