[USACO 2020.1 Platinum][LOJ3248]Falling Portals(凸包+树上倍增)
题面
题解
不妨设向下坠落的方向为正方向,那么世界i所处的位置为\(it-A[i](i{\geq}0)\)。那么我们可以画出各世界的S-t图像。
先考虑如果\(A[i]>A[Q[i]]\),即i需要追赶的情况。
如果射线i与射线j在某处相交,且j>i,那么我们称这个点是i的“向上拐点”,是j的“向下拐点”。

那么有性质1:从i出发,遇到向上拐点就拐,那么一定是一种最优方案。(如果遇到三线共点,走该处斜率最大的一条射线)
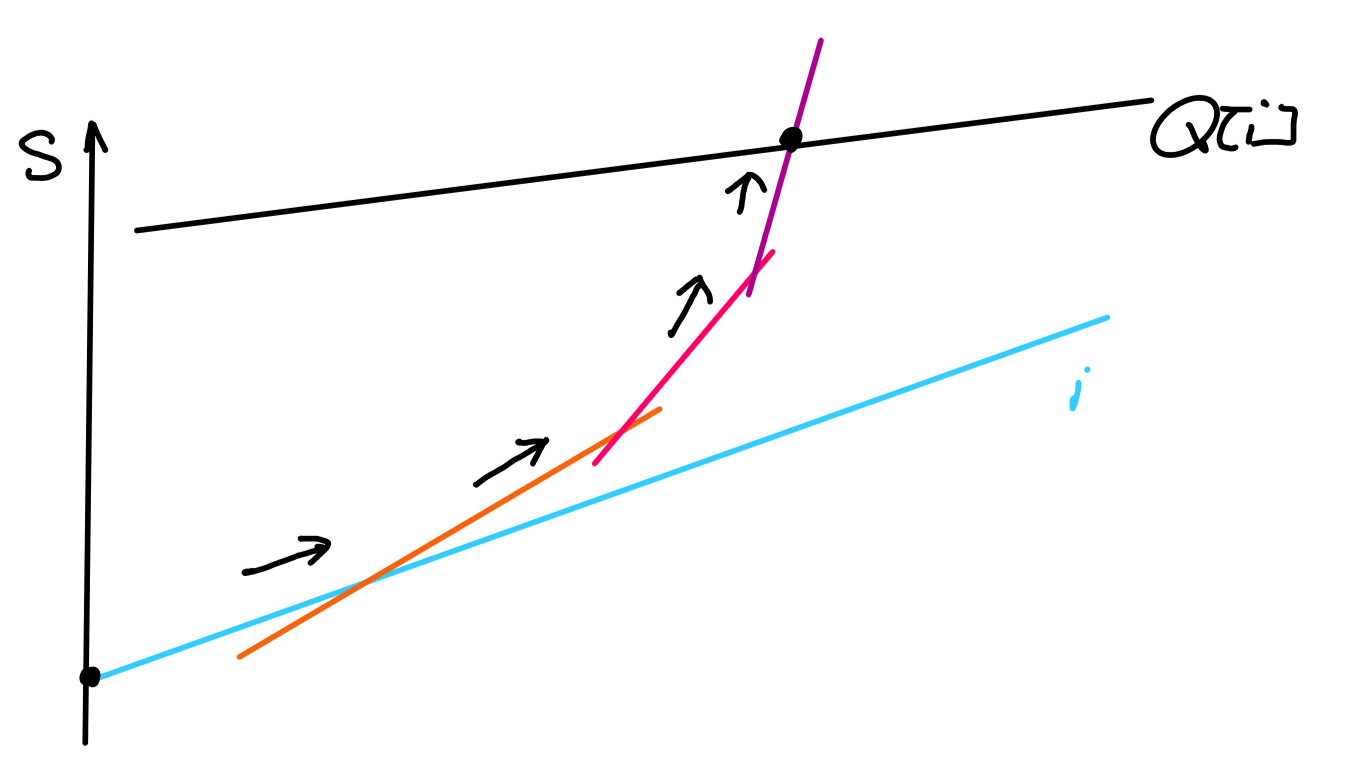
这是因为,假设存在一种更优方案,那么它一定与我们的原方案在某点处相交,从而这与我们最优方案的构造不符。假设不成立。
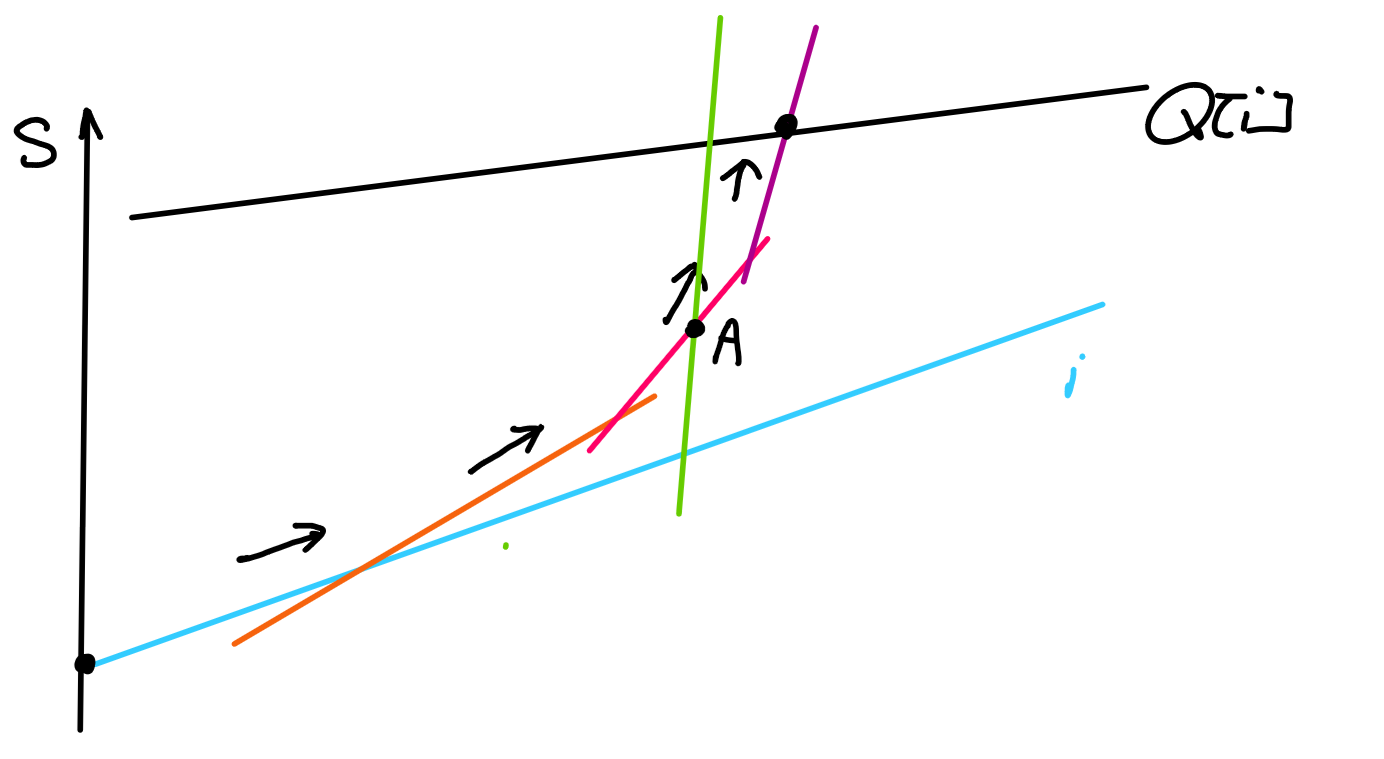
- 如图,绿线表示假设存在的更优方案,那么在A点我们遇到了向上拐点却没有拐。
性质2:设up_fa[i]表示射线i出发后碰到的第一个向上拐点对应的直线(如果三线共点,那么选择该点处斜率最大的线)

- 如图,up_fa[i]=j
那么,性质1中描述的方案,就是不断从当前射线i转入up_fa[i]而成的。
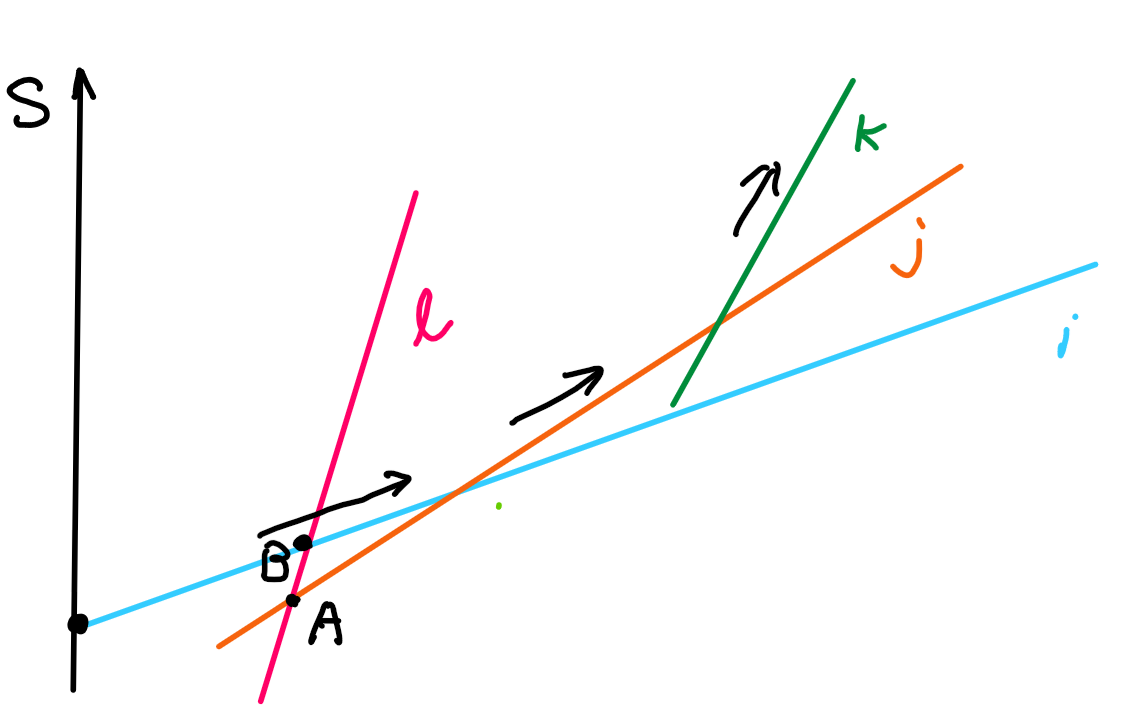
这个性质也是比较显然的。假设性质1中的方案是图中的黑色箭头i->j->k,假设up_fa[j]不是k而是l,那么由于有l>j>i以及l和j均通过i下方的A点,所以l与i的交点B一定在i与j的交点之前。所以从i出发应在B点转入l,而不是继续走黑色路线,这与我们在性质1中规定的规则不符。
更一般地、如果按照性质1规定的方案走出的路线是\(i_1,i_2,…,i_t\),那么一旦任何一个\(i_s(2{\leq}s<t)\)使得up_fa[\(i_s\)]\({\neq}\)\(i_{s+1}\),那么\(i_{s-1}\)就一定在遇到\(i_s\)之前遇到up_fa[\(i_s\)],从而与我们在性质1中规定的规则不符。
有了性质1、2,我们就可以通过对所有i计算up_fa[i],然后通过树上倍增求解。下面讲一下计算up_fa[i]的方法。
up_fa[i],是所有\(A[j]>A[i]\)且\(j>i\)的j中,使得射线\(i,j\)交点横坐标最小的那个。射线\(i,j\)交点的横坐标t是:
所以,如果我们把所有射线i,按坐标\((i,A[i])\)对应另一个平面中的一个点,所求的就是点i右上方、与i连线斜率最小的点j。(若点i右上方没有点,说明原来的射线i与其他射线不相交,可以置up_fa[i]=0)
性质3:如果点x在点y的左上方,那么y下方的所有点的up_fa均不为x。
性质4:如果x,y,z纵坐标依次减小,且\(k(y,z)>k(x,y)>0\),(如下图)那么z下方的所有点的up_fa均不为y。
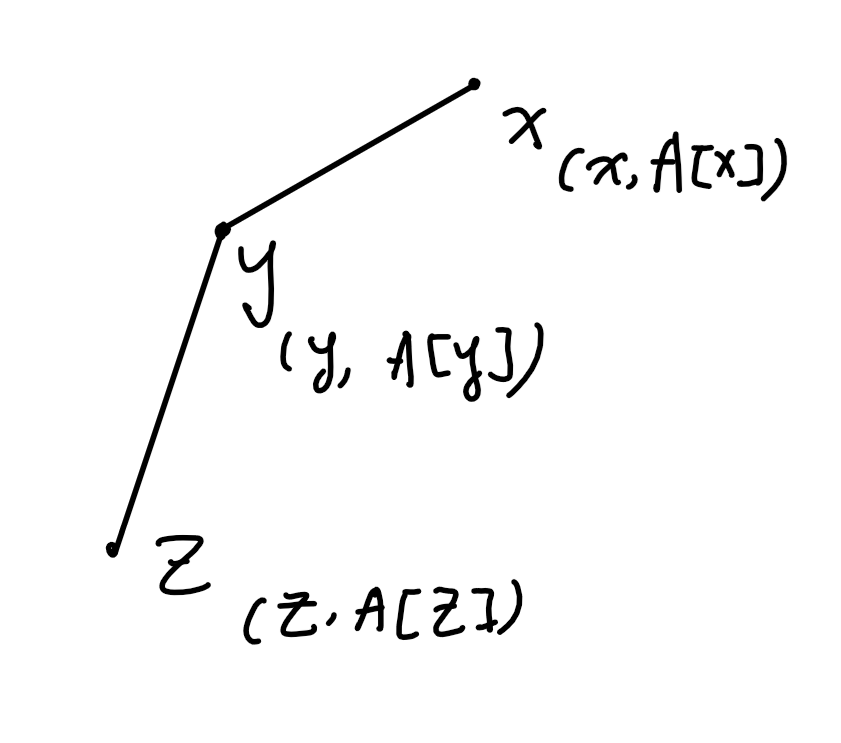
这两条性质显然。由此,我们可以把所有点按纵坐标从大到小排序,然后维护一个下凸包,轮到点i的时候,按性质3、4依次从下到上删去凸包上的点,直到不能删,此时凸包最下方的点就是up_fa[i]。然后把i加进凸包。
至此,\(A[i]>A[Q[i]]\)的情况考虑完毕,时间复杂度是计算up_fa[]的O(n)加上树上倍增的O(nlogn)。
对于\(A[i]<A[Q[i]]\),做法类似,只需要先计算出第一个向下拐点对应的射线down_fa[],过程中利用凸包维护,再利用树上倍增,同样可以求解。
总时间复杂度\(O(nlogn)\)。
代码
#include<bits/stdc++.h>
using namespace std;
#define N 200000
#define rg register
#define ll long long
#define eps 1e-8
inline ll read(){
ll s = 0,ww = 1;
char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-')ww = -1;ch = getchar();}
while('0' <= ch && ch <= '9'){s = 10 * s + ch - '0';ch = getchar();}
return s * ww;
}
inline void write(ll x){
if(x < 0)x = -x,putchar('-');
if(x > 9)write(x / 10);
putchar('0' + x % 10);
}
ll p[N+5],A[N+5],Q[N+5],up_fa[N+5][20],down_fa[N+5][20];
inline double k(ll j,ll i){
return 1.0 *(A[j] - A[i]) / (j - i);
}
inline bool cmp1(ll x,ll y){
return A[x] < A[y];
}
ll q[N+5];
ll n;
inline void calcfa(){
ll L,R;
q[L=R=1] = 0;
for(rg ll i = n;i >= 1;i--){
ll u = p[i];
while((L<R && k(q[R],u)<0) || (L+1<R && k(q[R],u)>k(q[R-1],q[R])))R--;
q[++R] = u;
up_fa[u][0] = q[R-1];
}
for(rg ll j = 1;j <= 18;j++)
for(rg ll i = 1;i <= n;i++)up_fa[i][j] = up_fa[up_fa[i][j-1]][j-1];
q[L=R=1] = 0;
for(rg ll i = 1;i <= n;i++){
ll u = p[i];
while((L<R && k(q[R],u)<0) || (L+1<R && k(q[R],u)>k(q[R-1],q[R])))R--;
q[++R] = u;
down_fa[u][0] = q[R-1];
}
for(rg ll j = 1;j <= 18;j++)
for(rg ll i = 1;i <= n;i++)down_fa[i][j] = down_fa[down_fa[i][j-1]][j-1];
}
inline bool up_check(ll u,ll l){ //当前射线u遇到的第一个向下拐点是否在目标线l以上
if(down_fa[u][0] == 0)return 0;
double x = k(u,down_fa[u][0]),y = (double)u * x - (double)A[u];
return (double)l * x - y - (double)A[l] < -eps;
}
inline bool down_check(ll u,ll l){ //当前射线u遇到的第一个向上拐点是否在目标线l以下
if(up_fa[u][0] == 0)return 0;
double x = k(u,up_fa[u][0]),y = (double)u * x - (double)A[u];
return (double)l * x - y - (double)A[l] > eps;
}
inline ll gcd(ll a,ll b){
return b ? gcd(b,a % b) : a;
}
inline void print(ll u,ll v){
ll x = A[u] - A[v],y = u - v;
ll d = gcd(x,y);
x /= d,y /= d;
write(x),putchar('/'),write(y),putchar('\n');
}
int main(){
n = read();
for(rg ll i = 1;i <= n;i++)A[i] = read();
for(rg ll i = 1;i <= n;i++)Q[i] = read();
for(rg ll i = 1;i <= n;i++)p[i] = i;
sort(p+1,p+n+1,cmp1);
calcfa();
for(rg ll i = 1;i <= n;i++){
if(A[Q[i]] < A[i]){
ll u = i;
if(down_check(i,Q[i])){ //需要传送多于1次
for(rg ll j = 18;j >= 0;j--)if(down_check(up_fa[u][j],Q[i]))u = up_fa[u][j];
u = up_fa[u][0];
if(u < Q[i])puts("-1");
else print(u,Q[i]);
}
else if(i < Q[i])puts("-1");
else print(i,Q[i]);
}
else{
ll u = i;
if(up_check(i,Q[i])){ //需要传送多于1次
for(rg ll j = 18;j >= 0;j--)if(up_check(down_fa[u][j],Q[i]))u = down_fa[u][j];
u = down_fa[u][0];
if(u > Q[i])puts("-1");
else print(u,Q[i]);
}
else if(i > Q[i])puts("-1");
else print(i,Q[i]);
}
}
return 0;
}

