LeetCode 二叉树的层序遍历算法题解 All In One

LeetCode 二叉树的层序遍历算法题解 All In One

js / ts 实现二叉树的层序遍历

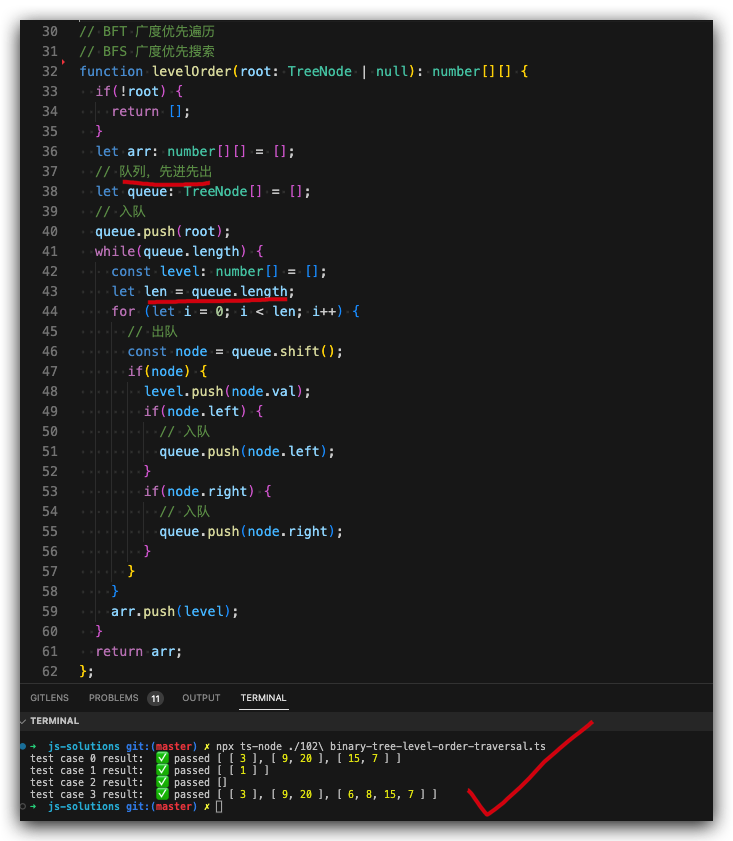
BFT 广度优先遍历 => Tree/树 ✅

BFS 广度优先搜索 => Graph/图

二叉树的层序遍历 原理 & 图解

// queue 队列，先进先出
let queue: TreeNode[] = [];

LeetCode 102. Binary Tree Level Order Traversal

LeetCode 102. 二叉树的层序遍历

"use strict";

/**
 *
 * @author xgqfrms
 * @license MIT
 * @copyright xgqfrms
 * @created 2023-02-19
 * @modified
 *
 * @description 102. Binary Tree Level Order Traversal
 * @description 102. 二叉树的层序遍历
 * @difficulty Medium
 * @ime_complexity O(n)
 * @space_complexity O(n)
 * @augments
 * @example
 * @link https://leetcode.com/problems/binary-tree-level-order-traversal/
 * @link https://leetcode.cn/problems/binary-tree-level-order-traversal/
 * @solutions
 *
 * @best_solutions
 *
 */

export {};

const log = console.log;

// BFT 广度优先遍历
// BFS 广度优先搜索

function levelOrder(root: TreeNode | null): number[][] {
  if(!root) {
    return [];
  }
  let arr: number[][] = [];
  // 队列，先进先出
  let queue: TreeNode[] = [];
  // 入队
  queue.push(root);
  while(queue.length) {
    const level: number[] = [];
    let len = queue.length;
    for (let i = 0; i < len; i++) {
      // 出队
      const node = queue.shift();
      if(node) {
        level.push(node.val);
        if(node.left) {
          // 入队
          queue.push(node.left);
        }
        if(node.right) {
          // 入队
          queue.push(node.right);
        }
      }
    }
    arr.push(level);
  }
  return arr;
};

class TreeNode {
  val: number;
  left: TreeNode | null;
  right: TreeNode | null;
  constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
  }
}

// LeetCode tree test case
// 二叉树生成原理：递归依次遍历（左=>右），遇到 null 返回 (✅ null 后面不能有子节点了)
const BinaryTreeGenerator = (arr:any[] = [], i = 0): (TreeNode | null) => {
  if(arr.length === 0 || i > arr.length - 1 || arr[i] === null) {
    return null;
  }
  const node = new TreeNode(arr[i]);
  // 先左后右， 依次遍历
  node.left = BinaryTreeGenerator(arr, 2 * i + 1);
  node.right = BinaryTreeGenerator(arr, 2 * i + 2);
  return node;
}

// 测试用例 test cases
const testCases = [
  {
    input: [3,9,20,null,null,15,7],
    result: [[3],[9,20],[15,7]],
    desc: 'value equal to [[3],[9,20],[15,7]]',
  },
  {
    input: [1],
    result: [[1]],
    desc: 'value equal to [[1]]',
  },
  {
    input: [],
    result: [],
    desc: 'value equal to []',
  },
  {
    input: [3,9,20,6,8,15,7],
    result: [[3],[9,20],[6,8,15,7]],
    desc: 'value equal to [[3],[9,20],[6,8,15,7]]',
  },
];

for (const [i, testCase] of testCases.entries()) {
  const tree = BinaryTreeGenerator(testCase.input);
  const result = levelOrder(tree);
  log(`test case ${i} result: `, JSON.stringify(result) === JSON.stringify(testCase.result) ? `✅ passed` : `❌ failed`, result);
}



// $ npx ts-node ./102\ binary-tree-level-order-traversal.ts

/*

test case 0 result:  ✅ passed [ [ 3 ], [ 9, 20 ], [ 15, 7 ] ]
test case 1 result:  ✅ passed [ [ 1 ] ]
test case 2 result:  ✅ passed []
test case 3 result:  ✅ passed [ [ 3 ], [ 9, 20 ], [ 6, 8, 15, 7 ] ]

*/

(🐞 反爬虫测试！打击盗版⚠️）如果你看到这个信息, 说明这是一篇剽窃的文章，请访问 https://www.cnblogs.com/xgqfrms/ 查看原创文章！

BFS 解题思路

本文将会讲解为什么这道题适合用广度优先搜索（BFS），以及 BFS 适用于什么样的场景。

DFS（深度优先搜索）和 BFS（广度优先搜索）就像孪生兄弟，提到一个总是想起另一个。然而在实际使用中，我们用 DFS 的时候远远多于 BFS。那么，是不是 BFS 就没有什么用呢？

如果我们使用 DFS/BFS 只是为了遍历一棵树、一张图上的所有结点的话，那么 DFS 和 BFS 的能力没什么差别，我们当然更倾向于更方便写、空间复杂度更低的 DFS 遍历。不过，某些使用场景是 DFS 做不到的，只能使用 BFS 遍历。这就是本文要介绍的两个场景：「层序遍历」、「最短路径」。

本文包括以下内容：

DFS 与 BFS 的特点比较
BFS 的适用场景
如何用 BFS 进行层序遍历
如何用 BFS 求解最短路径问题

https://leetcode.cn/problems/binary-tree-level-order-traversal/solution/bfs-de-shi-yong-chang-jing-zong-jie-ceng-xu-bian-l/

refs

---

---

©xgqfrms 2012-2021

www.cnblogs.com/xgqfrms 发布文章使用：只允许注册用户才可以访问！

原创文章，版权所有©️xgqfrms, 禁止转载 🈲️，侵权必究⚠️！

---