js 代码性能优化原理剖析与实战 All In One

fibonacci 性能优化

tail-call optimization / 尾调用优化

函数式编程，请注意 JavaScript 中递归的性能影响; 对于深度递归，请考虑使用迭代来避免堆栈溢出;

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Language_Overview

http://wiki.c2.com/?TailCallOptimization

https://webkit.org/blog/6240/ecmascript-6-proper-tail-calls-in-webkit/

In computer science, a tail call is a subroutine call performed as the final action of a procedure.
If the target of a tail is the same subroutine, the subroutine is said to be tail recursive, which is a special case of direct recursion.
Tail recursion (or tail-end recursion) is particularly useful, and is often easy to optimize in implementations.

在计算机科学中，尾调用是作为过程的最终操作执行的子例程调用。
如果尾的目标是同一个子程序，则称该子程序是尾递归的，这是直接递归的一种特殊情况。
尾递归（或尾端递归）特别有用，并且在实现中通常很容易优化。

https://en.wikipedia.org/wiki/Tail_call

https://zh.wikipedia.org/wiki/尾调用

性能优化

recursion / 递归 ❌ 简单好理解，但是性能不好

https://developer.mozilla.org/en-US/docs/Glossary/Recursion

memory cached / 内存缓存 ✅

iteration / 迭代替换递归 🚀

~~https://developer.mozilla.org/en-US/docs/Glossary/Iteration~~

https://developer.mozilla.org/en-US/search?q=Iteration

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Guide/Iterators_and_Generators

https://developer.mozilla.org/en-US/docs/Web/API/KeyframeEffect/iterationComposite

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Iteration_protocols

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Guide/Loops_and_iteration

https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Global_Objects/Function/caller

tail-call optimization / 尾调用优化 🚀

Hardware Acceleration / 硬件加速 ❓

WebAssembly / WebGL / Web API (requestAnimationFrame / cancelAnimationFrame ...)

https://developer.mozilla.org/en-US/docs/Web/Performance/Animation_performance_and_frame_rate

https://developer.mozilla.org/en-US/docs/Web/API/window/requestAnimationFrame
https://developer.mozilla.org/en-US/docs/Web/API/Window/cancelAnimationFrame

demos

fibonacci / 斐波那契



testCase fib(0) = 0
testCase fib(1) = 1
testCase fib(2) = 1
testCase fib(3) = 2
testCase fib(4) = 3
testCase fib(5) = 5
testCase fib(6) = 8
testCase fib(7) = 13
testCase fib(8) = 21
testCase fib(9) = 34
testCase fib(10) = 55
testCase fib(11) = 89
testCase fib(12) = 144
testCase fib(13) = 233
testCase fib(14) = 377
testCase fib(15) = 610
testCase fib(16) = 987
testCase fib(17) = 1597
testCase fib(18) = 2584
testCase fib(19) = 4181
testCase fib(20) = 6765
testCase fib(21) = 10946
testCase fib(22) = 17711
testCase fib(23) = 28657
testCase fib(24) = 46368
testCase fib(25) = 75025
testCase fib(26) = 121393
testCase fib(27) = 196418
testCase fib(28) = 317811
testCase fib(29) = 514229
testCase fib(30) = 832040
testCase fib(31) = 1346269
testCase fib(32) = 2178309
testCase fib(33) = 3524578
testCase fib(34) = 5702887
testCase fib(35) = 9227465
testCase fib(36) = 14930352
testCase fib(37) = 24157817
testCase fib(38) = 39088169
testCase fib(39) = 63245986
testCase fib(40) = 102334155
testCase fib(41) = 165580141
testCase fib(42) = 267914296
testCase fib(43) = 433494437
testCase fib(44) = 701408733
testCase fib(45) = 1134903170
testCase fib(46) = 1836311903
testCase fib(47) = 2971215073
testCase fib(48) = 4807526976
testCase fib(49) = 7778742049
testCase fib(50) = 12586269025

recursion / 递归

// n      0 1 2 3 4 5 6 ... n
// fib(n) 0 1 1 2 3 5 8 ... n

// 1. 递归
function fib(n) {
  if(n < 2) {
    return n;
  }
  return fib(n - 1) + fib(n - 2);
}

function autoTest(fn, n) {
  const testCases = [...new Uint8Array(n + 1)].map((item, i) => i);
  console.clear();
  const start = performance.now();
  for (const testCase of testCases) {
    console.log(`testCase fib(${testCase}) =`, fn(testCase));
  }
  const end = performance.now();
  console.log(`total time used: ${(end - start) / 1000}s`);
}

// n <= 30
// n <= 60
// n <= 100
autoTest(fib, 50);

fib(49)
total time used: 306.43480000001193s ❌

fib(50)
total time used: 547.9031000000239s ❌

iteration / 迭代

// n      0 1 2 3 4 5 6 ... n
// fib(n) 0 1 1 2 3 5 8 ... n

// 2. 迭代
function fib(n) {
  if(n < 2) {
    return n;
  }
  let n1 = 0;
  let n2 = 1;
  while(n >= 2) {
    // swap
    [n2, n1] = [n1 + n2, n2];
    n--;
  }
  return n2;
}

function autoTest(fn, n) {
  const testCases = [...new Uint8Array(n + 1)].map((item, i) => i);
  console.clear();
  const start = performance.now();
  for (const testCase of testCases) {
    console.log(`testCase fib(${testCase}) =`, fn(testCase));
  }
  const end = performance.now();
  console.log(`total time used: ${(end - start) / 1000}s`);
}

// n <= 30
// n <= 60
// n <= 100
autoTest(fib, 50);

total time used: 0.002100000023841858s

memory cached

// n      0 1 2 3 4 5 6 ... n
// fib(n) 0 1 1 2 3 5 8 ... n

// 3. 内存缓存
function fib(n, cache) {
  cache = cache ?? {};
  if(n < 2) {
    return n;
  }
  if(!cache[n]) {
    cache[n] = fib(n - 1, cache) + fib(n - 2, cache);
  }
  return cache[n];
}

function autoTest(fn, n) {
  const testCases = [...new Uint8Array(n + 1)].map((item, i) => i);
  console.clear();
  const start = performance.now();
  for (const testCase of testCases) {
    console.log(`testCase fib(${testCase}) =`, fn(testCase));
  }
  const end = performance.now();
  console.log(`total time used: ${(end - start) / 1000}s`)
}

// n <= 30
// n <= 60
// n <= 100
autoTest(fib, 50);

total time used: 0.001899999976158142s

tail-call optimization

// n      0 1 2 3 4 5 6 ... n
// fib(n) 0 1 1 2 3 5 8 ... n

// IIFE
(() =>  {
"use strict";

// 4. 尾调用优化
function fib(n, pre = 0, cur = 1) {
  if (n === 0) {
    return pre;
    // return n;
  }
  if (n === 1) {
    return cur;
  }
  return fib(n - 1, cur, pre + cur);
}

function autoTest(fn, n) {
  const testCases = [...new Uint8Array(n + 1)].map((item, i) => i);
  console.clear();
  const start = performance.now();
  for (const testCase of testCases) {
    console.log(`testCase fib(${testCase}) =`, fn(testCase));
  }
  const end = performance.now();
  console.log(`total time used: ${(end - start) / 1000}s`)
}

// n <= 30
// n <= 60
// n <= 100
autoTest(fib, 50);

})();

total time used: 0.001699999988079071s

// IIFE
(() => {
  "use strict";
  // 4. 尾调用优化
  function fib(n, pre = 0, cur = 1) {
    if (n === 0) {
      return pre;
      // return n;
    }
    if (n === 1) {
      return cur;
    }
    return fib(n - 1, cur, pre + cur);
  }
  // function fib(n, pre = 0, cur = 1) {
  //   // ??? pre， cur 没有缓存 ❌
  //   if (n === 0) {
  //     return 0;
  //   }
  //   if (n === 1) {
  //     return 1;
  //   }
  //   return fib(n - 1, cur, pre + cur);
  // }
  // function fib(n, pre = 0, cur = 1) {
  //   // ??? n 没有缓存 ❌
  //   if(n < 2) {
  //     return n;
  //   }
  //   return fib(n - 1, cur, pre + cur);
  // }
  // function fib(n, pre = 0, cur = 1) {
  //   if(n < 2) {
  //     return n;
  //   }
  //   // swap
  //   [pre, cur] = [cur, cur + pre];
  //   return fib(n - 1, pre, cur);
  // }
  function autoTest(fn, n) {
    const testCases = [...new Uint8Array(n + 1)].map((item, i) => i);
    console.clear();
    const start = performance.now();
    for (const testCase of testCases) {
      console.log(`testCase fib(${testCase}) =`, fn(testCase));
    }
    const end = performance.now();
    console.log(`total time used: ${(end - start) / 1000}s`)
  }
  autoTest(fib, 50);
})();

total time used: 0.001599999964237213s 🚀

没有缓存 bug ??? stackoverflow ???

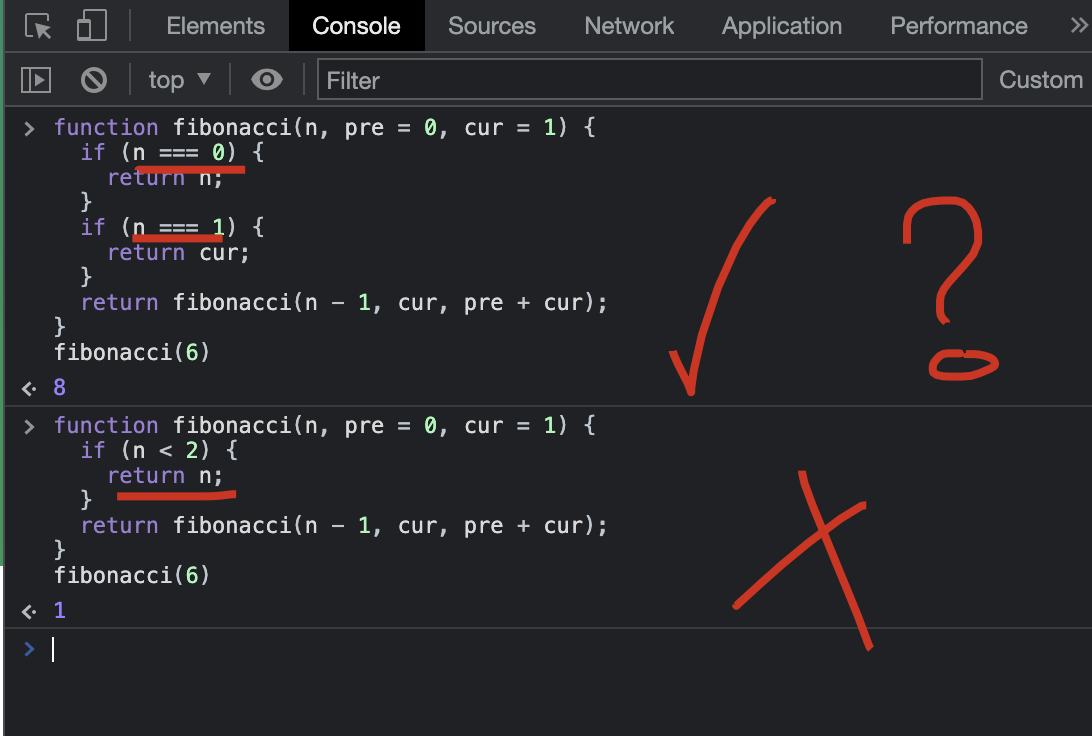
function fibonacci(n, pre = 0, cur = 1) {
  // ✅ 
  if (n === 0) {
    return n;
  }
  // ✅ 
  if (n === 1) {
    return cur;
  }
  return fibonacci(n - 1, cur, pre + cur);
}
fibonacci(6)
// 8  ✅

function fibonacci(n, pre = 0, cur = 1) {
  // n 没有缓存 ❌
  if (n < 2) {
    return n;
  }
  return fibonacci(n - 1, cur, pre + cur);
}
fibonacci(6)
// 1 ❌

js tail-call-optimization fibonacci

ES6

(function(){
    function fib(n, sum=0, prev=1) {
      if (n <= 1) return sum;
      return fib(n-1, prev+sum, sum);
    }
})();

https://medium.com/hackernoon/es6-tail-call-optimization-43f545d2f68b

// After modification
'use strict'
function fibonacci(n, pre, cur) {
  if (n === 0) {
    return n;
  }
  if (n === 1) {
    return cur;
  }
  return fibonacci(n - 1, cur, pre + cur);
}
// call
fibonacci(6, 0, 1)

'use strict'
function fibonacci(n, pre = 0, cur = 1) {
  if (n === 0) {
    return n;
  }
  if (n === 1) {
    return cur;
  }
  return fibonacci(n - 1, cur, pre + cur);
}
fibonacci(6)

https://programmer.group/optimize-fibonacci-function-with-tail-recursion.html

ES5

function fib(n) {
  return function(n,a,b) {
    return n>0 ? arguments.callee(n-1, b, a+b) : a;
  } (n,0,1);
}

function fib(n) {
    function recur(n, a, b) {
        if (n > 0) {
            return recur(n - 1, b, a + b);
        } else {
            return a;
        }
    }
    return recur(n, 0, 1);
}

https://stackoverflow.com/questions/6877213/tail-recursion-and-fibonacci

https://rosettacode.org/wiki/Fibonacci_sequence#JavaScript

严格模式 `"use strict";`

ES6 尾调用优化只在严格模式下开启，正常模式是无效的。

这是因为在正常模式下，函数内部有两个变量，可以跟踪函数的调用栈。

arguments：返回调用时函数的参数。

func.caller：返回调用当前函数的那个调用者函数。

尾调用优化发生时，函数的调用栈会改写，因此上面两个变量就会失真。
严格模式禁用这两个变量，所以尾调用模式仅在严格模式下生效。

factorial / 阶乘

https://www.shuxuele.com/numbers/factorial.html

// 阶乘函数（符号：!）的意思是把逐一减小的自然数序列相乘
function factorial(n) {
  if(n === 1) {
    return 1;
  }
  return n * factorial(n - 1);
};

// 尾调用优化 / 尾递归优化
function factorial(n, multi = 1) {
  if(n === 1) {
    return multi;
  }
  multi = n * multi;
  return factorial(n - 1, multi);
};

阶乘, 科学计数法 e bug ❌

(() => {
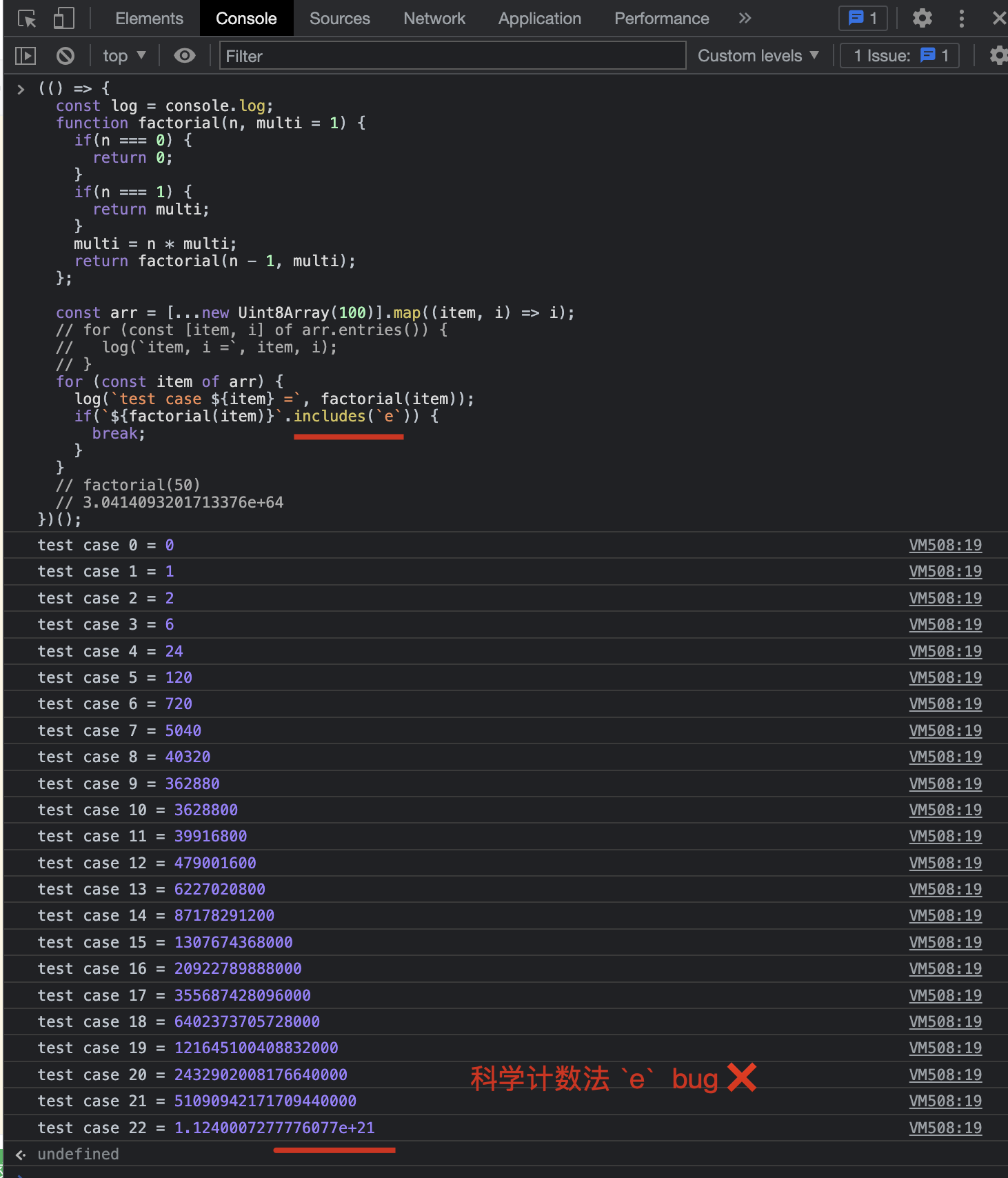
  const log = console.log;
  function factorial(n, multi = 1) {
    if(n === 0) {
      return 0;
    }
    if(n === 1) {
      return multi;
    }
    multi = n * multi;
    return factorial(n - 1, multi);
  };

  const arr = [...new Uint8Array(100)].map((item, i) => i);
  // for (const [item, i] of arr.entries()) {
  //   log(`item, i =`, item, i);
  // }
  for (const item of arr) {
    log(`test case ${item} =`, factorial(item));
    if(`${factorial(item)}`.includes(`e`)) {
      break;
    }
  }
  // factorial(50)
  // 3.0414093201713376e+64
})();

(() => {
  const log = console.log;
  function factorial(n, multi = 1) {
    if(n === 0) {
      return 0;
    }
    if(n === 1) {
      return multi;
    }
    multi = n * multi;
    return factorial(n - 1, multi);
  };

  const arr = [...new Uint8Array(100)].map((item, i) => i);
  // for (const [item, i] of arr.entries()) {
  //   log(`item, i =`, item, i);
  // }
  for (const item of arr) {
    log(`testCase factorial(${item}) =`, factorial(item));
    if(`${factorial(item)}`.includes(`e`)) {
      break;
    }
  }
  // factorial(50)
  // 3.0414093201713376e+64
  // 阶乘, `科学计数法` `e` bug ❌
})();

https://leetcode.cn/problems/factorial-trailing-zeroes/

https://leetcode.com/problems/factorial-trailing-zeroes/