LeetCode & Binary Search 解题模版

LeetCode & Binary Search 解题模版

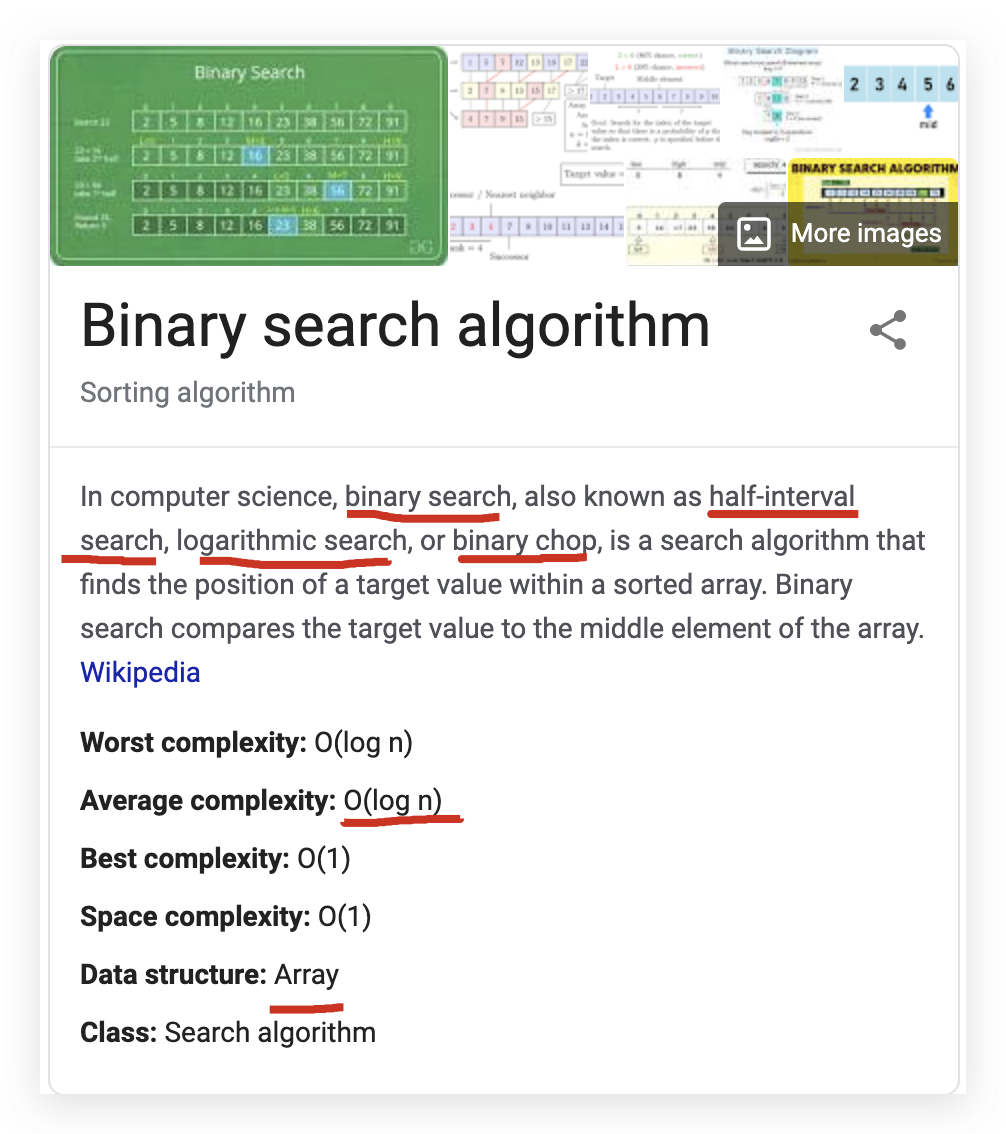
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array.

在计算机科学中，二分搜索（也称为半间隔搜索，对数搜索或二进制印章）是一种搜索算法，用于查找排序数组中目标值的位置。

Big O

Worst complexity: O(log n)
Average complexity: O(log n)
Best complexity: O(1)
Space complexity: O(1)
Data structure: Array
Class: Search algorithm

solutions

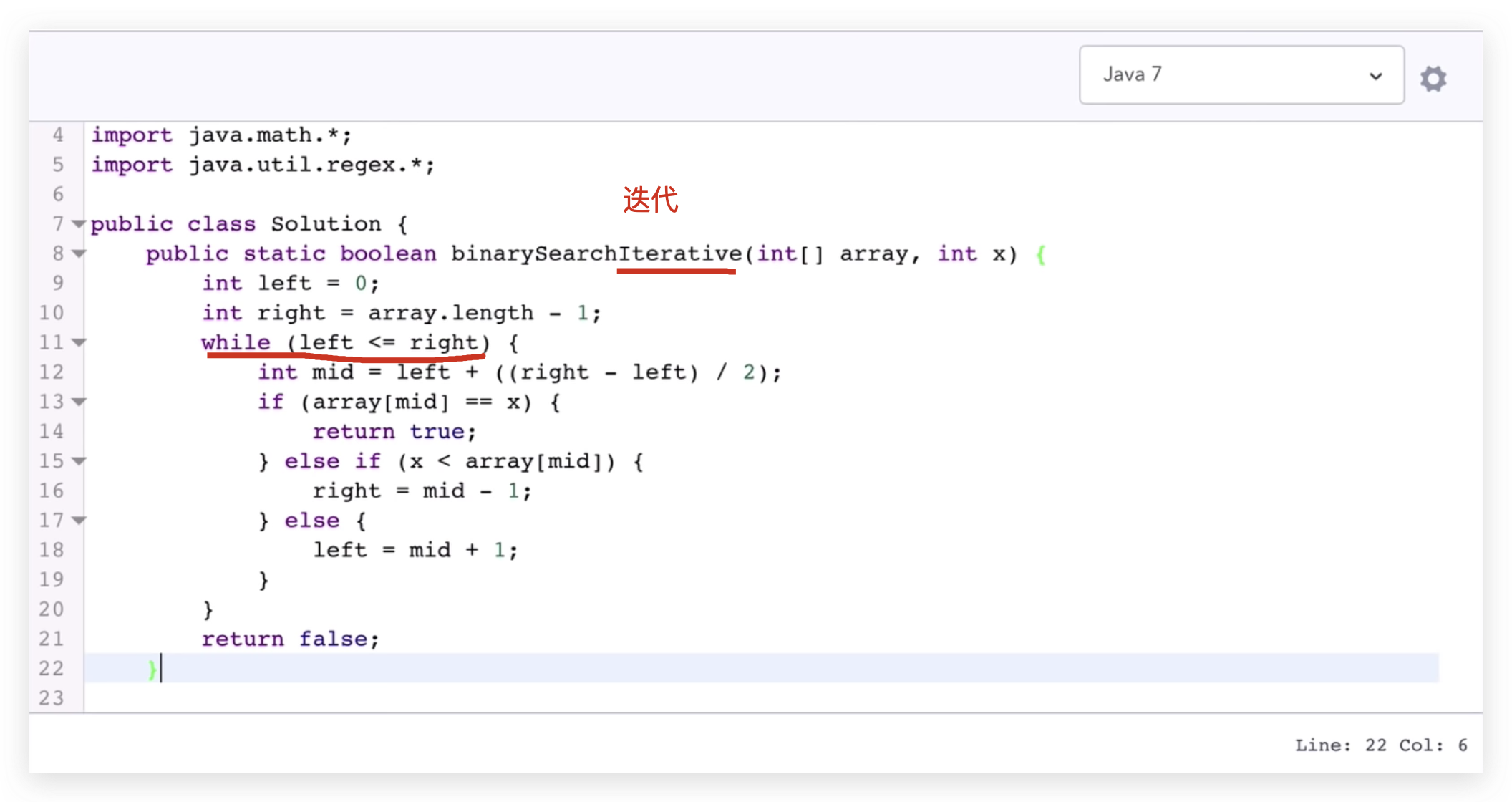
1. 递归

2. 迭代

leeetcode & binary-search

https://leetcode.com/problems/binary-search/

"use strict";

/**
 *
 * @author xgqfrms
 * @license MIT
 * @copyright xgqfrms
 * @created 2020-07-30
 * @modified
 *
 * @description 704. Binary Search
 * @difficulty Easy
 * @complexity O(n)
 * @augments
 * @example
 * @link https://leetcode.com/problems/binary-search/
 * @solutions
 *
 */

const log = console.log;

/*

Example 1:

Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4

Example 2:

Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1

*/


/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
  let left = 0;
  let right = nums.length - 1;
  while (left <= right) {
    // left + 差值
    let mid = left + Math.floor((right - left) / 2);
    // log(`mid`, nums[mid])
    if(nums[mid] === target) {
      // nums[mid] 值
      return nums.indexOf(nums[mid]);
      // return true;
    } else if(nums[mid] > target) {
      right = mid - 1;
    } else {
      left = mid + 1;
    }
  }
  return -1;
  // return false;
};


const test = search([-1,0,3,5,9,12], 9);
const test1 = search([-1,0,3,5,9,12], 2);

log(test)
log(test1)
// 4
// -1

best solution

https://leetcode.com/submissions/detail/374279676/

runtime

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
    if(!nums.length) return -1
    let start = 0, end = nums.length - 1
    while(start <= end) {
        if(nums[start] === target) return start
        if(nums[end] === target) return end
        let mid = Math.floor(start + (end - start) / 2)
        if(nums[mid] === target) return mid
        if(target > nums[mid]) {
            start = mid + 1
        } else {
            end = mid - 1
        }
    }
    return -1
};

Memory

/**
 * @param {number[]} nums
 * @param {number} target
 * @return {number}
 */
var search = function(nums, target) {
  let low = 0;
  let high = nums.length -1;
  while (low <= high) {
    const mid = parseInt((low + high) / 2);
    if (nums[mid] === target) {
      return mid;
    }
    if (nums[mid] < target) {
      low = mid + 1;
    }
    if (nums[mid] > target) {
      high = mid - 1;
    }
  }
  return -1;
}

refs

https://en.wikipedia.org/wiki/Binary_search_algorithm

https://www.youtube.com/results?search_query=binary+search+algorithm

https://www.youtube.com/watch?v=P3YID7liBug

---

---

©xgqfrms 2012-2020

www.cnblogs.com 发布文章使用：只允许注册用户才可以访问！

---