机器学习算法-logistic回归算法

Logistic回归算法调试

一、算法原理

   Logistic回归算法是一种优化算法，主要用用于只有两种标签的分类问题。其原理为对一些数据点用一条直线去拟合，对数据集进行划分。从广义上来讲这也是一种多元线性回归方法，所不同的是这种算法需要找出的是能够最大可能地将两个类别划分开来而不是根据直线关系预测因变量的值。Logistic回归算法的核心部分是sigmoid函数：

其中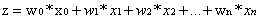，x_i为数据集的第i个特征。定义损失函数损失函数：

损失函数越小表明曲线拟合的效果就越好。利用梯度向上法更新x的系数W，求出W的最优解。梯度向上法的原理就是要求得一个函数的极值最好的方法就是沿着该函数的梯度方向进行，梯度可用偏导数求解。Logistic回归算法的损失函数的梯度grad为 。

通过不断的更新x的权重迭代一定次数之后就能够得到想要的w。

二、算法调试

2.1梯度下降法算法

　　首先定义导入数据的函数loadDataSet（），使得数据的导入更加方便。为运行方便，对书中的代码稍作改变，有输入文件位置改成直接输入矩阵。梯度下降算法中的下面两行来自于对损失函数的求解，推到过程并不复杂。

运行loadDataSet对输入的算法进行测试，能够正常运行结果如下：

2.2  画出决策边界

   在测试完梯度上升算法可行之后，实际上解出了一组回归系数。为了更好的理解logistic算法，需要把分隔线画出来。定义函数plotBestFit，在pycharm中输入代码。在这个程序中值得注意的是其中使用的getA这个函数，这是numpy库中的maxtri模块中的一个函数，作用刚好与mat相反，是把矩阵转化成数组。如果去掉之后则不能正常运行，主要原因是矩阵的每一行长度只能为1，不能像数组一样。通过测试之后的结果如图1.

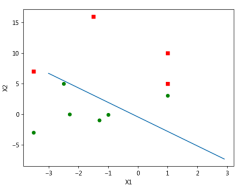
          图1

2.3随机梯度上升算法

　　由于构造梯度上升算法时每次都要便历整个数据集，当数据量非常庞大时，运算量非常大。下面是梯段上升算法的一种改进算法，随机梯度上升算法。其原理是每一次只用一个样本更新回归系数，当新的样本输入时再进行增量式更新。定义stocGradAscent0函数，期待与梯度上升算法非常相似。输入代码进行验证，发现之间验证会出现以下错误：

出现这种问题是因为“*”这个运算符号的问题，在列表之间的计算时，只能够用整数去乘另外一个列表，这可能是因为在python中一个数字乘一个矩阵时会先把数字复制成为一个长度与被乘列表相同的列表，然后再相乘。但是其中的问题在于生成复制列表时只能对整数起作用，因而出现上述问题。修改的方法是将列表转化为矩阵，然后在再运算。修改的地方为：

 

 

经过调试能够很好的输出结果，如图2所示：

                                      图2                                

从结果来看划分的效果并不如之前的好，这是因为有些系数的收敛速度非常慢，经过500次迭代并不能达到稳定值，因此需要进行下一步改进。

2.4 改进的随机梯度上升法

   为了避免系数在迭代过程中来回波动，从而收敛到某个值。对随机上升梯度法进行了改进，一方面对α进行调整，这回使得波动减小；另一方面采用随机选择样本来更新回归系数，这将会减少周期性波动。然后调试程序，输入代码运行并未发现问题，能够直接运行出结果，如图3所示：

   　　　　　　　　　　  图3                               

从图中可以看出分类的效果非常好，把数据集完全分类开来，证明了算法的有效性。

2.5 logistic回归分类算法

   Logistic优化算法已经找出来了，下面需要用logistic回归进行分类测试。首先构造logistic分类器。由于选取的为西瓜数据集，与教材中的数据有所不用，因此代码稍有不同。但方法是一样的。主要程序代码如下：

def classifyVector(inX,weights):
    prob=sigmoid(sum(inX*weights))
    if prob>0.5:return 1.0
    else: return 0.0

def colicTest(testSet,weights,labelset):#输入测试集，回归系数，标签
    errorcount = 0
    n = shape(testSet)[0]
    for i in range(n):
        if classifyVector(array(testSet[i]),weights) != labelset[i]:
            errorcount = errorcount + 1
    errorrate = errorcount*1.0/n
    return errorrate

def multiTest(testSet,weights,labelSet):
    numTests=10;errorSum=0.0
    for k in range(numTests):
        errorSum=errorSum+colicTest(testSet,weights,labelSet)
    print('平均错误率为%s'%(errorSum/numTests))

　　这里我们采用的是西瓜数据集，由于样本较少预测效果不太好，使用三种算法之后，错误率在55%左右。如果把数据集即作为训练集又作为测试集准确率在75%左右，通过修改迭代次数最终准确率会收敛到84%。

三、总结

     首先通过算法的调试，对算法的原理及实现方法有了进一步的理解。从理论上来看，logistic函数时一种比较理想的算法。算法中对梯度上升法进行了一些改进，使得收敛速度更快，使得算法的可行性有了大大提高。但是通过实例分析，分类的效果并不如预期的效果那么好。算法中是否还存在能够改进的地方，值得进一步探究。