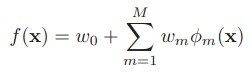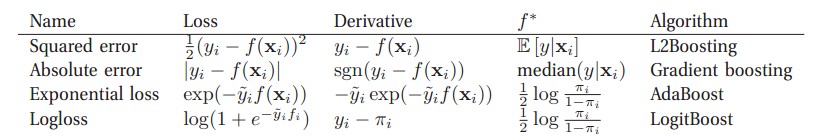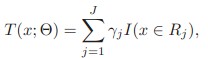GBDT(Gradient Boosting Decision Tree) 没有实现仅仅有原理
阿弥陀佛。好久没写文章,实在是受不了了。特来填坑,近期实习了(ting)解(shuo)到(le)非常多工业界经常使用的算法。诸如GBDT,CRF,topic model的一些算法等。也看了不少东西。有时间能够具体写一下,而至于实现那真的是没时间没心情再做了,等回学校了再说吧。今天我们要说的就是GBDT(Gradient Boosting Decision Tree)
=======================================================================
〇.前序
GBDT是看一个大牛团队做推荐算法比赛的时候拿这个模型来处理最后得到的全部的feature并输出结果的模型。想到自己曾经天真地拿着SVD单模型调參參加这类比赛的时候真是……闻者伤心,听着流泪啊,别的不谈。这次讲GBDT主要是由于了解GBDT的一些前置条件我都在博客里写过,能够直接跳到关键部分开写……进入正题吧
一.前置条件
1.决策树
參看我曾经的一篇博客:http://blog.csdn.net/dark_scope/article/details/13168827
尽管里面写的都是决策分类树。而我们这次主讲的是决策回归树,只是事实上都差点儿相同,决策回归树呢就是把分到某个分支上的全部训练例子的目标值求平均或者取中位数返回而已。
2.boosting
一般来说哦讲boosting都以adaboost这个特例開始讲,所以你能够先看一看我的这篇博客:AdaBoost--从原理到实现
然后我们来接着讲boosting……新开一章吧。这个事实上是主要内容
二.boosting 提升方法
提升方法事实上是一个比adaboost概念更大的算法,由于adaboost能够表示为boosting的前向分布算法(Forward stagewise additive modeling)的一个特例。boosting终于能够表示为:
当中的w是权重,Φ是弱分类器(回归器)的集合,事实上就是一个加法模型(即基函数的线性组合)
前向分布算法 实际上是一个贪心的算法,也就是在每一步求解弱分类器Φ(m)和其參数w(m)的时候不去改动之前已经求好的分类器和參数:

为了表示方便。我们以后用β取代w进行描写叙述了,图中的b是之前说的Φ弱分类器
OK,这也就是提升方法(之前向分布算法)的大致结构了。能够看到当中存在变数的部分事实上就是极小化损失函数 这关键的一步了。怎样选择损失函数决定了算法的终于效果(名字)……这一步你能够看出算法的“趋势”。以后再单独把“趋势”拿出来说吧。由于我感觉理解算法的关键之中的一个就是理解算法公式的“趋势”
三.各种提升方法
不同的损失函数和极小化损失函数方法决定了boosting的终于效果。我们如今来说几个常见的boosting:
(图自 Machine Learning A Probabilistic Perspective)对于二分类问题来说:当中πi=sigm(2f(xi)) ,y~i∈{-1,+1},yi∈{0,1}
广义上来讲,所谓的Gradient Boosting 事实上就是在更新的时候选择梯度下降的方向来保证最后的结果最好。一些书上讲的“残差” 方法事实上就是L2Boosting吧,由于它所定义的残差事实上就是L2Boosting的Derivative。接下来我们着重讲一下弱回归器(不知道叫啥了,自己编的)是决策树的情况,也就是GBDT。(不知道为何上表的Absolute被命名为了Gradient boosting,关于Gradient boosting在后面会有更仔细的介绍)
四.GBDT
对于决策树,事实上能够把它表示为下式。即是把特征空间划分为多个区域,每一个区域返回某个值作为决策树的预測值
当中Rj是区域,γ是返回值,I()在当中的条件成立情况下为1。否则为0.当中的參数J能够大概看做树的深度的一个表示,这是一个待调的參数
我们知道Gradient Boosting最重要的一步就是去拟合下式:
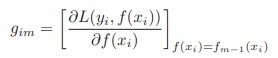
对于不同的Loss function,其梯度有不同的表达式:
(图自The Elements of Statisic Learning)
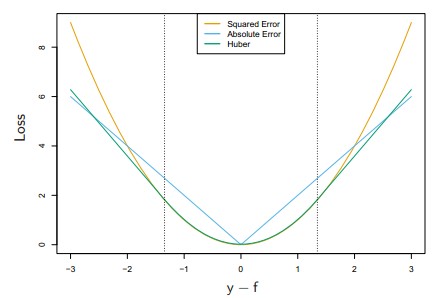
前三种相应的loss function例如以下图:当中Huber是低于某个值表现为square error,高于某个值则表现为线性
以下是GBDT的大概框架:(Gradient Tree Boosting应该是GBDT还有一种说法,有误请指正)
(算法自The Elements of Statistical Learning )
整个框架描写叙述得事实上已经非常清晰了,就不在这里赘述了,总之所谓Gradient就是去拟合Loss function的梯度,将其作为新的弱回归树增加到总的算法中就可以。
五.尾巴
本文大概写了一下GBDT的框架和原理。兴许事实上还有涉及到參数的选择(如树的深度)。正则化(regularization)等内容。主要是在实现的时候要注意。有时间会写一份toy代码出来。
【Reference】
【1】《The Elements of Statistical Learning 》
【2】《统计学习方法》
【3】《Machine Learning A Probabilistic Perspective》
posted on 2019-04-24 13:19 xfgnongmin 阅读(185) 评论(0) 编辑 收藏 举报