随想--割点和强连通分量T算法的区别

哈！大家好！

几天前纠结的问题——“割点程序中，子结点写low(u)=min{low(u),low(v)}，非父祖先写low(u)=min{low(u),dfn(v)}”我搞懂了！但是今天看了看和割点程序几乎一样的强连通分量T算法，又在那问题上绊住了……

---

 

先说说我对割点那问题的理解——

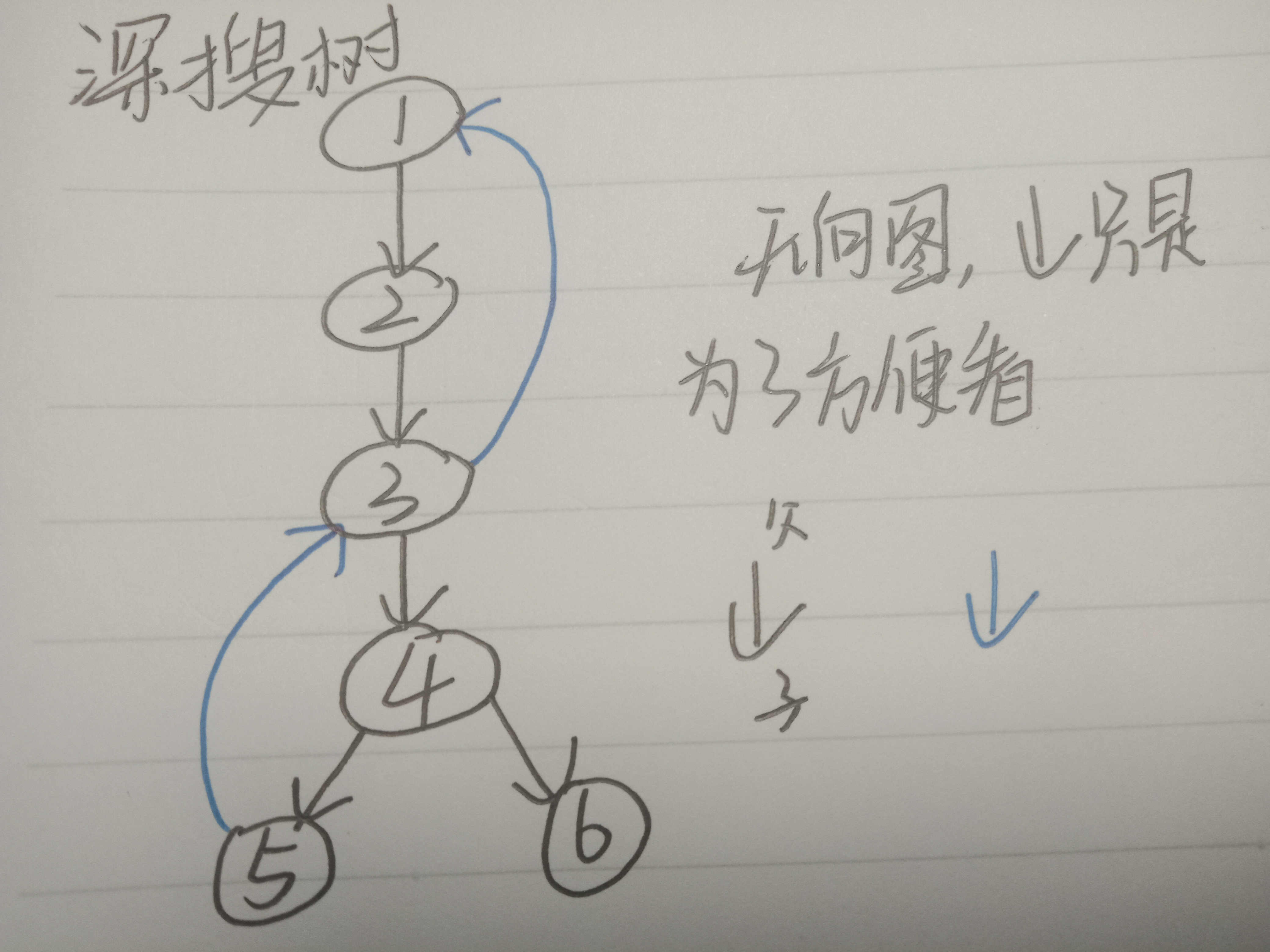
这幅图是我把图按深搜顺序转化成了树！叫他深搜树吧！

5能到3，且3非5父（祖先），则low5=dfn3。但按照我的错误想法low5=low3=1（low3已经等于1），那么5返回4时，low4=low5=1，但4到达这个1经过了4的父节点！

所以说“割点程序中，子结点写low(u)=min{low(u),low(v)}，非父祖先写low(u)=min{low(u),dfn(v)}”

(这是我自己的想法，自己觉得挺对的，也不知道对不对，也不知道说的清不清楚）

---

 

前两天刚接触这个T算法时，我觉得原理什么都和割点一模一样吧！low dfn那样写当时也就没多想

但是——

割点是求一个点，而强是求一个整体。所以割点中low是为了判断这个点不经父能否到达祖先，毫无疑问。但强里low是什么意思？看看书，没懂。我又举样例发现一个强连通分量里不是所有结点的low都等于子树根结点的dfn！所以我就感觉这个low变化就是让low不等于自身的dfn（除根）。但如果两个都写成low(u)=min{low(u),low(v)}会出什么问题？我还不知道。

写得挺乱qwq