To_Heart—总结——最短路
最短路问题(short-path problem):最短路问题是图论研究中的一个经典算法问题,指在寻找图(由结点和路径组成的)中两结点之间的最短路径。算法具体的形式包括:
1.确定起点的最短路径问题 - 即已知起始结点,求最短路径的问题。
2.确定终点的最短路径问题 - 与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题。在无向图中该问题与确定起点的问题完全等同,在有向图中该问题 等同于把所有路径方向反转的确定起点的问题。
3.确定起点终点的最短路径问题 - 即已知起点和终点,求两结点之间的最短路径。
4.全局最短路径问题 - 求图中所有的最短路径。
以一个故事开头吧:
这又是晴朗的一天,XF准备去旅行,但他这次想去看自由男神像。所以他正在用千度查一查机票的价格:
出发地 目的地 单价
夫代尔马 自由男神像 15000 yuan
浮卢宫 尼悉歌剧院 100 yuan
尼悉歌剧院 自由男神像 1000 yuan
夫代尔马 浮卢宫 10 yuan
XF现在住在夫代尔马,他发现直接由夫代尔马去自由男神像会比夫代尔马->浮卢宫->尼悉歌剧院->自由男神像花费的钱多一些,~~或者说,多得多。。。~~所以他决定选择
夫代尔马->浮卢宫->尼悉歌剧院->自由男神像这一条便宜的方案!!!
故事结束!
那么,我们把XF的机票选择方案扩大很多很多倍,且让XF住的地方变来变去,就成为了求一个多源最短路径的题啦!!
那么对于这类问题,我们应该砸么做类??
Floyd算法隆重出场!!!
首先,我要问一个问题:为什么两个顶点的最短距离为什么不是它们的直接距离呢???
局外读者:“因为他们有可能没有直接连接的边,而是由一个或多个中继顶点间接连接的啊!!!”
对啦!真聪明!!!
举个栗子:
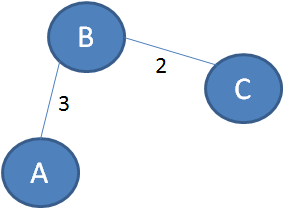
上图的顶点A和顶点C没有直接相连的边,它们之间没有直接距离。
如果以B作为“中继顶点”,此时A到C的最短路径就是A-B-C,最短距离是3+2=5
那么,再举个栗子:
上图的顶点A和顶点C直接相连,距离是6。但是存在一条“迂回”路径A-B-C,距离是3+2=5<6。
所以,经过中继顶点B,从A到C的最短距离是5。
这就是弗洛伊德算法的核心思想,我们利用这些中继顶点,一步一步推导出图中所有顶点的最短距离;
下面我们来看一看Floyd算法的详细步骤。
- 要实现Floyd算法,首先需要构建带权图的邻接矩阵:
在邻接矩阵当中,每一个数字代表着从某个顶点到另一个顶点的直接距离,这个距离是没有涉及到任何中继顶点的。 - 此时假定只允许以顶点A作为中继顶点,那么各顶点之间的距离会变成什么样子呢?
B和C之间的距离原本是无穷大,此时以A为中继,距离缩短为AB距离+AC距离=
5+2=7。
更新对应矩阵元素(橙色区域代表顶点A到其他顶点的临时距离:

- 接下来以顶点A、B作为中继顶点,那么各顶点之间的距离会变成什么样子呢?
A和D之间的距离原本是无穷大,此时以B为中继,距离缩短为AB距离+BD距离=5+1=6。
A和E之间的距离原本是无穷大,此时以B为中继,距离缩短为AB距离+BE距离=5+6=11。
更新对应矩阵元素(橙色区域代表顶点B到其他顶点的临时距离):

- 接下来以顶点A、B、C作为中继顶点,那么各顶点之间的距离会变成什么样子呢?
A和F之间的距离原本是无穷大,此时以C为中继,距离缩短为AC距离+CF距离=2+8=10。
更新对应矩阵元素(橙色区域代表顶点C到其他顶点的临时距离):
以此类推,我们不断引入新的中继顶点,不断刷新矩阵中的临时距离。
最终,当所有顶点都可以作为中继顶点时,我们的距离矩阵更新如下:

此时,矩阵中每一个元素,都对应着某顶点到另一个顶点的最短距离。
让我们回顾一下动态规划的两大要素:
问题的初始状态
问题的状态转移方程式
对于寻找图的所有顶点之间距离的问题,初始状态就是顶点之间的直接距离,也就是邻接矩阵。
而问题的状态转移方程式又是什么呢?
假设新引入的中继顶点是n,那么:
顶点i 到 顶点j 的新距离 = Min(顶点i 到 顶点j 的旧距离,顶点i 到 顶点n 的距离+顶点n 到 顶点j 的距离
所以:
弗洛伊德是一种基于动态规划的多源点最短路算法!
回到故事,如果XF就一直住在夫代尔马呢??
那么,这就转换为一道单源最短路径问题了。。。
Dijkstra算法隆重出场!!!
究竟什么是迪杰斯特拉算法?它是如何寻找图中顶点的最短路径呢?
这个算法的本质,是不断刷新起点与其他各个顶点之间的 “距离表”。
让我们来演示一下迪杰斯特拉的详细过程:
-
,创建距离表。表中的Key是顶点名称,Value是从起点A到对应顶点的已知最短距离。但是,一开始我们并不知道A到其他顶点的最短距离是多少,Value默认是无限大

-
,遍历起点A,找到起点A的邻接顶点B和C。从A到B的距离是5,从A到C的距离是2。把这一信息刷新到距离表当中:

-
,从距离表中找到从A出发距离最短的点,也就是顶点C。
-
,遍历顶点C,找到顶点C的邻接顶点D和F(A已经遍历过,不需要考虑)。从C到D的距离是6,所以A到D的距离是2+6=8;从C到F的距离是8,所以从A到F的距离是2+8=10。把这一信息刷新到表中:

接下来重复第3步、第4步所做的操作: -
,也就是第3步的重复,从距离表中找到从A出发距离最短的点(C已经遍历过,不需要考虑),也就是顶点B。
-
,也就是第4步的重复,遍历顶点B,找到顶点B的邻接顶点D和E(A已经遍历过,不需要考虑)。从B到D的距离是1,所以A到D的距离是5+1=6,小于距离表中的8;从B到E的距离是6,所以从A到E的距离是5+6=11。把这一信息刷新到表中:(在第6步,A到D的距离从8刷新到6,可以看出距离表所发挥的作用。距离表通过迭代刷新,用新路径长度取代旧路径长度,最终可以得到从起点到其他顶点的最短距离)

-
,从距离表中找到从A出发距离最短的点(B和C不用考虑),也就是顶点D。
-
,遍历顶点D,找到顶点D的邻接顶点E和F。从D到E的距离是1,所以A到E的距离是6+1=7,小于距离表中的11;从D到F的距离是2,所以从A到F的距离是6+2=8,小于距离表中的10。把这一信息刷新到表中:

(过了一百年——————)

就这样,除终点以外的全部顶点都已经遍历完毕,距离表中存储的是从起点A到所有顶点的最短距离。显然,从A到G的最短距离是11。(路径:A-B-D-F-G)
弗洛伊德代码实现:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int n,m,x,y;
long long dp[505][505];
int pre[505][505];
void HH(int z){
if(pre[x][z]==0)
return ;
HH(pre[x][z]);
printf("%d ",z);
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++)
dp[i][j]=214748360;
}
for(int i=1;i<=m;i++){
int sum;
cin>>x>>y>>sum;
dp[x][y]=sum;
pre[x][y]=x;
}
for(int k=1;k<=n;k++){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(dp[i][j]>dp[i][k]+dp[k][j]){
dp[i][j]=dp[i][k]+dp[k][j];
pre[i][j]=pre[k][j];
}
}
}
}
cin>>x>>y;
cout<<dp[x][y]<<endl;
printf("%d ",x);
HH(y);
return 0;
}
Dijkstra算法:
#include<bits/stdc++.h>
using namespace std;
int n,m,x,y;
bool flag[5005]={};
int dp[5005][5005],f[5005];
int main(){
cin>>n>>m>>x>>y;
memset(dp,0x3f,sizeof(dp));
memset(f,0x3f,sizeof(f));
for(int i=1;i<=m;i++){
int xx,yy,zz;
scanf("%d %d %d",&xx,&yy,&zz);
dp[xx][yy]=dp[yy][xx]=zz;
}
f[x]=0;
flag[x]=0;
for(int i=1;i<=n;i++){
int Minn=0x3f3f3f3f;
int k=0;
for(int j=1;j<=n;j++){
if(flag[j]==0&&(f[j]<Minn)){
Minn=f[j];
k=j;
}
}
if(k==0) continue;
flag[k]=1;
for(int j=1;j<=n;j++){
if(f[j]>f[k]+dp[k][j]){
f[j]=f[k]+dp[k][j];
}
}
}
printf("%d",f[y]);
return 0;
}

