1136 欧拉函数

知识点：

       素数是只能被1或自身整除的自然数。一般的，1不算素数。

       对正整数n，欧拉函数是少于或等于n的数中与n互质的数的数目。

       欧拉函数通式：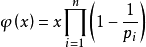

 

题目链接：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1136

题目分析：先质因数分解，如果是素数则欧拉函数即是自身。否则带入公式即可。

题解代码：

#include<stdio.h>
#include<stdlib.h>
#include<algorithm>
#include<string.h>
#include<set>
#include<vector>
#include<math.h>
#include<iostream>
std::vector<int> prim;
int isprim(int x)
{
    int t = 2;
    int copy = x;
    for (int i = 2; i <= x; i++)
    {
        if (x%i == 0)
        {
            x /= i;
            while (x%i == 0)
                x /= i;
            prim.push_back(i);
        }
    }
    if (prim.back() != copy)
        return 0;//不是素数
    else
        return 1;//是素数
}
int main()
{
    int n;
    scanf("%d", &n);
    if (isprim(n))
        printf("%d\n", n);
    else
    {
        int temp = n;
        for (int i = 0; i < prim.size(); i++)
            temp = temp / prim[i];
        for (int i = 0; i < prim.size(); i++)
            temp = temp*(prim[i] - 1);
        printf("%d\n", temp);
    }
}