N皇后问题

问题描述：

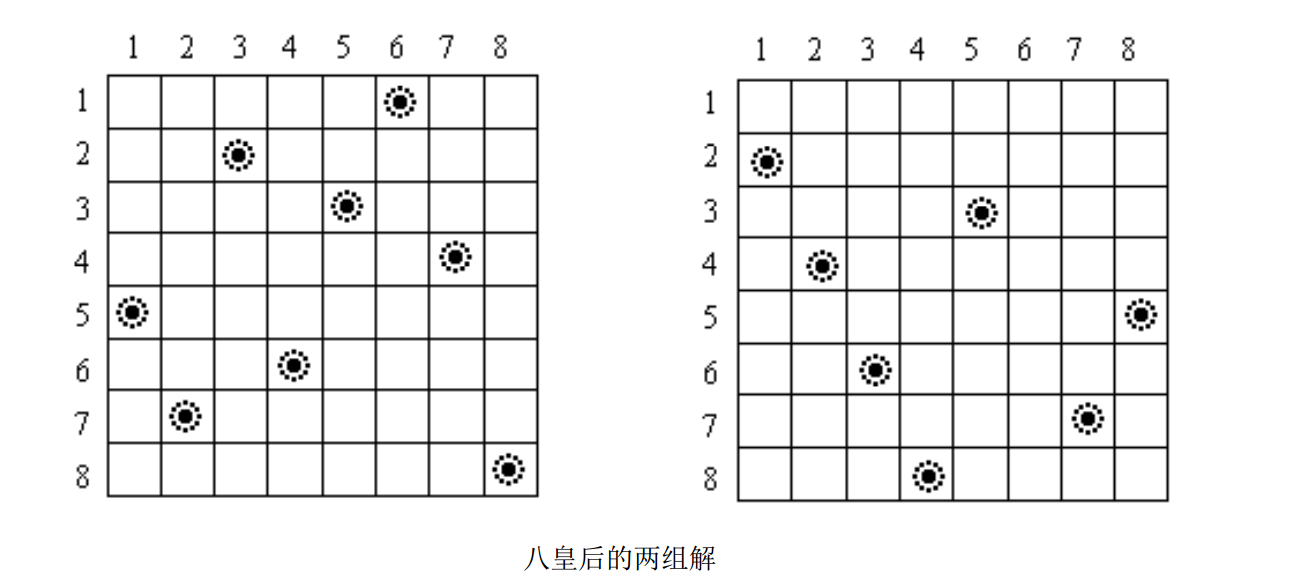
在 N*N 的棋盘上放置 N 个皇后（n<=10）而彼此不受攻击（即在棋盘的任一行，任一列和任一对角线上
不能放置 2 个皇后），编程求解所有的摆放方法。

输入

输入：n

输出

每行输出一种方案，每种方案顺序输出皇后所在的列号，各个数占5个字符。若无方案，则输出
no solute!

样例输入

4

复制

样例输出

    2    4    1    3
    3    1    4    2
解题过程：
我的第一印象是做四个数组a,b,c,d分别表示横纵斜
然后做一个两个for循环的长度为N（棋盘宽度）的深搜
但是我调试了好久，没把结构调试好。。
然后，（偷看课本）我才知道一个更简洁的思路：
dfs回溯本身就可以替换一个for循环，同时还能顶替a数组（递归层数表示行数）
代码：

#include<bits/stdc++.h>
using namespace std;
int dfs(int);
void coout(int);
int a[50],b[50],c[50],d[50],e[50];
int jishuqi=0,n;
int main()
{
cin>>n;
dfs(1);
return 0;
}
int dfs(int i)
{
for(int j=1;j<=n;j++)
{
if((b[j]==0)&&(c[i+j]==0)&&(d[i-j+n-1]==0))
{
a[i]=j;b[j]=1;c[i+j]=1;d[i-j+n-1]=1;
if(i==n) coout(i);
else dfs(i+1);b[j]=0;c[i+j]=0;d[i-j+n-1]=0;
}
//
}
// return dfs(k-1);

}
void coout(int l)
{
for(int i=1;i<=n;i++)
cout<<setw(5)<<a[i];
cout<<endl;

}
// for(int i=1;i<=n;i++)
// {
// if((a[i]!=0)&&(b[i]!=0)&&(c[i]!=0)&&(d[i]!=0))
// {
// a[i]=1;b[i]=1;c[i]=1;d[i]=1;
// }
// else continue;
// }
// if()

//后面部分是我一开始做的（但不对）

return 0；