背包问题

1.01背包

一个旅行者有一个最多能装 M 公斤的背包，现在有 n 件物品，它们的重量分别是W1，W2，…,Wn,它们的价值分别为C1,C2,…,Cn，求旅行者能获得最大总价值。

输入

第一行：两个整数，M(背包容量，M<=200)和N(物品数量，N<=30)；

第2…N+1行：每行二个整数Wi，Ci，表示每个物品的重量和价值。

输出

仅一行，一个数，表示最大总价值。

样例输入

10 4
2 1
3 3
4 5
7 9

复制

样例输出

12

其实就是每件物品放与不放的问题，第一种是用的二维数组，打个表（真打表）

 

 

 

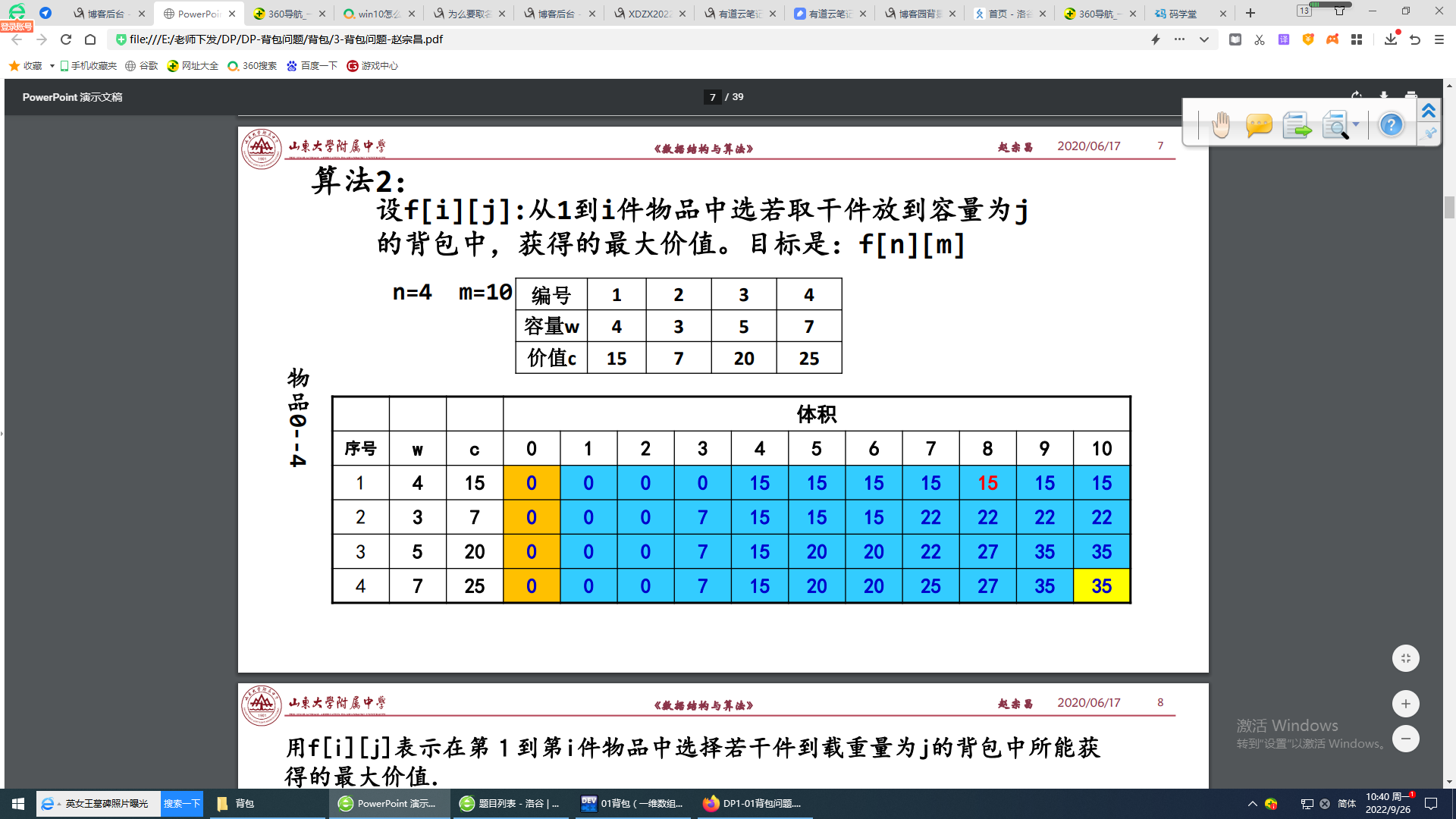
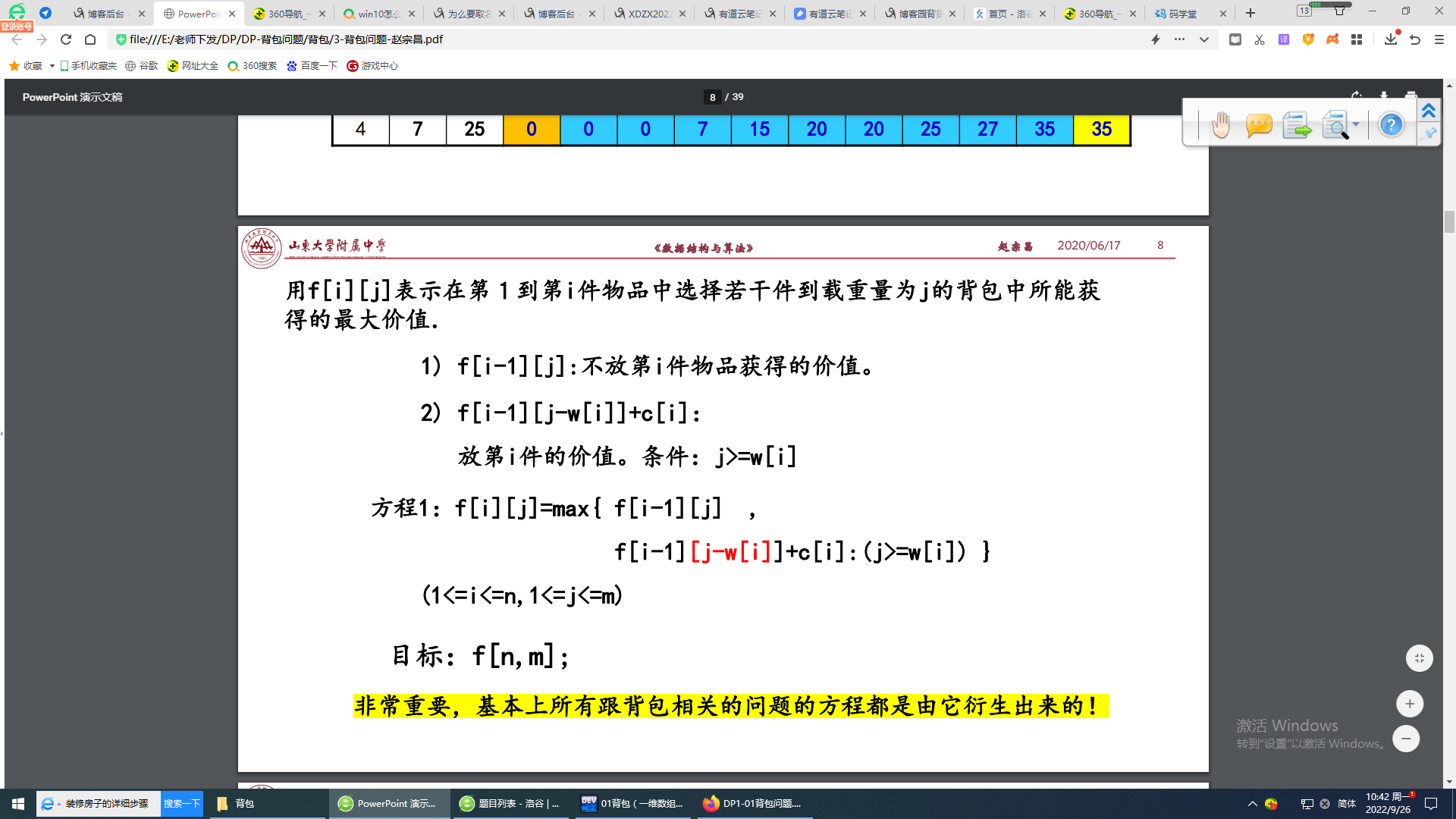
 代码如下

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int maxw,n;
int w[110],v[110],dp[110][20010];

int main()
{
    cin>>maxw>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i];
        for(int j=1;j<=maxw;j++)
        {
           if(w[i]<=j)
           {
           dp[i][j]=max(dp[i-1][j],v[i]+dp[i-1][j-w[i]]);               
           }
            else
           {
            dp[i][j]=dp[i-1][j];
           }
        }
    }
    cout<<dp[n][maxw]<<endl;
    return 0;
}

第二种是一维数组

 

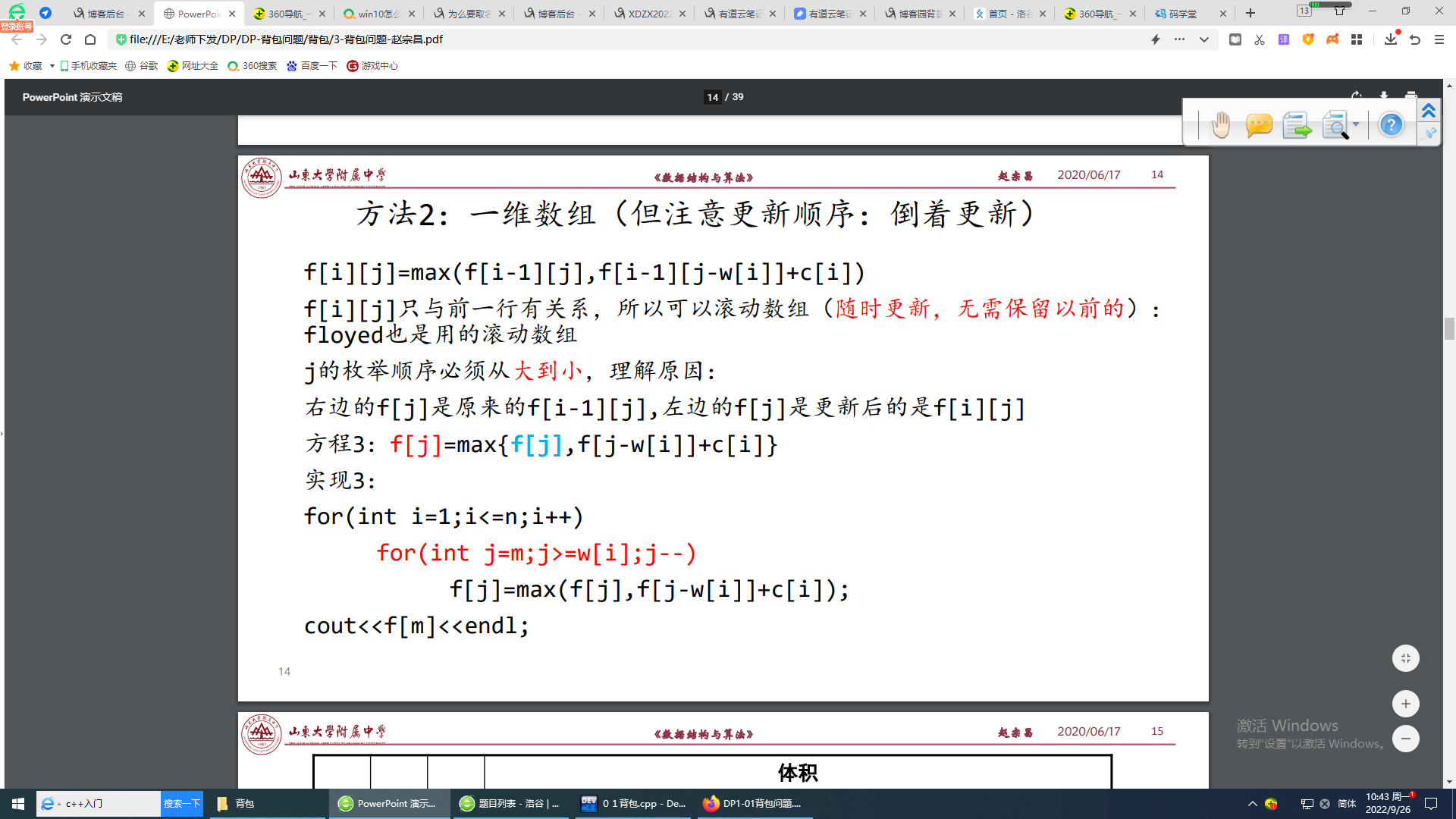
 代码

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int maxw,n;
int w[110],v[110],dp[205];

int main()
{
    cin>>maxw>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i];
        for(int j=1;j<=maxw;j++)
        {
           if(w[i]<=j)
               dp[j]=max(dp[j],dp[j-w[i]]+v[i]);                                      
        }
    }
    cout<<dp[maxw]<<endl;
    return 0;
}

2.完全背包

设有n种物品，每种物品有一个重量及一个价值。但每种物品的数量是无限的，同时有一个背包，最大载重量为M，今从n种物品中选取若干件(同一种物品可以多次选取)，使其重量的和小于等于M，而价值的和为最大。

输入

第一行：两个整数，M(背包容量，M≤200)和N(物品数量，N≤30)；
第2…N+1行：每行二个整数Wi,Ci，表示每个物品的重量和价值。

输出

仅一行，一个数，表示最大总价值。

样例输入

10 4
2 1
3 3
4 5
7 9

复制

样例输出

max=12

完全背包与01背包的差别其实就是可以取无限个物品，而01背包一件物品只能取一个

 

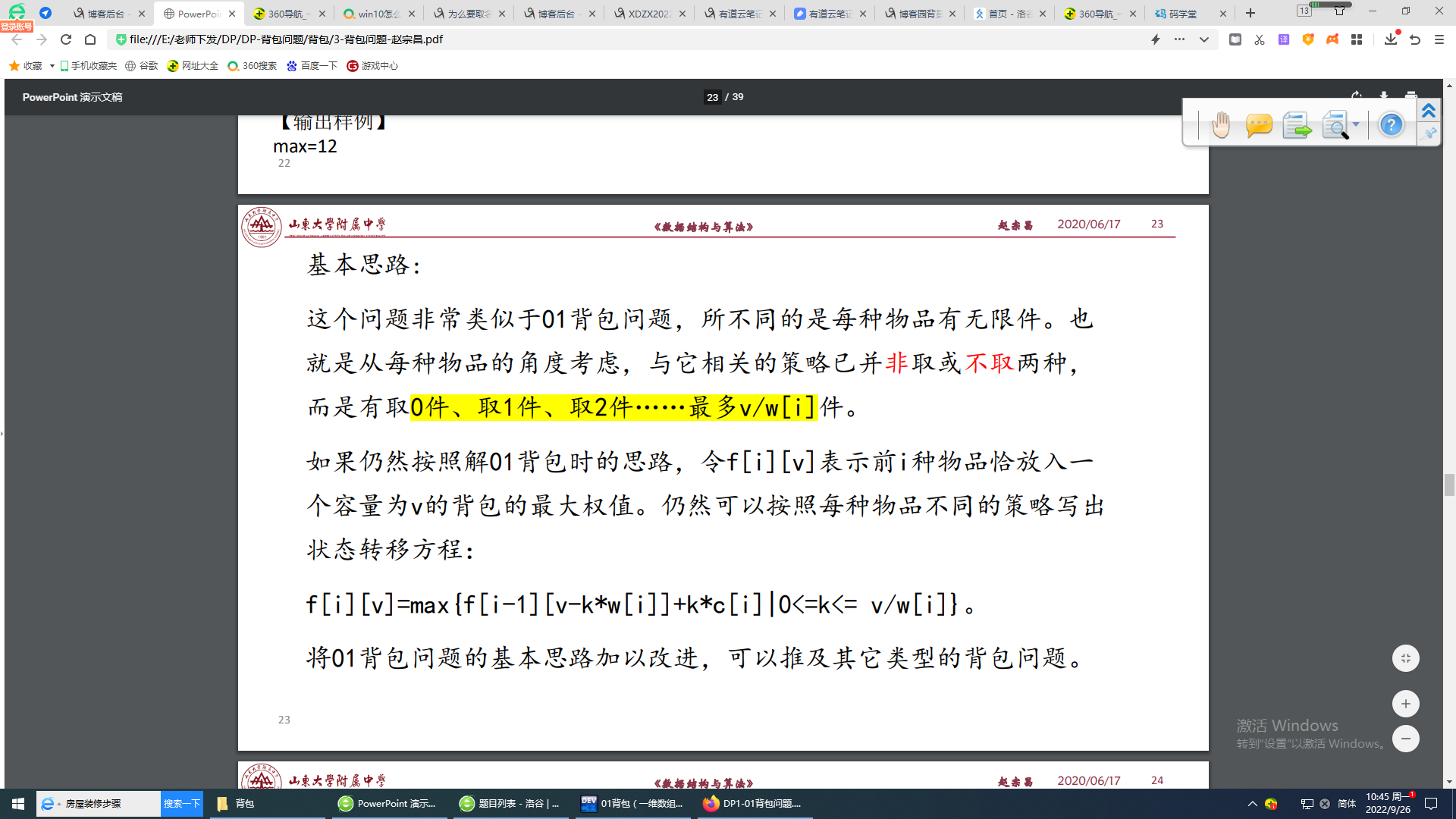
 变动其实并不大，没必要太多解释

代码

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int maxw,n;
int w[110],v[110],dp[110];

int main()
{
    cin>>maxw>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>w[i]>>v[i];
        for(int j=w[i];j<=maxw;j++)
        {
              dp[j]=max(dp[j],dp[j-w[i]]+v[i]);               
        }
    }
    cout<<"max="<<dp[maxw]<<endl;
    return 0;
}

3.多重背包

（没怎么搞，有时间在搞吧）

背包问题还有很多种，要学会转换！