N 皇后问题

N 皇后问题

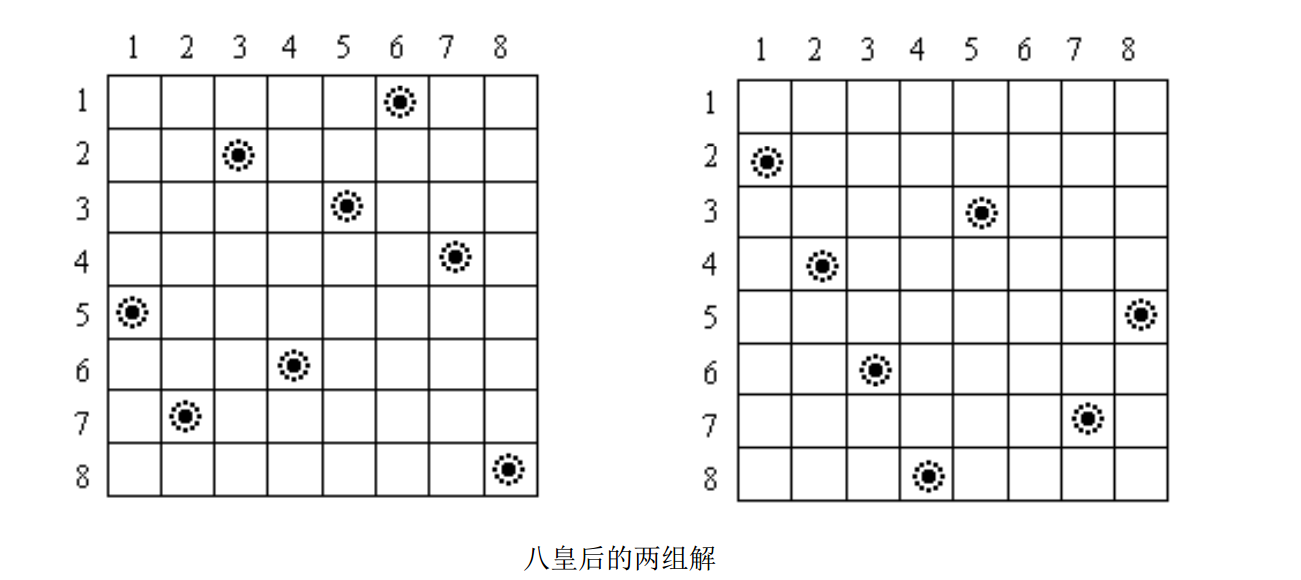
题目描述：在 N*N 的棋盘上放置 N 个皇后（n<=10）而彼此不受攻击（即在棋盘的任一行，任一列和任一对角线上
不能放置 2 个皇后），编程求解所有的摆放方法

输入

输入：n

输出

每行输出一种方案，每种方案顺序输出皇后所在的列号，各个数占5个字符。若无方案，则输出
no solute!

样例输入

4

复制

样例输出

    2    4    1    3
    3    1    4    2


思路：也是一道非常经典的深搜题目了。这是一个类似于枚举的过程：每一行每一行地进行尝试，如果没有皇后能侵犯到自己， 就放置该棋子，同时占据她所能占据的所有领地。最后，在每一行上都各有一个皇后时，就输出答案。最难处理的地方就是对对角线的处理，需要考虑很多东西。代码如下：

#include<bits/stdc++.h>
using namespace std;
int a[101],b[101],c[101],d[101]; //a代表行，b代表列，c代表左下到右上的对角线，d代表左上到右下的对角线 
int n,ans=0; //ans记录方案总数 ，n要全局变量，搜索要用 
void print()  //输出函数 
{
    for(int i=1;i<=n;i++)
    {
        cout<<"    "<<a[i];
    }
    cout<<endl;
    ans++;
}
void queen(int i)  
{
    int j;
    if(i>n)   
    {
        print();
        return;   
    }
    else 
{
    for(j=1;j<=n;j++) //经过每个位置 
    {
        if((!b[j])&&(!c[i+j])&&(!d[i-j+n])) //如果没有皇后占领，就执行 
        {
            a[i]=j; //标记i排是第j个 
            b[j]=1; //宣布占领纵列 
            c[i+j]=1;
            d[i-j+n]=1; //宣布占领两条对角线 
            queen(i+1); //下一个皇后 
            b[j]=0;  
            c[i+j]=0;
            d[i-j+n]=0;//回溯 
        }
    }
}
    
}
int main()
{
    cin>>n; //输入N*N的网络 
    queen(1);  
    if(ans==0)    cout<<"no solute!"<<endl; //如果没有方案的话则输出 
    //else cout<<ans;
    return 0;
 }