排序算法（七）非比较排序：计数排序、基数排序、桶排序

 

前面讲的是比较排序算法，主要有冒泡排序，选择排序，插入排序，归并排序，堆排序，快速排序等。

非比较排序算法：计数排序，基数排序，桶排序。在一定条件下，它们的时间复杂度可以达到O(n)。

一，计数排序（Counting Sort）

(1)算法简介

计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

(2)算法描述和实现

1. 得到待排序数的范围（在这里增加了上界和下界）；
2. 统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
3. 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加），计算得到每个元素在排序后数组中的结束位置；
4. 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

实现

public static void countSort(int[] array, int downBound, int upperBound) {  
    int[] countArray = new int[upperBound - downBound + 1];  
    if (upperBound < downBound)  
        return;  
    for (int i = 0; i < array.length; i++) {  
        countArray[array[i] - downBound]++;  
    }  
    int posSum = 0;  
    for (int i = 0; i < upperBound - downBound + 1; i++) {  
        posSum += countArray[i];  
        countArray[i] = posSum;  
    }  
    int[] result = new int[array.length];  
    for (int i = array.length - 1; i >= 0; i--) {  
        result[countArray[array[i] - downBound] - 1] = array[i];  
        countArray[array[i] - downBound]--;  
    }  
    for (int i = 0; i < array.length; i++) {  
        array[i] = result[i];  
    }  
}  

(3)算法分析

当输入的元素是n 个0到k之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存（如果数据比较分散，则在countArray中其实是有大量0的，占用很多空间）。

最佳情况：T(n) = O(n+k)
最差情况：T(n) = O(n+k)
平均情况：T(n) = O(n+k)

二，桶排序（Bucket Sort）

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。

(1)算法简介

桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排。

(2)算法描述和实现

1. 设置一个定量的数组当作空桶；
2. 遍历输入数据，并且把数据一个一个放到对应的桶里去；
3. 对每个不是空的桶进行排序；
4. 从不是空的桶里把排好序的数据拼接起来。

实现

public static void bucketSort(int[] arr){  
      
    int max = Integer.MIN_VALUE;  
    int min = Integer.MAX_VALUE;  
    for(int i = 0; i < arr.length; i++){  
        max = Math.max(max, arr[i]);  
        min = Math.min(min, arr[i]);  
    }  
      
    //桶数  
    int bucketNum = (max - min) / arr.length + 1;  
    ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);  
    for(int i = 0; i < bucketNum; i++){  
        bucketArr.add(new ArrayList<Integer>());  
    }  
      
    //将每个元素放入桶  
    for(int i = 0; i < arr.length; i++){  
        int num = (arr[i] - min) / (arr.length);  
        bucketArr.get(num).add(arr[i]);  
    }  
      
    //对每个桶进行排序  
    for(int i = 0; i < bucketArr.size(); i++){  
        Collections.sort(bucketArr.get(i));  
    }  
｝     

 下图给出了对{ 29, 25, 3, 49, 9, 37, 21, 43 }进行桶排序的简单演示过程

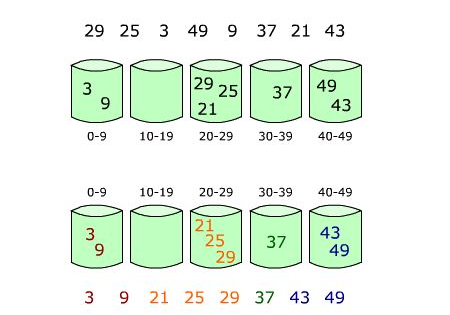
(3)算法分析

桶排序最好情况下使用线性时间O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

最佳情况：T(n) = O(n+k)
最差情况：T(n) = O(n+k)
平均情况：T(n) = O(n2)

三，基数排序（Radix Sort）

(1)算法简介

基数排序是按照低位先排序，然后收集（就是按低位排序）；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。

(2)算法描述和实现

1. 取得数组中的最大数，并取得位数；
2. arr为原始数组，从最低位开始取每个位组成radix数组；
3. 对radix进行计数排序（利用计数排序适用于小范围数的特点）；

public static void radixSort(int[] array, int maxDigit) {  
    int len = array.length;  
    int digitCount = 1;  
    int digitDev = 1;  
    int[] tmp = new int[len];  
    int[] count = new int[10];  
    while (digitCount <= maxDigit) {  
        Arrays.fill(count, 0);  
        Arrays.fill(count, 0);  
        for (int i = 0; i < len; i++) {  
            count[(array[i] / digitDev) % 10]++;  
        }  
        int sum = 0;  
        for (int i = 1; i < 10; i++) {  
            count[i] = count[i] + count[i - 1];  
        }  
        for (int i = len - 1; i >= 0; i--) {  
            tmp[count[(array[i] / digitDev) % 10] - 1] = array[i];  
            count[(array[i] / digitDev) % 10]--;  
        }  
        for (int i = 0; i < len; i++) {  
            array[i] = tmp[i];  
        }  
        digitDev *= 10;  
        digitCount++;  
    }  
}  

下图给出了对{ 329, 457, 657, 839, 436, 720, 355 }进行基数排序的简单演示过程

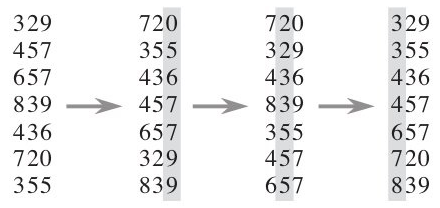
(3)算法分析

最佳情况：T(n) = O(n * k)
最差情况：T(n) = O(n * k)
平均情况：T(n) = O(n * k)

 

基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

基数排序：根据键值的每位数字来分配桶
计数排序：每个桶只存储单一键值
桶排序：每个桶存储一定范围的数值

参考：

http://www.cnblogs.com/eniac12/p/5332117.html

https://www.cnblogs.com/jztan/p/5878630.html

http://blog.csdn.net/wangqyoho/article/details/52584640