排序算法（六）快速排序

　　快速排序算法最早由图灵奖获得者 Tony Hoare 设计出来的，被列为 20 世纪十大算法之一。在C++ STL 、Java SDK等开发工具包的源码中都能找到它的某种实现版本。

　　希尔排序相当于直接插入排序的升级，它们同属于插入排序类，堆排序相当于简单选择排序的升级，它们同属于选择排序类。而快速排序其实就是我们前面认为最慢的冒泡排序的升级，它们都属于交换排序类。即官也是通过不断比较和移动交换来实现排序的，只不过宫的实现，增大了记景的比较和移动的距离，将关键字较大的记录从前面直接移动到后面，关键字较小的记录从后面直接移动到前面，从而减少了总的比较次数和移动交换次数。

1，算法描述

快速排序 ( Quick Sort) 的基本思想是:通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序的目的。

2，实现步骤

从序列中挑出一个元素，作为"基准"(pivot).
把所有比基准值小的元素放在基准前面，所有比基准值大的元素放在基准的后面（相同的数可以到任一边），这个称为分区(partition)操作。
对每个分区递归地进行步骤1~2，递归的结束条件是序列的大小是0或1，这时整体已经被排好序了。

　　实现

 1 private static void quickSort(int[] arr,int start,int end){  
 2         if(start<end){
 3             int keyIndex = partition(arr, start, end);//原始数组选的主元现在所在的位置索引
 4             quickSort(arr, start, keyIndex-1);//对主元左侧的序列进行快速排序    
 5             quickSort(arr, keyIndex+1, end);//对主元右侧的序列进行快速排序    
 6         }  
 7     }  
 8     
 9     /** 
10      * 本函数实现一趟快速排序，以数组的第一个元素为主元
11      * ！！！本函数运行结束后使得主元左侧的元素小于主元，主元右侧的元素大于主元。 
12      * @param arr 待排序的数组 
13      * @return 返回经一趟排序后主元的下标 j
14      */ 
15     public static int partition(int[] arr, int start, int end){
16         int key = arr[start];//把数组第一个元素设为主元(如果需要优化可以从arr中随机一个数作为主元)
17         int i = start;//两个指针，i指向数组头，j指向数组尾
18         int j = end;    
19         while(i < j){//若i与j未相遇，则执行以下循环
20             while(arr[j] >= key && j > start){//j从右向左扫描，直到当前元素小于主元素停下
21                 j--;
22             }
23             while(arr[i] <= key && i < end){//i从左向右扫描，直到当前元素大于主元时停止
24                 i++;
25             }
26             if(i < j)//因为上述扫描有可能发生i>j的情况
27                 swap(arr, i, j);
28         }
29         swap(arr, start, j);//将主元与j交换
30         return j;        
31     }
32     
33     private static void swap(int[] arr, int i, int j) {
34         int temp = arr[i];
35         arr[i] = arr[j];
36         arr[j] = temp;    
37     }

3，算法优化

优化选取枢轴（主元），选取的该值最好每次都在待排序列的中间值附近，如果选的主元是最大值，每次调用就只是进行了第29行的一次交换。

1）随机选取枢轴（主元），感觉是在碰运气。
2）三数取中法，靠谱一点，就是从序列的前，中，后取三个元素，中间的作为主元。

4，算法分析

快速排序比较适合大量数据的排序，如果序列元素个数小于7（有资料认为 7 比较合适，也有认为 50 更合理，实际应用可适当调整) ，不如直接用插入排序。

时间复杂度：

最佳情况：T(n) = O(nlogn)

最差情况：T(n) = O(n^2)

平均情况：T(n) = O(nlogn)

时间复杂度计算过程：http://blog.csdn.net/wangqyoho/article/details/52584640

空间复杂度：

O(log(n)）

稳定性：不稳定

5，应用

Java SDK提供的Arrays.sort函数。对于基础类型，底层使用快速排序。对于非基础类型，底层使用归并排序。请问是为什么？

答：这是考虑到排序算法的稳定性。对于基础类型，相同值是无差别的，排序前后相同值的相对位置并不重要，所以选择更为高效的快速排序，尽管它是不稳定的排序算法；而对于非基础类型，排序前后相等实例的相对位置不宜改变，所以选择稳定的归并排序。

6，比较排序总结

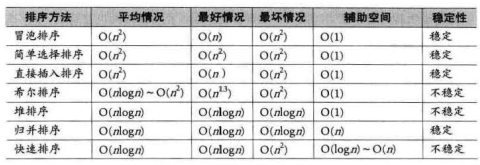
从算法的简单性来看，我们将 7 种算法分为两类:
• 简单算法:冒油、简单选择、直接插入。
• 改进算法:希尔、堆、归并、快速。

从平均情况来看，显然最后 3 种改进算法要胜过希尔排序，并远远胜过前 3 种简单算法。

从最好情况看，反而冒泡和直接插入排序要更胜一筹，也就是说，如果你的待排序序列总是基本有序，反而不应该考虑 4 种复杂的改进算法。

从最坏情况看，堆排序与归并排序叉强过快速排序以及其他简单排序。

参考：

《大话数据结构》

http://www.cnblogs.com/eniac12/p/5329396.html

posted @ 2018-06-07 17:18 xdyixia 阅读(423) 评论(0) 编辑收藏举报

刷新页面返回顶部