后量子密码（抗量子密码）

一、后量子密码是什么？

1.1，前言

　　后量子密码，作为未来 5-10 年逐渐代替 RSA、Diffie-Hellman、椭圆曲线等现行公钥密码算法的密码技术，正被越来越多的人所了解。目前，美国国家标准技术研究所 (NIST) 正在制定的新一代密码技术标准，正是后量子密码标准。

1.1.1，后量子密码是什么？

　　后量子密码是能够抵抗量子计算机对现有密码算法攻击的 新一代密码算法。

　　所谓“后”，是因为量子计算机的出现，现有的绝大多数公钥密码算法（RSA、Diffie-Hellman、椭圆曲线等）能被足够大和稳定的量子计算机攻破，所以可以抵抗这种攻击的密码算法可以在量子计算和其之后时代存活下来，所以被称为“后”量子密码。也有人称之为“抗量子密码”，说的都是一个意思。英文中的表述是："Post-quantum Cryptography (PQC)"，或者 "Quantum-resistant cryptography"。

1.1.2，为什么需要？

1）量子计算机很强大，但利用其强大算力的前提是：存在能高效解决问题的量子算法，否则量子计算机没什么用，反而因为其高昂的成本带来劣势。数据：5 量子比特的量子计算机造价在千万美元左右。

2）量子计算机现有的一些强大算法/应用包括：密码算法安全性、数学计算、机器学习等。

3）对于密码算法安全性，主要是针对公钥密码算法：

　　3.1）公钥密码算法安全性依赖的数学问题可以被高效的量子算法所解决。由于底层依赖的数学问题被解决，所以这些公钥密码算法不再安全。这些数学问题包括：离散对数 (及椭圆曲线版本)、大整数分解等。这直接影响目前使用的 RSA、Diffie-Hellman、椭圆曲线等算法。著名的量子算法是 1994 年的 Shor's algorithm。

　　3.2）关于对称密码算法和哈希函数（例如 AES、SHA1、SHA2 等），虽然有量子算法可以理论上攻破，但这个算法的影响有限，且有很多限制条件。著名的量子算法是 1996 年的 Grover's algorithm。

4）对于公钥密码算法，量子计算机对安全性的影响：

　　4.1）完全攻破目前广泛使用的公钥密码算法

　　4.2）增大参数的长度没有用。有人说：把 RSA 的长度从 1024 加到 2048 比特甚至更长，不就安全了吗？答案是：对于现有的经典计算机和算法，这样是可以的。但对于量子计算机和算法，这是徒劳的（除非 RSA 的长度增大到 1GB 或更长。但这样的话，算法还能用吗？对于其他算法呢？）

　　4.3）需要全新的公钥密码算法

5）对于对称密码算法，量子计算机对安全性的影响：

　　5.1）降低现有算法的安全性：安全性从 k-bit 降低为 k/2-bit

　　5.2）增大参数的长度有用

　　5.3）把密钥长度或哈希的长度加倍即可，例如：AES-128 升级至 AES-256，SHA-256 升级至 SHA-512 等。但这并不是必须的，原因后面会进行介绍

6）攻破 RSA-2048 的预计时间和开销：2030 年，量子计算机，10 亿美元，核电站 (PQCrypto 2014, Matteo Mariantoni 的预估)

关于量子计算机，再介绍几个结论：

（1）量子比特数量重要，但更重要的是质量。目前建造的量子计算机（例如 Google 的 72 qubit 芯片）中，qubit，也就是量子物理比特的质量很差。由于量子相干等物理机制，必须引入纠错机制，但需要成百上千个量子物理比特进行纠错，来实现一个量子逻辑比特的功能
（2）攻破现有的公钥密码算法需要几千甚至几万个逻辑比特。结合上面一点可以看到，建造量子计算机仍处在很初级的阶段
（3）D-Wave 建造的 D-Wave 2000Q “量子计算机” 实际上是量子退火算法的，并不是真正意义上的普遍适用的量子计算机
（4）对于量子算法（例如 Grover），需要指数级别的内存，因此 Grover 算法的威胁不如 Shor 的算法那么紧迫

用 NIST 后量子密码团队负责人 Dustin Moody 在 AsiaCrypt 2017 会议上的 Talk 概括一下：

可以看到：

（1）公钥密码算法：红色叉，需要后量子密码算法代替

（2）对称密码算法：蓝色框，不那么紧迫需要新算法代替。可以通过调整参数解决

1.1.3，我们需要什么样的？

显然，是后量子密码算法。更准确的说，是后量子密码技术标准。密码实践中的一个重要结论是：不要自己造轮子（除非你是大佬）。我们现在使用 RSA、Diffie-Hellman、椭圆曲线等算法正是在被定为国际标准后，才逐渐进入应用领域的。

后量子密码算法应该：

　　（1）安全：不仅要在现在的计算条件下安全，也要在量子计算机下安全

　　（2）运行速度快：现有的结果显示，相同安全强度下，后量子密码的计算速度可以超越现有公钥密码的计算速度

　　（3）通信开销合理：实践中几乎不会使用一个公钥/密文大小达到几 M 甚至更大的算法。目前的 RSA-2048 公钥大小约为 256 bytes，椭圆曲线大约为 64 bytes。最好的后量子密码算法的公钥大小在 1KB 左右

　　（4）可被用作现有算法和协议的直接代替，例如：公钥加密、密钥交换、数字签名等

　　（5）更广应用场景：例如：同态加密 (Homomorphic Encryption)、属性加密 (Attribute-based Encryption)、函数加密 (Functional Encryption)、不可区分混淆 (Indistinguishability Obfuscation) 等高级密码学应用

下图是 NIST 总结的后量子密码技术和应用栈：

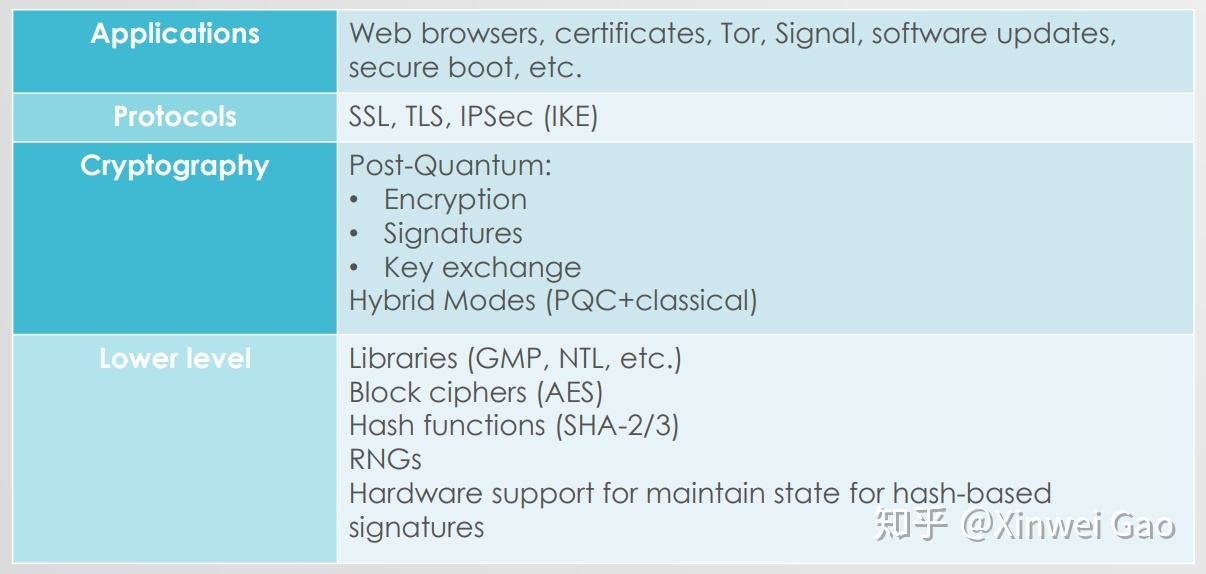
 1.1.4，什么时候需要？

这是不容易取得一致结论的地方，主要原因在于：

　　（1）对大型且稳定的量子计算机被建造出来的时间预估：未来 10 年左右

　　（2）新一代密码算法需要多久被确定，以及在真实世界中被应用

直观的结论是：我们要在现有密码算法被攻破前做好准备，尽管什么时间被攻破无人能给出准确的时间。做好准备是指，后量子算法从研究到真正被实际应用和部署，而非局限在学术界的研究领域。

值得注意的是，2015 年 8 月，美国国家安全局 (NSA) 呼吁迁移至可以抵抗量子计算机攻击的算法。有意思的是，作为破解加密通讯和密码算法的最大组织，NSA 站出来号召采用后量子密码算法。不知道他们是不是已经在现有的密码破解领域取得了极大的突破？

IAD will initiate a transition to quantum resistant algorithms in the not too distant future. Based on experience in deploying Suite B, we have determined to start planning and communicating early about the upcoming transition to quantum resistant algorithms." -- NSA

1.2，研究现状

1.2.1，概况

　　密码学界很早就在研究可以抵抗量子计算机攻击的密码算法，最早可以追溯到 1978/9 年的 McEliece 加密、 Merkle 哈希签名等。但在那时，量子计算机对密码算法的威胁并没有很明确，也没有“后量子”的概念。所以直到最近十几年，后量子密码的重要性逐渐显现出来。"Post-quantum" 的概念

对后量子密码技术的研究和标准制定有以下重要参与方：

　　（1）美国国家标准技术研究所 (NIST)。NIST 早在 2012 年启动了后量子密码的研究工作，并于 2016 年 2 月启动了全球范围内的后量子密码标准征集，并于 2017.11.30 截止草案提交。2018 年 4 月在 Florida 举办了第一届 PQC 标准化会议。NIST 预计在未来 5 年左右，确定新一代公钥密码算法标准

　　（2）欧盟：PQCRYPTO 项目

　　（3）欧洲电信标准化协会 (ETSI)：ETSI 也在寻求制定新一代后量子密码标准。ETSI 已举办了 6 届 workshop。2018 年的 workshop 将于 11 月在北京举行

　　（4）互联网工程任务组 (IETF)

　　（5）美国电气和电子工程师协会 (IEEE)

1.2.2，NIST 后量子密码标准征集

NIST PQC 标准征集工作与 2016 年正式启动。NIST 主要聚焦于以下 3 类后量子密码算法的征集：加密、密钥交换、数字签名。截至 2017.11.30 提交截止，NIST 共收到 82 个算法草案。在进行初步筛选后，NIST 公布了 69 个“完整且适合”的草案。

在 69 个候选草案中，主要包括以下 4 种数学方法构造的后量子密码算法：

  1. 格 (Lattice-based)
  2. 编码 (Code-based)
  3. 多变量 (Multivariate-based)
  4. 哈希 (Hash-based)

从 NIST 公布至今（2018.9），已经过去了近 1 年的时间。密码学界对这些算法进行了详细的密码分析，目前已有近 1/3 的算法被发现存在各种各样的缺陷，近 1/5 的算法已被彻底攻破。

1.3，应用现状

　　（1）最为著名的是 2016 年 Google 在 Chrome Canary 分支版本 (Chrome 54 beta) 中加入了基于 RLWE 问题的后量子密钥交换算法 NewHope。Google 在部分 Google 服务器上搭建了使用 NewHope + X25519 两种密钥交换算法构造的一个 TLS 密码套件 (Ciphersuite) CECPQ1 进行测试。测试进行了 2-3 个月后结束，并被移除出 Chrome

　　（2）微软研究院将其主推的后量子密码算法 Picnic 使用到 PKI 和 HSM 集群中

　　（3）微软研究院推出的后量子 VPN

　　（4）Open Quantum Safe (OQS) 将一些后量子密码算法与 TLS 结合，并开源了后量子 OpenSSL 库的测试实现

二、主要构造技术、对比和应用

2.1、概述

实现后量子密码算法主要有以下 4 种途径 ：

　　（1）基于哈希 (Hash-based)：最早出现于 1979 年，主要用于构造数字签名。代表算法：Merkle 哈希树签名、XMSS、Lamport 签名等

　　（2）基于编码 (Code-based)：最早出现于 1978 年，主要用于构造加密算法。代表算法：McEliece

　　（3）基于多变量 (Multivariate-based)：最早出现于 1988 年，主要用于构造数字签名、加密、密钥交换等。代表方法/算法：HFE (Hidden Field Equations)、Rainbow (Unbalanced Oil and Vinegar (UOV) 方法)、HFEv- 等

　　（4）基于格(Lattice-based)：最早出现于 1996 年，主要用于构造加密、数字签名、密钥交换，以及众多高级密码学应用，如：属性加密 (Attribute-based encryption)、陷门函数 (Trapdoor functions)、伪随机函数 (Pseudorandom functions)、同态加密 (Homomorphic Encryption) 等。代表算法：NTRU 系列、NewHope (Google 测试过的)、一系列同态加密算法 (BGV、GSW、FV 等)。由于其计算速度快、通信开销较小，且能被用于构造各类密码学算法和应用，因此被认为是最有希望的后量子密码技术

当参数选取适当时，目前没有已知的经典和量子算法可以快速求解这些问题。

再次强调，这些算法的安全性，依赖于有没有可以快速求解其底层数学问题或直接对算法本身的高效攻击算法。这也正是量子计算机对于公钥密码算法有很大威胁的原因。

除这 4 种问题之外，还有基于超奇异椭圆曲线 (Supersingular elliptic curve isogeny)、量子随机漫步 (Quantum walk) 等技术的后量子密码构造方法。另外，对称密码算法在密钥长度较大时 (例如 AES-256)，也可被认为是后量子安全的。

为什么上面列的 4 种是最重要的？

正如前面提到的，后量子密码主要的关注点在公钥密码上。这 4 类途径是最能构造出公钥密码学中已有的各类算法的后量子版本，甚至还能超越（例如基于格的(全)同态加密）等。

下面对 4 种主要构造后量子密码的技术进行介绍。

2.2， 四种构造后量子密码的途径

Note：由于每一种构造方法需要较深的数学和密码学知识，因此在本文中，我无法对细节做过多的介绍和描述。在介绍每种构造方法后，我会给出一些国外的专家们在会议上做的 talk 的 slide。这些 slide 对于入门非常有帮助。如果有兴趣，可以参考本文给出的链接进行进一步的了解和研究。

2.2.1 基于哈希 (Hash-based)

基于哈希的签名算法由 Ralph Merkel 提出，被认为是传统数字签名 (RSA、DSA、ECDSA 等 ) 的可行代替算法之一 [2]。基于哈希的签名算法由一次性签名方案演变而来，并使用 Merkle 的哈希树认证机制。哈希树的根是公钥，一次性的认证密钥是树中的叶子节点。基于哈希的签名算法的安全性依赖哈希函数的抗碰撞性。由于没有有效的量子算法能快速找到哈希函数的碰撞，因此（输出长度足够长的）基于哈希的构造可以抵抗量子计算机攻击。此外，基于哈希的数字签名算法的安全性不依赖某一个特定的哈希函数。即使目前使用的某些哈希函数被攻破，则可以用更安全的哈希函数直接代替被攻破的哈希函数。

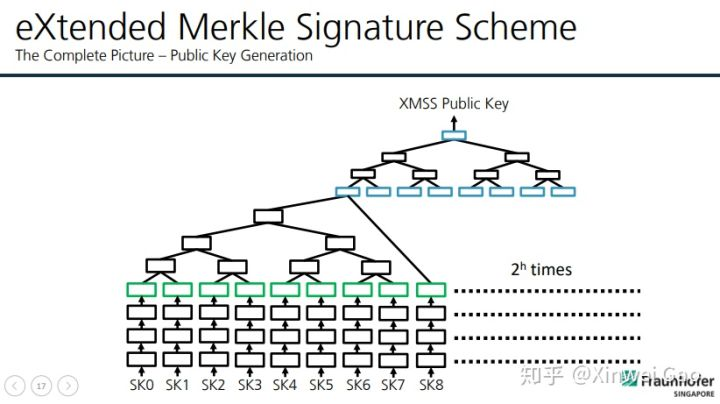
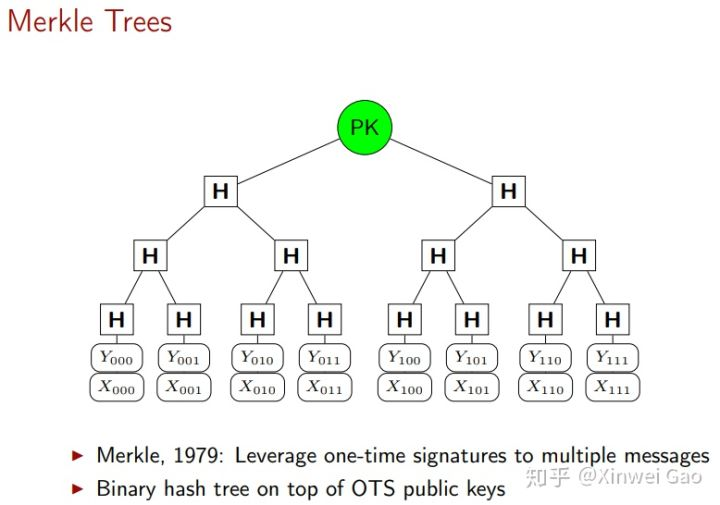
可参考的 slide：

https://www.fraunhofer.sg/content/dam/singapur/FWS/FWS01-PQC/slides/07_FWS01_XMSS.pdf

https://sphincs.cr.yp.to/slides-sphincs-20150428.pdf

2.2.2 基于编码 (Code-based)

基于编码的算法使用错误纠正码对加入的随机性错误进行纠正和计算。一个著名的基于编码的加密算法是 McEliece [3]。McEliece 使用随机二进制的不可约 Goppa 码作为私钥，公钥是对私钥进行变换后的一般线性码。Courtois、Finiasz 和Sendrier 使用 Niederreiter 公钥加密算法构造了基于编码的签名方案 [4]。基于编码的算法（例如 McEliece）的主要问题是公钥尺寸过大。基于编码的算法包括加密、密钥交换等。

 

 

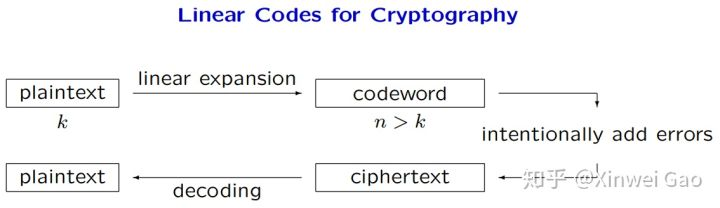
可参考的 slide：

https://2017.pqcrypto.org/exec/slides/cbctuto-ecrypt.pdf

https://pqcrypto2016.jp/data/Lange-20160223.pdf

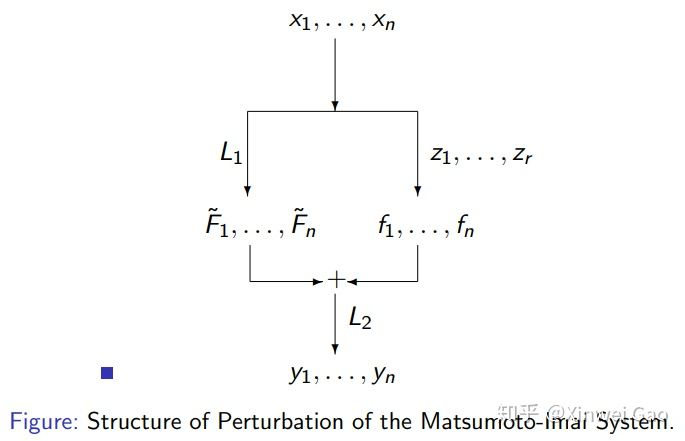
2.2.3 基于多变量 (Multivariate-based)

基于多变量的算法使用有限域上具有多个变量的二次多项式组构造加密、签名、密钥交换等算法 [5]。多变量密码的安全性依赖于求解非线性方程组的困难程度，即多变量二次多项式问题。该问题被证明为非确定性多项式时间困难。目前没有已知的经典和量子算法可以快速求解有限域上的多变量方程组。与经典的基于数论问题的密码算法相比，基于多变量的算法的计算速度快，但公钥尺寸较大，因此适用于无需频繁进行公钥传输的应用场景，例如物联网设备等。

 

 

 可参考的 slide：

https://2017.pqcrypto.org/school/slides/1-Basics.pdf

https://pqcrypto2016.jp/data/Ding-Fukuoka2016.pdf

https://web.stevens.edu/algebraic/Files/SCPQ/SCPQ-2011-02-02-talk-Ding.pdf

2.2.4 基于格 (Lattice-based)

基于格的算法由于在安全性、公私钥尺寸、计算速度上达到了更好的平衡，被认为是最有前景的后量子密码算法之一 [6]。与基于数论问题的密码算法构造相比，基于格的算法可以实现明显提升的计算速度、更高的安全强度和略微增加的通信开销 [7]。与其他几种实现后量子密码的方式相比，格密码的公私钥尺寸更小，并且安全性和计算速度等指标更优 [8]。此外，基于格的算法可以实现加密、数字签名、密钥交换、属性加密、函数加密、全同态加密等各类现有的密码学构造。基于格的算法的安全性依赖于求解格中问题的困难性。在达到相同（甚至更高）的安全强度时，基于格的算法的公私钥尺寸比上述三种构造更小，计算速度也更快，且能被用于构造多种密码学原语，因此更适用于真实世界中的应用。近年来，基于 LWE (Learning with Errors) 问题 [9] 和 RLWE (Ring-LWE) 问题 [10] 的格密码学构造发展迅速，被认为是最有希望被标准化的技术路线之一。

这里有一篇很好的入门和近 10 年格密码发展的 Survey：

https://web.eecs.umich.edu/~cpeikert/pubs/lattice-survey.pdf

 

 可参考的 slide：

https://www.math.uci.edu/~asilverb/Lattices/Slides/Daniele1uci13-handout.pdf

https://web.eecs.umich.edu/~cpeikert/pubs/slides-qcrypt.pdf

https://web.eecs.umich.edu/~cpeikert/pubs/slides-tcc09.pdf

http://www.ic.unicamp.br/ascrypto2013/slides/ascrypto2013_eduardomorais.pdf

https://www.cc.gatech.edu/fac/cpeikert/pubs/slides-suite.pdf

2.3，对比

下表中给出这 4 种后量子密码算法的粗略对比：

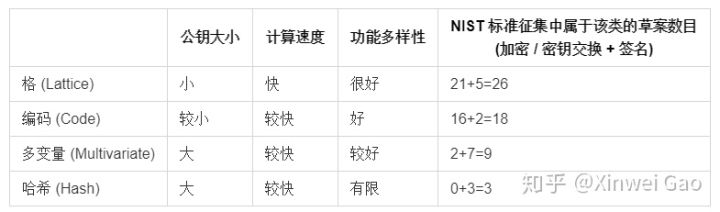
注意，表中的对比反应出该类后量子密码算法的平均性能指标，总体来说，趋势是基本吻合的。值得注意的是，一些算法具有极为突出的性能，并且可能与最快的后量子密码算法相接近。另外，由于编码和多变量密码在算法的功能上重叠的部分较少，因此不容易直接对比他们的性能。表中的对比结果仅供参考，具体的算法性能需要经过仔细的测试。

因此，在实际应用中具体采用哪个类别/哪个算法，需要针对应用场景进行详细分析。例如，在一些频繁需要交换公钥的场景（例如 HTTPS），可以使用 Lattice-based 的算法等。

2.4，应用场景

从 NIST 的后量子密码标准征集可以看到，NIST，作为美国国家标准技术研究所，最关心的是最基础且广泛应用的密码学算法：公钥加密、数字签名、密钥交换。现有的几十个提案，用 4 种不同的后量子密码实现方法，完成了这 3 个功能。因此，这些后量子密码算法中的佼佼者可以直接代替现有的公钥加密、数字签名、密钥交换算法，包括：RSA 加密/签名、Diffie-Hellman 密钥交换、椭圆曲线加密/签名等。

简单的讲：后量子密码算法能覆盖到的密码学原语/应用是至少不比现有的公钥密码算法少的。

与现有的公钥密码算法一样，后量子密码可以被应用于更高层次一些的协议/应用，包括：HTTPS (TLS)、数字证书 (PKI)、SSH、VPN、IPsec、比特币等数字货币、U 盾、桌面/移动操作系统等各个领域和应用中。现在用到公钥密码算法的应用，基本可以使用后量子密码算法进行代替。

此外，后量子密码还可以实现更高级的密码学应用，例如同态加密（基于格问题）等。

如果希望学习目前最好的加密、数字签名、密钥交换算法，推荐从 NIST 后量子密码标准征集算法选择一些进行研究。

https://csrc.nist.gov/Projects/post-quantum-cryptography/round-2-submissions

三、美国国家标准技术研究所（NIST）新一代公钥密码算法标准征集

美国国家标准技术研究所（National Institute of Standards and Technology，NIST）的前身为国家标准局，属于美国商务部。NIST 为产业界、学术界、政府及其他用户提供了超过 1300 种标准参考材料。NIST 最主要的职责是建立美国国家的一系列标准和基准。除此之外，NIST 还有一系列权威的算法检测和竞赛，例如 NIST 的人脸识别算法测试。

3.1 NIST 指定的密码学算法标准/规范

在密码学领域，NIST 确立了一系列标准算法和规范。目前广泛使用的一系列算法和标准，很大一部分都是 NIST 指定的，包括且不仅限于以下内容：

3.2 NIST 后量子密码算法征集

NIST 的后量子密码项目主页：

3.3 主要内容

NIST 的后量子密码算法标准征集竞赛共征集两类公钥密码算法：

  • 公钥加密（密钥交换）
  • 数字签名

NIST 要求每个团队提交可以抵抗量子计算机攻击的算法详细文档、工程实现和测试向量数据。此次后量子密码算法标准征集竞赛面向全球范围展开，共有来自 6 个大洲，25 个国家和地区的密码学家参与了竞赛，最终 NIST 选择了 69 个提案进入第一轮筛选。

NIST 对于算法的选择标准大致是：

  • 安全性：算法对于经典计算机和量子计算机下攻击的复杂度
  • 性能：与目前的公钥密码算法速度进行对比 - 特性：算法与现有互联网协议/应用的兼容度、前向安全、抵抗侧信道攻击、灵活性等等

对于安全性，NIST 要求提交的算法提供的参数至少达到 AES-128 的安全性，达到 AES-192 和 AES-256 的安全性更佳。

对于后量子密码算法标准化，NIST 主要面临以下复杂问题：

  • 更广的范围：同时制定公钥加密、密钥交换和数字签名算法
  • 在经典/量子计算机的攻击下，算法的安全性评估：CPA/CCA；经典/量子计算机攻击复杂度；安全性证明；其他 Cryptanalysis 结果
  • 理论安全模型和实际攻击的 gap
  • 安全性、性能、公约大小、签名长度、侧信道攻击等各个方面间的 tradeoff
  • 应用至现有和新的安全应用中的困难程度，例如 TLS、IKE、PKI 等

 

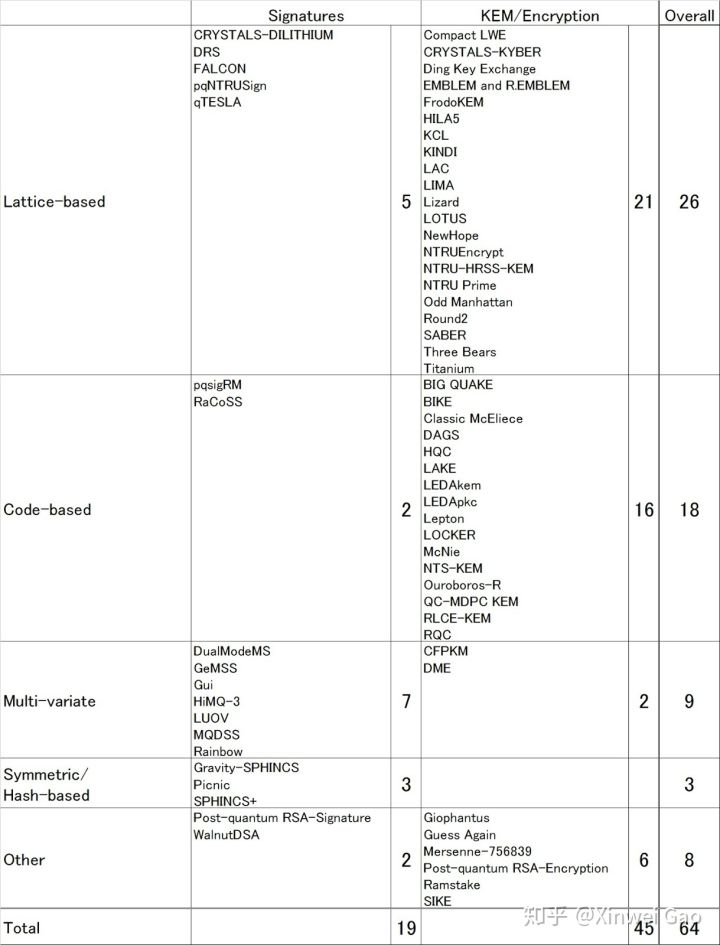
上图引用了 Ryo Fujita 统计的 NIST 后量子密码算法标准征集第一轮的各个算法、所属分类及每一类原语的候选算法个数，包括基于格、编码、多变量、哈希和其他方法构造的后量子密码算法。可以看到：

  • 基于格和编码的构造是最多的，且主要被用于构造公钥加密（密钥交换）算法
  • 由于基于多变量的陷门构造相对更为可行和高效，因此基于多变量的构造主要集中于数字签名方案，公钥加密方案较少
  • 由于基于哈希的构造方案中树状结构的使用，因此目前只有数字签名的构造，缺少公钥加密算法

还有一些方案没有被归类于经典的 4 种后量子密码算法构造中。这些方案使用了不同于格、编码、多变量、哈希的困难问题进行构造，例如 Post-quantum RSA 加密和签名使用了尺寸极大的 RSA 模数（公钥大小接近几百 MB 甚至 GB 级别）， SIKE 使用了超奇异椭圆曲线等。图中还有 3 个由于已被彻底攻破而主动撤回的方案。总体来看，基于格的方案数量最多，公钥加密（密钥交换）的方案数量比数字签名方案数量更多。

与 2015 年正式结束的 SHA-3 哈希函数标准化竞赛相比，NIST 的后量子密码算法标准征集工作有以下区别：

  • 后量子密码的标准化和研究比新一代哈希函数 SHA-3 的标准化复杂得多，主要在于各类实现后量子密码的技术和算法有各自的特点，不容易选择唯一的一个算法；另外，对于后量子密码和量子计算的研究尚不足够透彻，因此对安全性分析和标准制定有影响
  • NIST 预计选择几个较优的算法，而不是指定唯一一个赢家
  • 对于算法的衡量标准可能随着新的研究结果的出现而改变

由于 NIST 的后量子密码标准征集工作具有很大的影响力，密码学界对于这项工作关注度很高。下图给出了 Tanja Lange 总结的已被攻破/有问题的算法，其中红色的是被彻底攻破的算法，深黄色的是需要大改才能保证安全性的算法：

 

 比较有趣的是，在 NIST 公布所有算法的提案后的几个小时内，就有一个算法被彻底攻破而被迫撤回。在随后的几天内，同一位密码学家又发布了一系列针对不同算法的攻击方法，导致几个算法早早被淘汰。

3.4 国内参与情况

国内参加到 NIST 的后量子密码标准征集工作中的团队主要有：

    • 密码科学技术国家重点实验室的 Jiang Zhang
    • 上海交大的 Yu yu
    • 复旦大学的 Yunlei Zhao
    • 中科院信工所的 Xianhui Lu 团队
    • 台湾中央研究院的 Bo-Yin Yang 和 Ming-Shing Chen

共覆盖 5 个提案左右。此外，还有一些就职于国外院校/机构的中国/华裔学者。

3.5 时间线

3.6 其他标准化组织的行动

  • IEEE P1363.3 中已标准化基于格的密码算法：
  • IETF 在 RFC 8391 中标准化 XMSS，一个有状态的基于哈希的签名算法：
  • ETSI 也在寻求制定新一代后量子密码标准。目前 ETSI 已举办了 6 届 workshop。2018 年的 workshop 将于 11 月在北京举行
  • 欧洲的 PQCrypto 和 SafeCrypto 发布了数个针对后量子密码的初步标准化建议和研究报告
  • ISO/IEC JTC 1 SC27 已开展对后量子密码的研究

 

转自：知乎  Xinwei Gao    https://zhuanlan.zhihu.com/p/45393166

posted @ 2019-09-30 11:08  xdyixia  阅读(26654)  评论(1)  编辑  收藏  举报