同态加密

一：什么是同态加密（Homomorphic Encryption）

Craig Gentry给出的直观定义：

A way to delegate processing of your data, without giving away access to it.

    　一般的加密方案关注的都是数据存储安全。没有密钥的用户，不可能从加密结果中得到有关原始数据的任何信息。我们注意到，这个过程中用户是不能对加密结果做任何操作的，只能进行存储、传输。对加密结果做任何操作，都将会导致错误的解密，甚至解密失败。

        同态加密方案最有趣的地方在于，其关注的是数据处理安全。同态加密提供了一种对加密数据进行处理的功能。也就是说，其他人可以对加密数据进行处理，但是处理过程不会泄露任何原始内容。同时，拥有密钥的用户对处理过的数据进行解密后，得到的正好是处理后的结果。

二：同态加密有什么用处？

        同态加密几乎就是为云计算而量身打造的！我们考虑下面的情景：一个用户想要处理一个数据，但是他的计算机计算能力较弱。这个用户可以使用云计算的概念，让云来帮助他进行处理而得到结果。但是如果直接将数据交给云，无法保证安全性啊！于是，他可以使用同态加密，然后让云来对加密数据进行直接处理，并将处理结果返回给他。这样一来：

• 用户向云服务商付款，得到了处理的结果；
• 云服务商挣到了费用，并在不知道用户数据的前提下正确处理了数据；

       但是，这么好的特性肯定会带来一些缺点。同态加密现在最需要解决的问题在于：效率。效率一词包含两个方面，一个是加密数据的处理速度，一个是这个加密方案的数据存储量。

业界如何评价全同态加密的构造？在此引用一个前辈的话：

如果未来真的做出了Practical Fully Homomorphic Encryption，那么Gentry一定可以得到图灵奖。

（第一个构造出全同态加密方案的人是Gentry）

 三：同态加密具体如何定义？

 我们在云计算应用场景下面进行介绍：

 

 

 

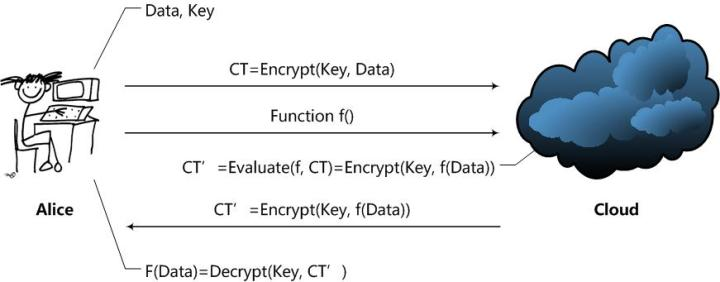
Alice通过Cloud，以Homomorphic Encryption（以下简称HE）处理数据的整个处理过程大致是这样的：

1. Alice对数据进行加密。并把加密后的数据发送给Cloud；
2. Alice向Cloud提交数据的处理方法，这里用函数f来表示；
3. Cloud在函数f下对数据进行处理，并且将处理后的结果发送给Alice；
4. Alice对数据进行解密，得到结果。

据此，我们可以很直观的得到一个HE方案应该拥有的函数：

• KeyGen函数：密钥生成函数。这个函数应该由Alice运行，用于产生加密数据Data所用的密钥Key。当然了，应该还有一些公开常数PP（Public Parameter）；
• Encrypt函数：加密函数。这个函数也应该由Alice运行，用Key对用户数据Data进行加密，得到密文CT（Ciphertext）；
• Evaluate函数：评估函数。这个函数由Cloud运行，在用户给定的数据处理方法f下，对密文进行操作，使得结果相当于用户用密钥Key对f(Data)进行加密。
• Decrypt函数：解密函数。这个函数由Alice运行，用于得到Cloud处理的结果f(Data)。

那么，f应该是什么样子的呢？HE方案是支持任意的数据处理方法f？还是说只支持满足一定条件的f呢？根据f的限制条件不同，HE方案实际上分为了两类：

• Fully Homomorphic Encryption (FHE)：这意味着HE方案支持任意给定的f函数，只要这个f函数可以通过算法描述，用计算机实现。显然，FHE方案是一个非常棒的方案，但是计算开销极大，暂时还无法在实际中使用。
• Somewhat Homomorphic Encryption (SWHE)：这意味着HE方案只支持一些特定的f函数。SWHE方案稍弱，但也意味着开销会变得较小，容易实现，现在已经可以在实际中使用。

四：什么叫做安全的HE？

        HE方案的最基本安全性是语义安全性（Semantic Security）。直观地说，就是密文（Ciphertext）不泄露明文（Plaintext）中的任意信息。如果用公式表述的话，为：

        

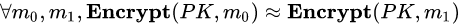
        这里PK代表公钥（Public Key），是非对称加密体制中可以公开的一个量。公式中的"约等于"符号，意味着多项式不可区分性，即不存在高效的算法，可以区分两个结果，即使已知m0, m1和PK。有人说了，这怎么可能？我已经知道m0, m1了，我看到加密结果后，对m0或者m1在执行一次加密算法，然后看哪个结果和给定结果相同不就完了？注意了，加密算法中还用到一个很重要的量：随机数。也就是说，对于同样的明文m进行加密，得到的结果都不一样，即一个明文可以对应多个密文（many ciphertexts per plaintext）。

        在密码学中，还有更强的安全性定义，叫做选择密文安全性（Chosen Ciphertext Security）。选择密文安全性分为非适应性（None-Adaptively）和适应性（Adaptively），也就是CCA1和CCA2。
        知乎er一大坨的答案中已经间接提到了，HE方案是不可能做到CCA2安全的。那么，HE方案能不能做到CCA1安全呢？至今还没有CCA1安全的FHE方案，但是在2010年，密码学家们就已经构造出了CCA1的SWHE方案了

五：举个SWHE的例子？

        在2009年Graig Gentry给出FHE的构造前，很多加密方案都具有Somewhat Homomorphism的性质。实际上，最最经典的RSA加密，其本身对于乘法运算就具有同态性。Elgamal加密方案同样对乘法具有同态性。Paillier在1999年提出的加密方案也具有同态性，而且是可证明安全的加密方案哦！后面还有很多啦，比如Boneh-Goh-Nissim方案, Ishai-Paskin方案等等。不过呢，2009年前的HE方案要不只具有加同态性，要不只具有乘同态性，但是不能同时具有加同态和乘同态。这种同态性用处就不大了，只能作为一个性质，这类方案的同态性一般也不会在实际中使用的。

 

在此我们看一下Elgamal加密方案，看看怎么个具有乘同态特性。Elgamal加密方案的密文形式为： 

 

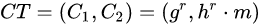
其中r是加密过程中选的一个随机数，g是一个生成元，h是公钥。如果我们有两个密文：     

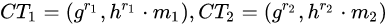
 我们把这两个密文的第一部分相乘，第二部分相乘，会得到：

 

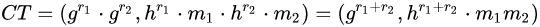
也就是说，m1的密文m2的密文相乘得到的的密文正好是m1m2所对应的密文。这样，用户解密后得到的就是m1m2的结果了。而且注意，整个运算过程只涉及到密文和公钥，运算过程不需要知道m1m2的确切值。所以我们说Elgamal具有乘同态性质。但是很遗憾，其没有加同态性质。

 

例：加密函数E，明文x，y

加法同态，如果存在有效算法⊕，E(x+y)=E(x)⊕E(y)或者 x+y=D(E(x)⊕E(y))成立，并且不泄漏 x 和 y。

乘法同态，如果存在有效算法 ，E(x×y)=E(x) E(y)或者 xy=D(E(x) E(y))成立，并且不泄漏 x 和 y。

内容来自：https://www.zhihu.com/question/27645858

https://baike.baidu.com/item/%E5%90%8C%E6%80%81%E5%8A%A0%E5%AF%86/6380351