POJ 2826 An Easy Problem!?(超级恶心!!!···)
题目:POJ2826
这道题WA了无数次啊。。。惨不忍睹,到现在实在找不到错了。。T_T
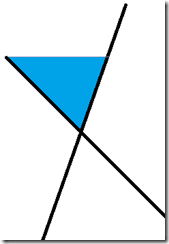
题目大意:两块木板,随意摆放,有雨水垂直落下到两块木板所形成的空间中,求能盛多少雨水(面积)。如图:
那么能盛放的雨水便是蓝色部分的面积。看起来很简单···实际上要考虑的情况很多啊!能1A的人都是神呐!
大概有以下几种要特别注意的情况:
1.有其中一个木板与地面平行,输出0
2.两个木板平行,输出0
3.两个木板重合相交(平行),输出0
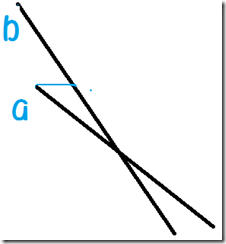
4.这个容易出错,就是当某木板挡住下面木板的时候,如图:
这样也输出0.
上面4种情况中第四种的判断比较麻烦,我是先确定两个木板各自靠上的顶点a,b。比较出较低的那个顶点,假如为a。那么做一条过a的与地面平行的直线,求出与另一条直线的交点,判断交点和点a的位置关系,即两条直线的“左右”关系,之后再判断b点是否遮挡住a点就很简单了,即假如本来属于右边木板的b点却在a点的左边,那么输出0。
除了这四种情况,就是求面积了。具体还是要作与a点平行的直线,求出交点c,然后结合两个木板的交点用叉积求面积就可以了。
一开始我没考虑第一种情况,wa了几次。
后来发现精度问题有wa了几次。
后来第四种情况的处理又出现了一些头疼的问题再后来看了看discuss把注意的有改了改...
再后来下了网上提供的10W个测试数据,过了。。。结果还是一直WA啊!
跪了。。不想看了。这道题确实恶心,不过也确实能锻炼查错能力=。=以后再说吧,先不管了。。![]()
我的错误代码:
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cstdlib> 5 #include<cmath> 6 #define eps 1e-8 7 #define MAXX 100000 8 #define max(a,b) (a) > (b) ? (a) : (b) 9 #define min(a,b) (a) < (b) ? (a) : (b) 10 using namespace std; 11 12 struct point{ 13 double x,y; 14 point() {} 15 point(double x,double y) : x(x),y(y) {} 16 }p[5]; 17 18 int dcmp(double x){ 19 if(fabs(x) < eps) return 0; 20 if(x > eps) return 1; 21 return -1; 22 } 23 24 double cross(point p0, point p1, point p2){ 25 return ( p1.x - p0.x )*( p2.y - p0.y )-( p2.x - p0.x )*( p1.y - p0.y ); 26 } 27 28 point intersection(point u1,point u2,point v1,point v2){ 29 point ret=u1; 30 double t=((u1.x-v1.x)*(v1.y-v2.y)-(u1.y-v1.y)*(v1.x-v2.x)) 31 /((u1.x-u2.x)*(v1.y-v2.y)-(u1.y-u2.y)*(v1.x-v2.x)); 32 ret.x+=(u2.x-u1.x)*t; 33 ret.y+=(u2.y-u1.y)*t; 34 return ret; 35 } 36 37 bool isIntersected(point s1,point e1, point s2,point e2){ //一定要 + eps 。。。 38 return (max(s1.x,e1.x) >= min(s2.x,e2.x) + eps) && 39 (max(s2.x,e2.x) >= min(s1.x,e1.x) + eps) && 40 (max(s1.y,e1.y) >= min(s2.y,e2.y) + eps) && 41 (max(s2.y,e2.y) >= min(s1.y,e1.y) + eps) && 42 (cross(s1,s2,e1)*cross(s1,e1,e2) >= 0) && 43 (cross(s2,s1,e2)*cross(s2,e2,e1) >= 0); 44 } 45 46 double solve(){ 47 point p0,temp1,temp2; 48 p0 = intersection(p[1],p[2],p[3],p[4]); 49 // cout<<p0.x<<" * * "<<p0.y<<endl; 50 point ans1,ans2; 51 int tt1,tt2; 52 if(p[1].y > p[2].y) {ans1 = p[1];tt1 = 2;} 53 else {ans1 = p[2]; tt1 = 1;} 54 if(p[3].y > p[4].y) {ans2 = p[3];tt2 = 4;} 55 else {ans2 = p[4]; tt2 = 3;} 56 if(ans1.y >= ans2.y ){ 57 temp1 = point(MAXX,ans2.y); 58 temp2 = intersection(ans2,temp1,ans1,p[tt1]); 59 // cout<<temp2.x<<" * * "<<temp2.y<<endl; 60 if(temp2.x > ans2.x){ 61 if(dcmp(ans2.x-ans1.x) >= 0) return 0.0; 62 else 63 if(dcmp(ans1.x-ans2.x) >= 0) return 0.0; 64 } 65 double area = cross(temp2,ans2,p0)/2.0; 66 // cout<<"^&*^*& "<<cross(temp2,ans2,p0)<<endl; 67 return fabs(area); 68 } 69 70 if(ans1.y < ans2.y){ 71 point tem = ans2; 72 ans2 = ans1; 73 ans1 = tem; 74 temp1 = point(MAXX,ans2.y); 75 temp2 = intersection(ans2,temp1,ans1,p[tt1]); 76 if(temp2.x > ans2.x) { 77 if(dcmp(ans2.x-ans1.x) >= 0) return 0.0; 78 else 79 if(dcmp(ans1.x-ans2.x) >= 0) return 0.0; 80 } 81 double area = cross(temp2,ans2,p0)/2.0; 82 return fabs(area); 83 } 84 } 85 86 87 int main(){ 88 int t; 89 freopen("1.txt","r",stdout); 90 scanf("%d",&t); 91 while(t--){ 92 for(int i = 1;i <= 4;i++) 93 scanf("%lf%lf",&p[i].x,&p[i].y); 94 if(dcmp((p[2].y - p[1].y) * (p[4].x - p[3].x) - (p[4].y - p[3].y) * (p[2].x - p[1].x)) == 0) //平行 95 {puts("0.00"); continue;} 96 if(!isIntersected(p[1],p[2],p[3],p[4])) { puts("0.00"); continue;} 97 double ans = solve(); 98 printf("%.2f\n",ans + eps); 99 } 100 // system("pause"); 101 return 0; 102 }