线段树（ 进阶 ）

线段树

蓝某杯省赛比赛结束后，倒数第二题是线段树，但是我没想到怎么建树。时隔几个月，蓝某杯国赛结束后，这题线段树可以做，但是我没写出来。（这是我一个朋友[doge]）

简介

​ 线段树作为一个高级数据结构，而且是高级数据结构里面比较简单的一种，蓝某杯最喜欢拿他做压轴题。而压轴题的分一般都是20~25分，所以做出来 = 拿奖。相信你已经迫不及待想知道这个让算法大佬都又爱又恨的数据结构长什么样了吧。

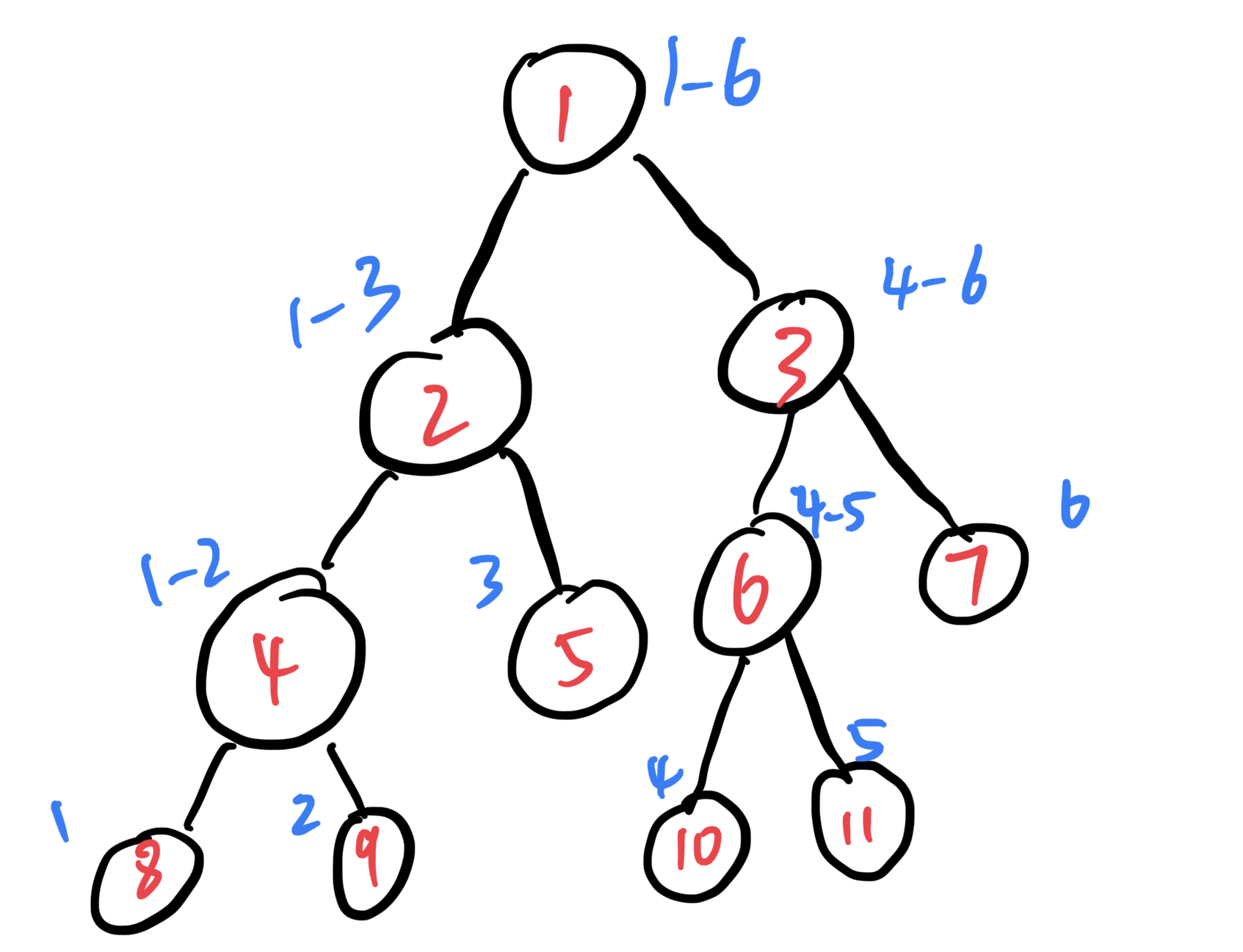
1. 线段树是一颗二叉搜索树，一个结点储存的信息是一个区间的信息，一般用一维数组来表示线段树。
2. 每个父结点有两个子节点，将父节点的区间成两个区间（一般都是从中间分），子节点分别存储这两个区间的数据。
3. 叶子节点的区间大小为1，存储的是单个数据。
4. 线段树的查询复杂度是O(logn)，空间复杂度为O(n<<3) = O(8*n) ≈ O(n)，适合处理频繁区间查询的任务。

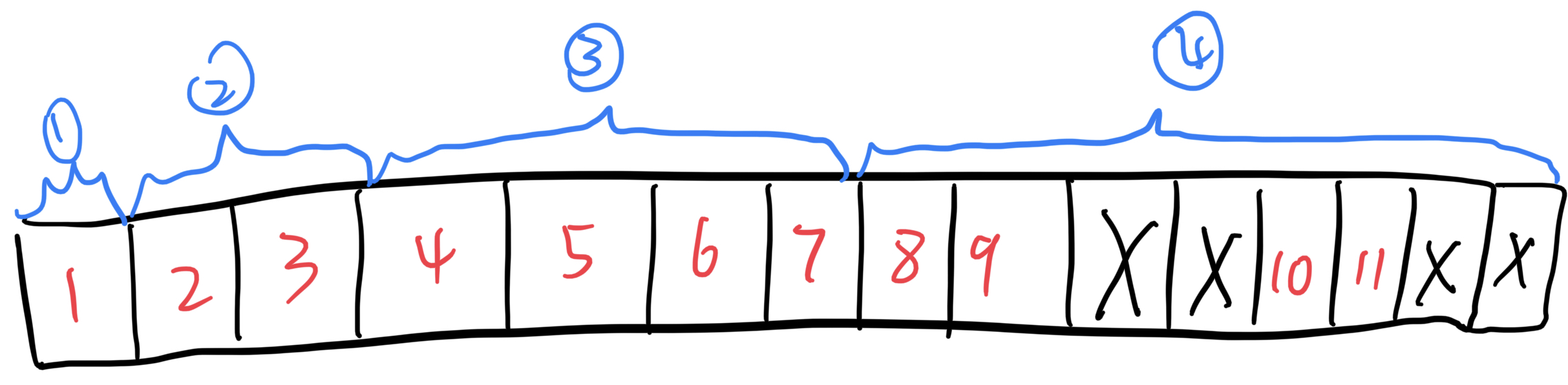
​ 假设有个长度为8的数组。不难理解，结点8~15 存储的是这个数组的元素。那么结点1~7 存储的是什么呢？这1~7 存储什么根据你的需求来定，你可以存储这个区间的最大值、最小值、区间和……

代码实现

下面以存储区间和来建一个线段树。

获得子树索引

设某结点某结点在数组中索引为i，结点的左右子树的索引分别为 2*i 和 2*i+1。可以自行带一下公式验证一下。

long long ls(long long x) { return x<<1; } // << 左移运算符，相当于*2
long long rs(long long x) { return x<<1|1; } // | 按位或运算，可以理解为+1，

建树

/**
 * 建树是一个递归的过程，从根节点开始。 build(1,1,n);
 * p: 当前的结点索引
 * pl: 当前节点区间左端 （point left）
 * pr: 当前节点区间右端 （point right）
 */
void build(long long p,long long pl,long long pr)
{
    tag[p] = 0;
    // 长度为1的结点，最底层 
    if(pl == pr) 
    {
        tree[p] = arr[pl];
        return ;
    }
    // 分治
    long long mid = pl + pr >> 1;
    build(ls(p),pl,mid);
    build(rs(p),mid+1,pr);
    // 合并结果
    tree[p] = tree[ls(p)] + tree[rs(p)];
}

修改

当你如果你只需要修改单个数据 ，直接修改的时间复杂度为 O(1)，那你完全不需要用线段树。但是如果你需要频繁的对你的数组某一区间的所有结点进行修改，直接一个一个修改的时间复杂度为 O(n)，那么线段树就是一个不错的数据结构，因为他可以在 O(logn) 的复杂度完成这个区间修改的行为。

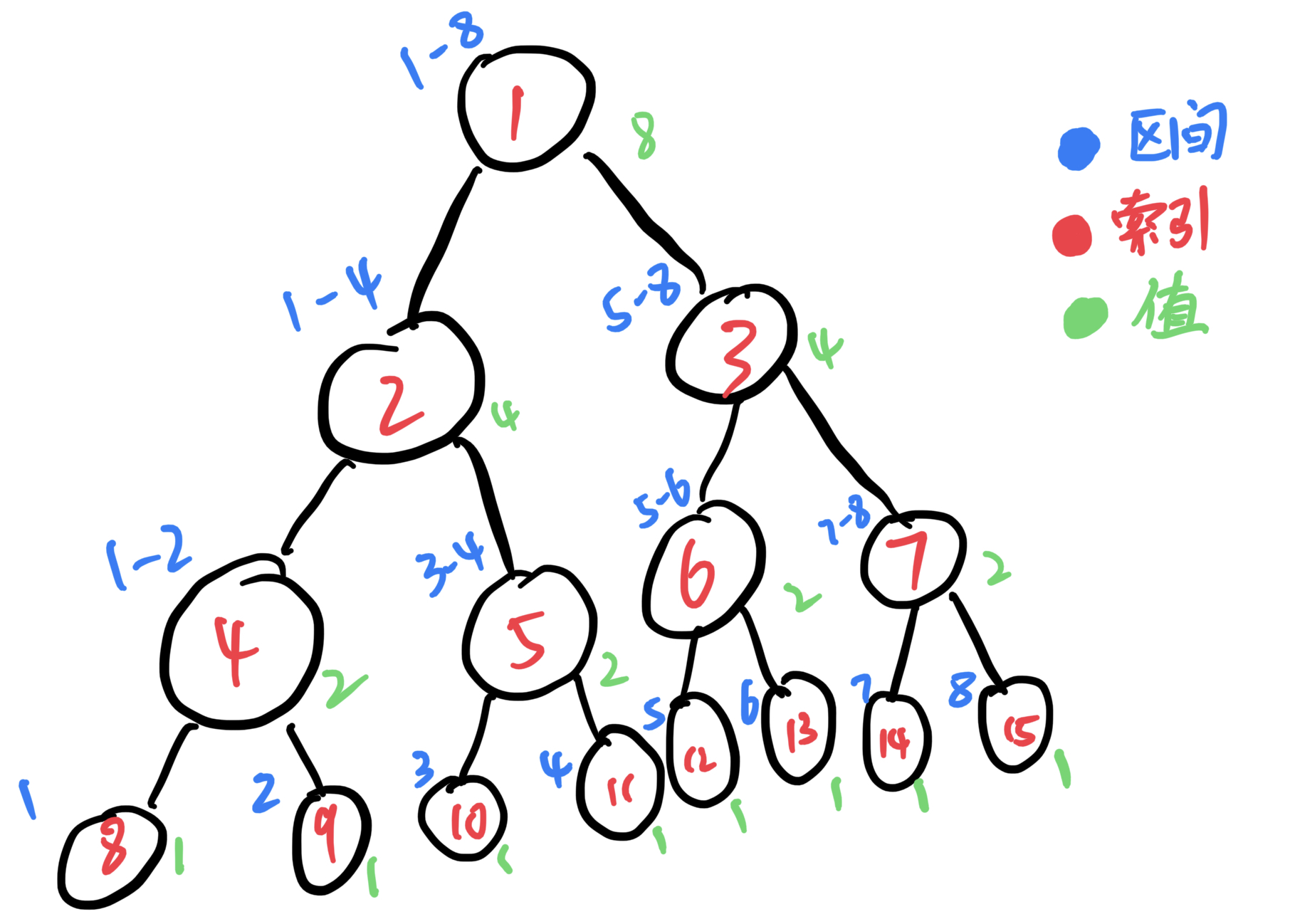
那么我们来讲线段树的区间修改，用长度为8，所有值为1的数组来建树可得下图。假如我们要让区间2~4 中每个结点的值都加d（假设d = 1）。那我们看着图来模拟一下，首先我们要让结点8、9、10、11和12的值加d。因为父节点的值是两个子节点的和，子节点如果被改变了，那我们就要把这个改变传递到父节点，就有了：结点4和5的值加2*d，2的值加4*d，6、3的值加d，1的值加5*d。

/**
 * 区间修改是一个递归的过程，从根节点开始往下
 * 然后将结果从下往上合并。 update(2, 4, 1, 1, n, k);
 * L: 要修改区间的左端点
 * R: 要修改区间的右端点
 * p: 当前的结点索引
 * pl: 当前节点区间左端 （point left）
 * pr: 当前节点区间右端 （point right）
 * d: 要修改区间的每个节点加d
 */
void update(long long L,long long R,long long p,long long pl,long long pr,long long d)
{
    // 区间为1的结点（叶子节点）
    if(pl==pr)
    {
        tree[p] += d;
        return;
    }
    // 区间大小不为1，则继续往下更新
    long long mid = pl + pr >> 1;
    if(L<=mid) update(L,R,ls(p),pl,mid,d);
    if(mid<R) update(L,R,rs(p),mid+1,pr,d);
    // 递归的过程中，子节点的值已经更新
    // 根据两个子节点重新计算父节点的值
    tree[p] = tree[ls(p)] + tree[rs(p)];
}

好的，区间的修改讲完了（bushi

假设区间中的每个值都加d，计算一下上面的代码的时间复杂度，你会发现修改一次的时间复杂度达到了恐怖的 O(nlogn)，并没有到达我们预期的 O(logn)。但是别人都说区间修改的复杂度为 O(logn) 呀，到底哪里出了问题？

别急上面的那些代码只是为了让你更好的理解线段树的精髓 —— lazy tag。lazy tag又称懒标记，详细的说就是，通过一个标记让计算机偷懒，从而少进行一些更新，从而降低时间复杂度。引入懒标记的线段树，区间修改的时间复杂度是 O(logn)，lazy tag的形状和tree的形状一样，每个tag标记一个节点。

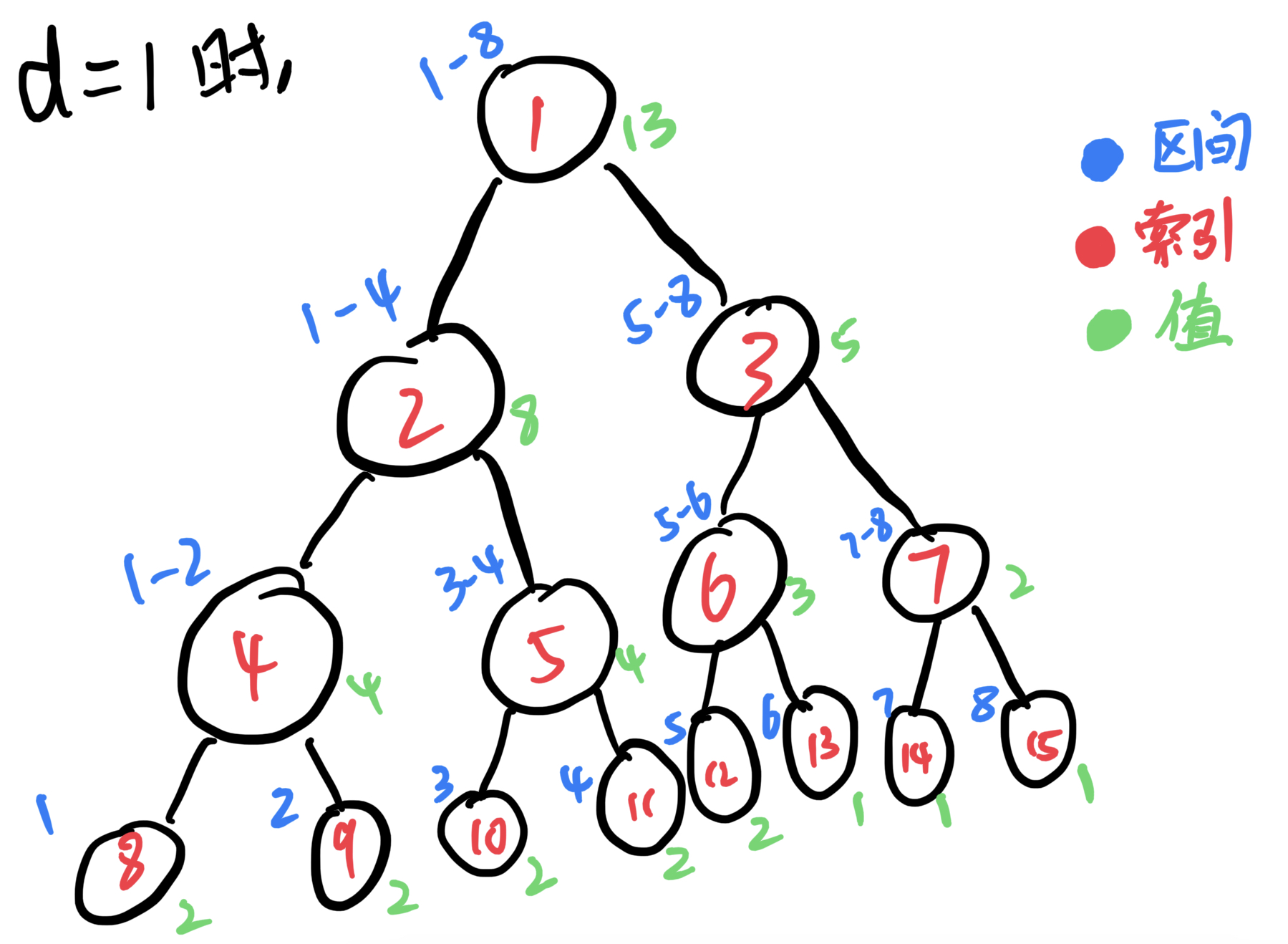
那么怎么样可以让计算机来偷懒呢？当进行区间修改的时候，如果结点所表示的区间被要修改的区间完全覆盖，可以将要修改的值——d，累加到lazy tag中，不进行向下的传递。当某一轮的要修改或者要查询的区间与当前节点的区间有交集但是不是覆盖关系的时候再向下传递。晕不晕？没关系，我们继续来模拟，还是刚才的例子。节点2表示了区间1~4，被要修改的区间1~5完全覆盖，那我们可以给结点2的lazy tag加d，代表结点2所表示区间中的每一个值都要加d。

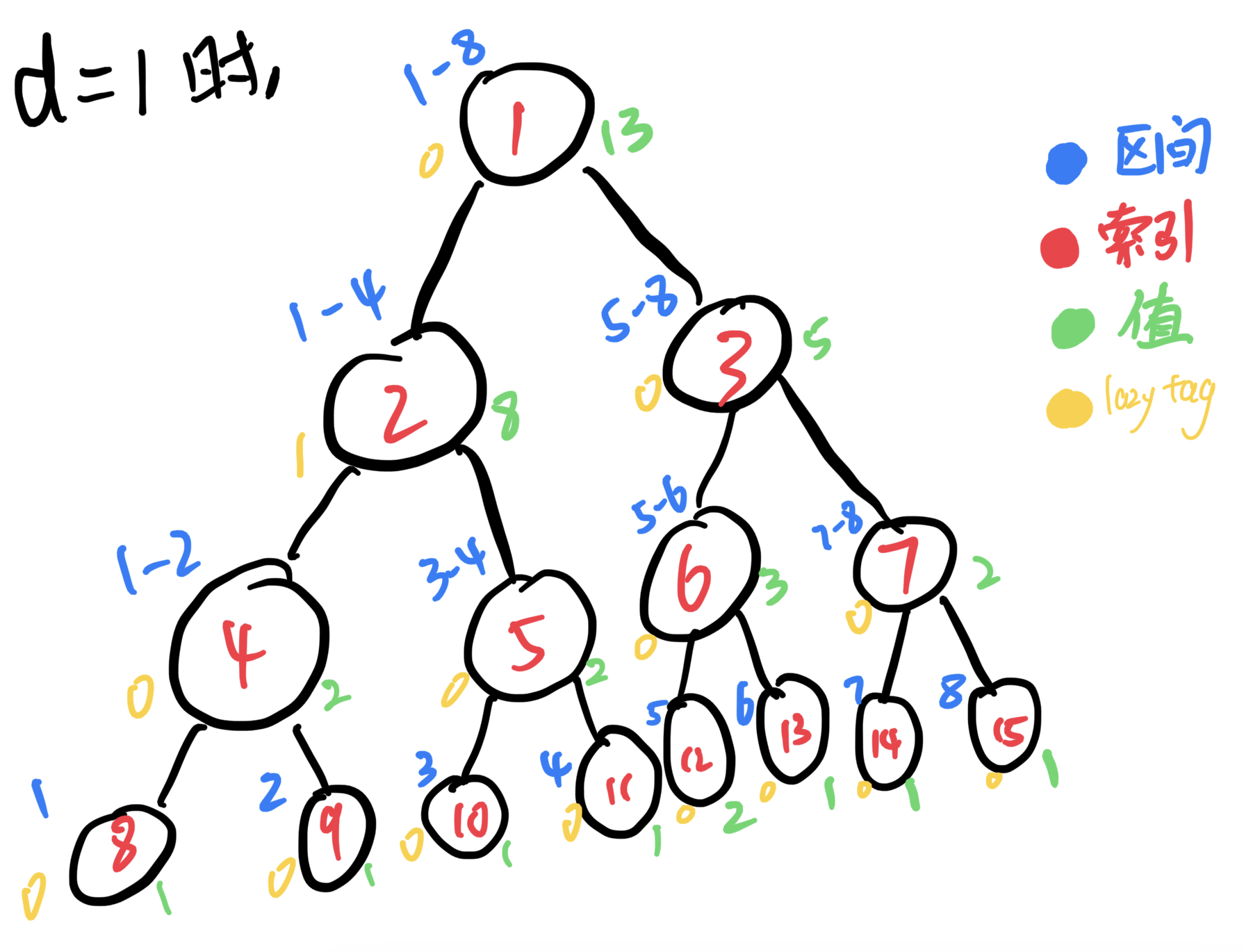
如上图所见，结点2的lazy tag值为1，且结点2的所有子节点和孙子节点都没有进行更新，因为没有必要进行更新，我们这个时候不需要知道子节点和孙子节点的值，而要更新的值我们已经存在lazytag中，以后需要知道子节点或孙子节点的值时，再进行向下传递就可以了，这就是线段树的精髓 lazy tag。

接下来来模拟一下向下传递的过程，接着上面继续进行修改，这次我只要修改结点4（记做区间4~4）的值，区间4~4中的每个值加d。区间4~4没办法覆盖结点2所表示的区间1~4且他们之间有交集，这时候就需要向下传递了。结点2的lazytag传给结点4和5的lazytag。区间4~4也无法覆盖结点5所表示的区间3~4，继续向下传递。这时候传递完了，再向上更新，这一轮的修改就结束了。

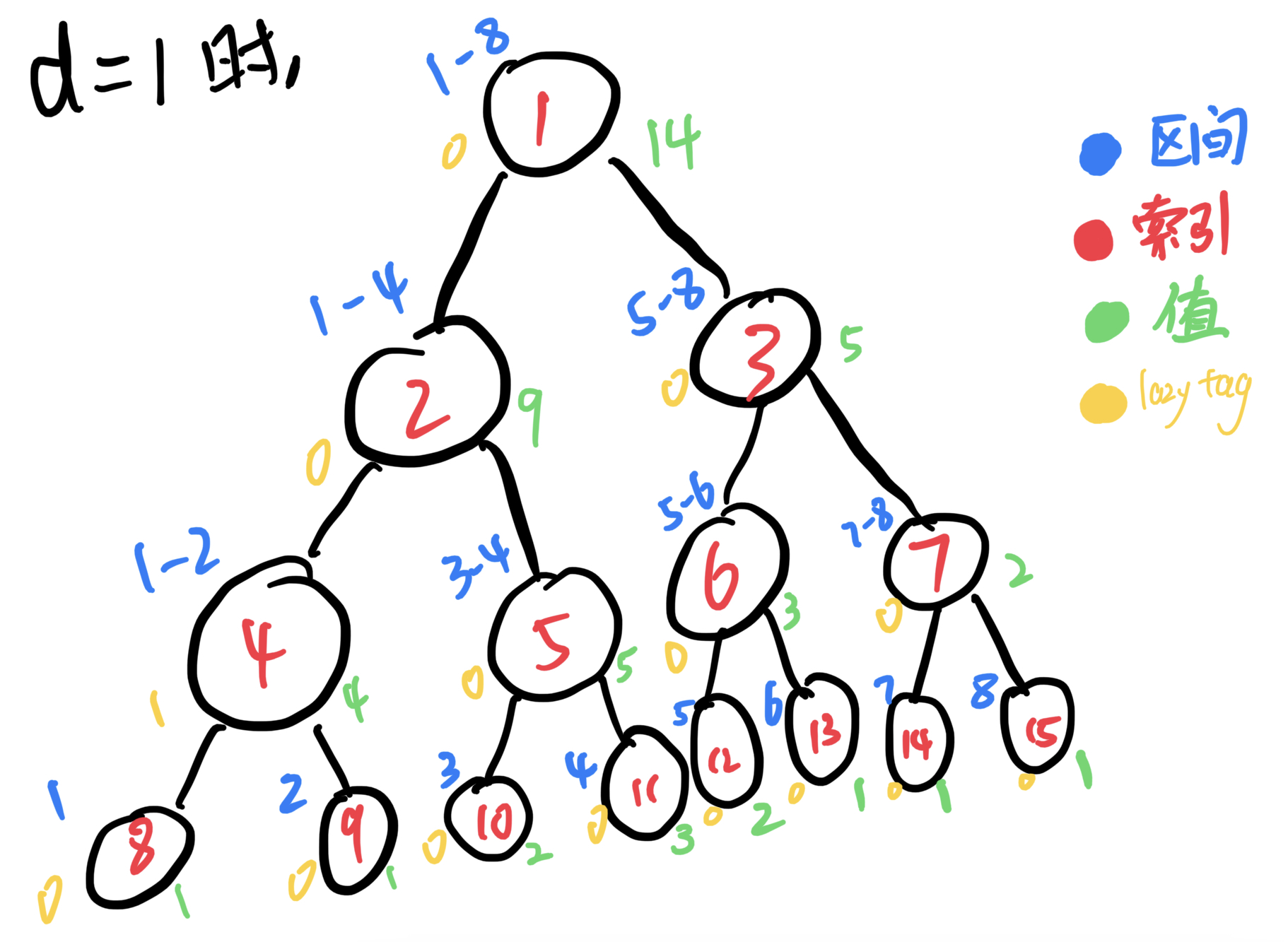
接下来就是看代码

void addtag(long long p,long long pl,long long pr,long long d)
{
    tag[p] += d;
    tree[p] += d*(pr-pl+1);
}
 
void push_dowm(long long p,long long pl,long long pr)
{
    if(tag[p])
    {
        long long mid = pl + pr >> 1;
        addtag(ls(p),pl,mid,tag[p]);
        addtag(rs(p),mid+1,pr,tag[p]);
        tag[p] = 0;
    }
}
 
// 区间修改 
void update(long long L,long long R,long long p,long long pl,long long pr,long long d)
{
    if(L<=pl && pr<=R)
    {
        addtag(p,pl,pr,d);
        return ;
    }
    // 向下传递
    push_dowm(p,pl,pr);
    long long mid = pl + pr >> 1;
    if(L<=mid) update(L,R,ls(p),pl,mid,d);
    if(R>mid) update(L,R,rs(p),mid+1,pr,d);
    tree[p] = tree[ls(p)] + tree[rs(p)];
}

查询

如果我要查询区间2~6 的和，我只需要查询节点9、5和3的值，将这些值加起来就是区间2~6 的和了。那么问题来了，我们怎么知道要查询节点9、5和3呢？不难看出，自上而下来查询，如果当前节点的区间被要查询的区间完全覆盖了，那么当前节点就是我们要找的结点，反之则需要继续往下查询。大家可以根据下面的图来模拟一下。

/**
 * L: 要查询区间的左端
 * R: 要查询区间的右端
 * p: 当前的结点索引
 * pl: 当前节点区间左端
 * pr: 当前节点区间右端
 */
long long query(long long L,long long R, long long p,long long pl,long long pr)
{
    // 如果要查询的区间能覆盖当前节点的区间，返回当前节点的值
    if(L<=pl && pr<=R) return tree[p];
    // 如果不能覆盖，则继续往下查询
    long long res=0;
    long long mid = pl + pr >> 1;
    if(L<=mid) res += query(L,R,ls(p),pl,mid);
    if(mid<R) res += query(L,R,rs(p),mid+1,pr);
    // 返回查询结果
    return res;
}

总结

​ 恭喜你看完了，你对线段树这个数据结构有了初步的了解，知道了他的建树和查询的过程。然而这些只是线段树的冰山一角，后面还有线段树的离散化、空间优化、多维推广、可持久化、非递归形式、子树收缩……蓝某杯不会考太难的线段树，但是肯定也不会简单，不然也不会有开篇的那位算法大佬的哀嚎了。（我是蒟蒻，我连蓝某杯有线段树的题目都不知道......）

练练手

https://www.luogu.com.cn/problem/P3372

https://www.luogu.com.cn/problem/P3373

https://www.luogu.com.cn/problem/P6242

https://blog.csdn.net/m0_49924838/article/details/122840892