红黑树总结
红黑树总结
红黑树用来解决什么问题?
在树型的查找中,我们知道二叉查找树的查找效率很不错,但是此树右个缺陷,就是对基本有序的树查找起来变成了二分查找法.效率低下.后来出现了平衡二叉树,解决了这个问题,但平衡二叉树无论是实现,还是其为了维护左右子树高度差问题的维护实现进而导致效率低下,进而产生了红黑树.
那些红黑树是不可能的?
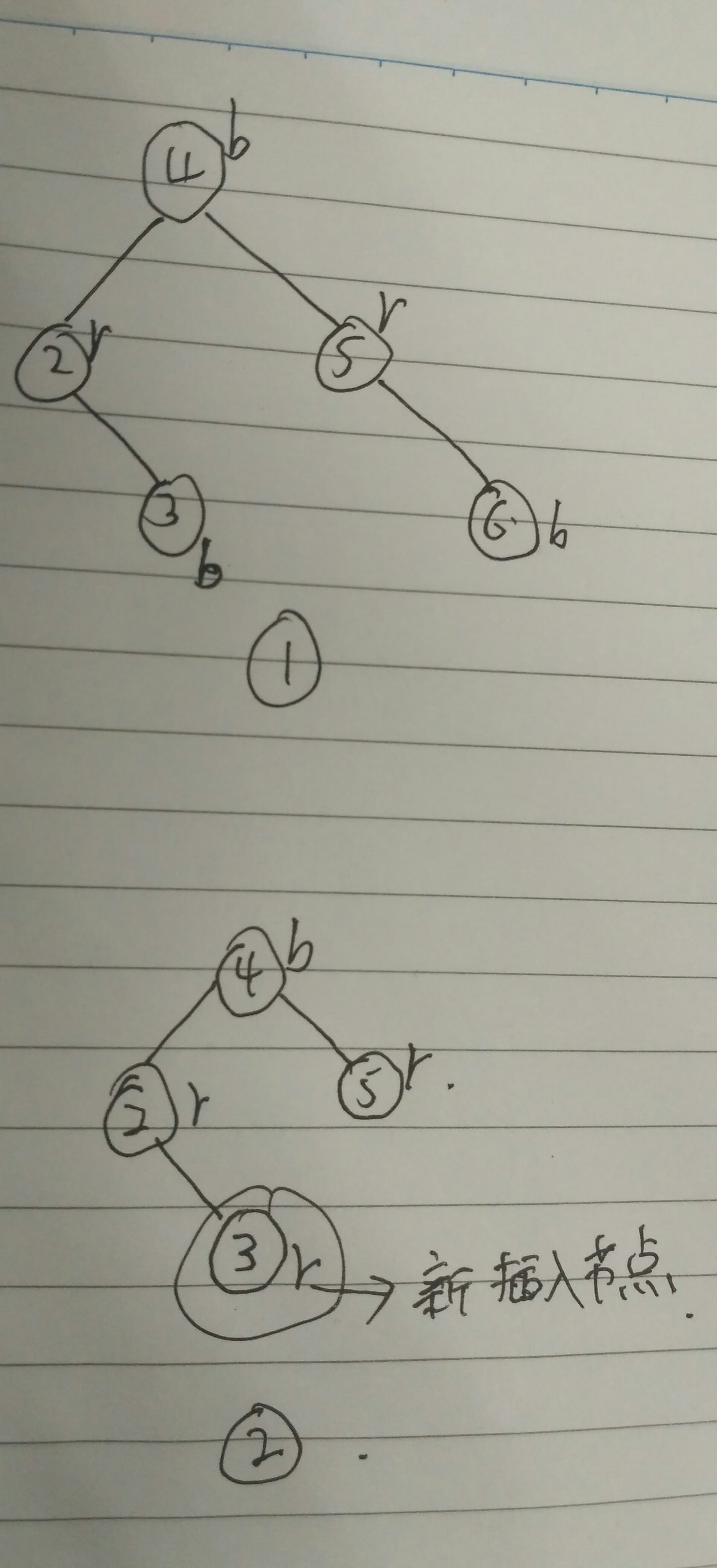
如上图,我们分析下这两个图:
-
图1是一个不可能的红黑树,因为最低下的节点3和6的颜色是黑色,这种节点是不可能这样添加上去的,还有每条路径不平衡,2的左子树虽然是个空节点,但是红黑树的叶子节点,因此其黑色高度为1,但是右边的红黑树高度明显大于1,因此我们有这样的结论:
- 当该节点没有孩子节点
- 该节点为红色,其父节点为黑色,兄弟节点为红色
- 该节点为黑色,此种节点一般是经过变换得来的,新插入的节点不可能是红色的.
- 当该节点只有左孩子或者右孩子之一,若该节点是黑色,其唯一孩子必然为红色,且孩子节点的左右子树必然为空节点.(这是由性质5决定的,为了左右子树的平衡,必须这样)
- 当该节点没有孩子节点
2. 图2是一个新插入节点3的典型的代表图,插入节点三以后,违反了性质4,则将节点2,5变为黑色,将4变为红色,然后再将4变为黑色即可.借此,我们分析一下插入节点的修复情况:(p:parent,g:grandfather,u:uncle)
1. 当插入节点是根节点时,直接将颜色变为黑色即可.
2. 当`p.color==BLACK`,而插入的节点为红色,对整个树不影响,不做调整.
3. 当`p.color==RED`,则p原来必然没有孩子,因此新插入的节点node是唯一孩子.`p.color==RED`->`g.color==BLACK(性质4)`->`u.color==RED(性质5)`,则将p,u颜色设置为黑色,将g颜色设置为红色,此时,问题变为g对整个树的影响,不一样了,后面讨论g的变化分类.
4. g变为了红色对整个树的影响,测试将g设置为新的节点node,注意这和插入不一样,这个节点是原本就有的.(此时对应插入节点的情况1,2一样不讨论,我们讨论此时node节点的父亲p的颜色是红色的情况,`p.color==RED`->`bro.color==BLACK`->`g.color==BLACK`->u可能为红色也可能为黑色,注意,此时并没有违反性质5,影响的只是性质4,两个连续的红色节点.此时处理的关键我们发现是u节点,因此对u分情况讨论)
1. 当`u.color==RED`,继续循环调用.
2. 当`u.color==BLACK`,见我前面的红黑树一节的说明,我们此时需要对节点g进行左旋(`p==g.right`)或右旋(`p==g.left`),但是此时由个问题,我们旋转后不希望继续出现继续违反性质4(两个节点为红色),因此需要对节点node是左子树还是右子树分情况讨论.
- 当`p==g.left`
- 当`node==g.left`,我们直接右旋,发现问题解决,OK!
- 当`node==g.right`,我们直接右旋,发现出现了节点g和bro同时为红色,且bro为g的左子树,违反性质4,这样的左旋肯定是有问题的.具体往下再不讨论,读者可以自己去想,我们得出的结论就是先将p节点左旋,然后再g节点右旋.然后我们会得到一个结论,此时的节点node变成了原来g节点的位置.为此,我们构造一颗树验证一下.
```java
@Test
public void testRBT() {
TreeMap<Integer, String> map = new TreeMap<>();
map.put(9, 9 + "");
map.put(3, 3 + "");
map.put(10, 10 + "");
map.put(1, 1 + "");
map.put(6, 6 + "");
map.put(4, 4 + "");
map.put(8, 8 + "");
assertThat(map.getFirstEntry().getKey(), is(9));
map.put(5, 5 + "");
assertThat(map.getFirstEntry().getKey(), is(6));
}
```
我们的结论被验证.
- 当`p==g.right`镜像问题,不再做讨论.
3. 综上: 我们分析一下整个插入过程,把能合并的合并.合并完之后就是我前一节红黑树所讨论的情况.在此,我们再综合一下.
- 当插入节点是根节点,变为黑色(case 1)
- 当`p.color==BLACK`,无需操作
- 当`p.color==RED`时:
- 当`u.color==RED`,递归解决(case 2)
- 当`u.color==BLACK`,若node节点和其父节点都是左子树或者都是右子树,直接旋转,否则需要先行处理,再旋转.(case 3)
我们给出这样的框架代码:
void fixInsertiong(Node node){
Node p,u,g;
while(node!=root&&node.parent.color==RED){
p=node.parent;
g==node.parent;
if(p==g.left){
u=g.right;
//case 2
if(u.color==RED){
u.color=BLACK;
p.color=BLACK;
g.color=RED;
node =g;
}
//case 3
else{
if(node==p.right){
rotateLeft(p);
Node tmp=p;
p=node;
node=tmp;
}
p.color=BLACK;
g.color=RED;
rotateRight(g);
}
}else{
u=g.left;
//case 2
if(u.color==RED){
u.color=BLACK;
p.color=BLACK;
g.color=RED;
node =g;
}
//case 3
else{
if(node==p.left){
rotateRight(p);
Node tmp=p;
p=node;
node=tmp;
}
p.color=BLACK;
g.color=RED;
rotateLeft(g);
}
}
}
}
//case 1
root.color==BLACK;
}
思路,由于新插入节点和及祖父节点变为红色时都需要调整,我们合并为一种情况,只考虑祖父节点变为红色,对整个树的影响,此时node.color==p.color==RED,bro.color==g.color==BLACK,故需要对u分颜色讨论,但是u的获取和p是左子树还是右子树有关,故先对p是左子树还是右子树分类,再对u.color分类,然后旋转,为了保证旋转后不会出现两个连续的红色,需要检查node节点和p是否都为左子树或者同为右子树.如果是直接旋转,如果不是,先逆向旋转,再旋转,这种情况得到的node一般变成了g的位置.






