BZOJ3624: [Apio2008]免费道路

考虑到这 k 条0边中肯定是有一些边是必须要加的
而其他的0边是可以被其他边替代的，并不影响连通性

那首先要确定哪些0边是必要的0边

先拿所有1边做生成树，然后考虑加入0边
加入后会使联通块个数减少的0边就是必须要加的
不过还有以下特殊情况：

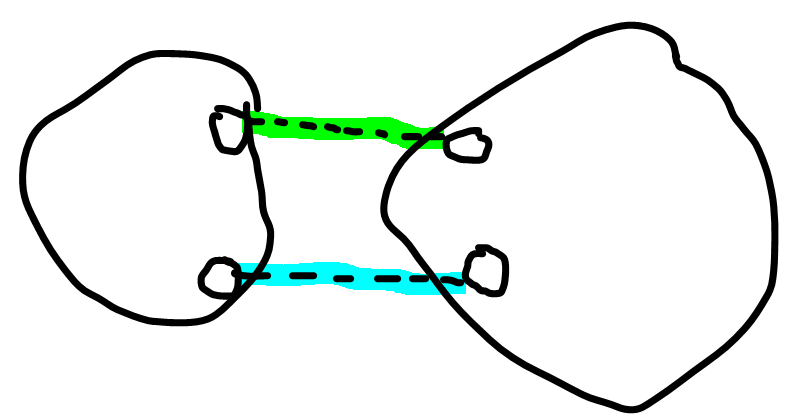
显然这两条边中只能找一条做为必要的边
那就找到了之后把它加进选入边集中就行

这时就会有一种不合法的情况，就是必需的边数 > k

之后把必需边加入的边先加进去
之后不断加入0边直到总共加入 k 条

这里又会出现不合法的情况，就是加不够 k 条

之后把所有1边加入就可以了

这里还会有一种不合法的情况，就是你建不出来一棵生成树

这样就可以过了

这题其实思路挺自然的，静下心来想肯定是会的

---

 代码：

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cctype>
#include <cstdio>
#include <locale>
using namespace std;
 
const int MAXN = 20005, MAXM = 100005;
 
struct EDGE {
    int x, y, typ;
    bool imp, intree;
}edge[MAXM];
int n, m, k, tot, blk;
int fa[MAXN];
 
inline int rd() {
    register int x = 0, c = getchar();
    while (!isdigit(c)) c = getchar();
    while (isdigit(c)) {
        x = x * 10 + (c ^ 48);
        c = getchar();
    }
    return x;
}
inline void resetfa() {
    for (int i = 1; i <= n; ++i) fa[i] = i;
}
int findfa(int x) {
    return ((fa[x] == x) ? (x) : (fa[x] = findfa(fa[x])));
}
inline bool link(int x, int y) {
    int fx = findfa(x), fy = findfa(y);
    if (fx == fy) return false;
    fa[fx] = fy;
    return true;
}
inline bool stick(int x, int y) {
    return (findfa(x) == findfa(y));
}
 
int main() {
    n = rd(); m = rd(); k = rd();
    resetfa();
    for (int i = 1; i <= m; ++i) {
        edge[i].x = rd(); edge[i].y = rd();
        edge[i].typ = rd();
    }
    for (int i = 1; i <= m; ++i) if (edge[i].typ) {
        link(edge[i].x, edge[i].y);
    }
    for (int i = 1; i <= m; ++i) if (!edge[i].typ && !stick(edge[i].x, edge[i].y)) {
        link(edge[i].x, edge[i].y);
        edge[i].imp = true;
        ++tot;
    }
    if (tot > k) {
        puts("no solution");
        return 0;
    }
    resetfa();
    blk = n;
    tot = 0;
    for (int i = 1; i <= m; ++i) if (edge[i].imp) {
        link(edge[i].x, edge[i].y);
        ++tot;
        --blk;
        edge[i].intree = true;
    }
    for (int i = 1; i <= m && tot < k; ++i) if (!edge[i].typ && !edge[i].imp) {
        if (link(edge[i].x, edge[i].y)) {
            ++tot;
            --blk;
            edge[i].intree = true;
        }
    }
    if (tot < k) {
        puts("no solution");
        return 0;
    }
    for (int i = 1; i <= m && blk != 1; ++i) if (edge[i].typ) {
        if (link(edge[i]. x, edge[i].y)) {
            --blk;
            edge[i].intree = true;
        }
    }
    if (blk != 1) {
        puts("no solution");
        return 0;
    }
    for (int i = 1; i <= m; ++i) if (edge[i].intree) {
        printf("%d %d %d\n", edge[i].x, edge[i].y, edge[i].typ);
    }
    return 0;
}