Theory of Computation

Model of Computation

Mathematical Logic

Def. Formal logical system consist of

An alphabet of symbols
A set of finite strings of these symbols, called well-formed formula (wf.)
A set of well-formed formulas, called axioms
A finite set of "rules of deduction"

Def. Perfect Logical System:

Soundness
Consistency
Completeness

Thm.[Gödel's completeness theorem] We have a complete first-order logic system.
Thm.[Gödel's incompleteness theorem] We cannot have a complete first-order arithmetic system.

Def. tautology/contradiction: a statement form that is always true/false.

Def. $A$ logically implies $B$ iff $A\rightarrow B$ is tautology. $A$ is logically equivalent to $B$ iff $A\leftrightarrow B$ is tautology.

Def. Rules for substitution：Replace the statement variables of a tautology with any statement form, the result will still be a tautology.

Thm. Every statement form is logically equivalent to a disjunctive/conjunctive normal form: $$(\vee_i(\wedge_j Q_{ij})),(\wedge_i(\vee_j Q_{ij})).$$

Thm. Adequate sets of connective: $\{\neg, \wedge\}, \{\neg, \vee\}, \{\neg, \rightarrow\},\{\text{NOR}\}, \{\text{NAND}\}.$

Statement logic

Formal Statement Calculus - L

Components:

Alphabet of symbols
Finite strings of these symbols, called well-formed formula (wf.)

Axioms:

(L1) $A \rightarrow (B \rightarrow A)$
(L2) $(A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C))$
(L3) $((\neg A) \rightarrow (\neg B)) \rightarrow (B \rightarrow A)$

Rules of Deduction:

Modus ponens (MP) From $A$ and $A \rightarrow B$, $B$ is a direct consequence

\[\vdash_L(A\to A) \]

\[\begin{aligned} (1)\ & (A\to ((B\to A)\to A)) & (L1) \\ (2)\ & ((A\to ((B\to A)\to A)) \to ((A\to (B\to A))\to (A\to A))) & (L2) \\ (3)\ & ((A\to (B\to A))\to (A\to A)) & (MP\ (1) (2)) \\ (4)\ & (A\to (B\to A)) & (L1) \\ (5)\ & (A\to A) & (MP\ (3) (4)) \end{aligned} \]

\[\{A, (B\to (A\to C))\} \vdash_L (B\to C) \]

\[\begin{aligned} (1)\ & A & (\Gamma) \\ (2)\ & (A\to (B\to A)) & (L1) \\ (3)\ & (B\to A) & (MP\ (1) (2)) \\ (4)\ & (B\to (A\to C)) & (\Gamma) \\ (5)\ & ((B\to (A\to C))\to ((B\to A)\to (B\to C))) & (L2) \\ (6)\ & ((B\to A)\to (B\to C)) & (MP\ (4) (5)) \\ (7)\ & (B\to C) & (MP\ (3) (6)) \end{aligned}\]

The deduction theorem: $\Gamma\cup \{A\} \vdash_L B$ iff $\Gamma \vdash_L (A\to B)$.

“Hypothetical Syllogism” (HS) $${(A\to B), (B\to C)} \vdash_L (A\to C).$$ Proof by the deduction theorem.

\[\vdash_L(\neg B\to(B\to A)) \]

\[\begin{aligned} (1)\ & (\neg B\to(\neg A\to \neg B)) & (L1) \\ (2)\ & ((\neg A\to \neg B)\to (B\to A)) & (L3) \\ (3)\ & (\neg B\to(B\to A)) & (HS(1)(2)) \\ \end{aligned}\]

\[\vdash_L \Bigl( (\neg A \to A) \to A \Bigr) \text{ by } \Bigl( (\neg A \to A) \Bigr) \vdash_L A \]

\[\begin{aligned} (1)\ & (\neg A \to A) & (\text{LI}) \\ (2)\ & (\neg A \to (\neg (\neg A \to A) \to \neg A)) & (\text{L3}) \\ (3)\ & \neg (\neg A \to A) \to \neg A & (\text{from (2), (3) HS}) \\ (4)\ & (\neg A \to (A \to \neg (\neg A \to A))) & (\text{L2}) \\ (5)\ & (\neg A \to (A \to \neg (\neg A \to A))) \to ((\neg A \to A) \to (\neg A \to \neg (\neg A \to A))) & (\text{L2}) \\ (6)\ & (\neg A \to A) \to (\neg A \to \neg (\neg A \to A)) & (\text{from (4), (5) MP}) \\ (7)\ & (\neg A \to \neg (\neg A \to A)) & (\text{from (1), (6) MP}) \\ (8)\ & (\neg A \to \neg (\neg A \to A)) \to ((\neg A \to A) \to A) & (\text{L3}) \\ (9)\ & ((\neg A \to A) \to A) & (\text{from (7), (8) MP}) \\ (10)\ & A & (\text{from (1), (9) MP}) \end{aligned} \]

Def. A valuation of $L$ is just an assignment of truth values to the variables of wfs.

Def. An extension of $L$ is a formal system obtained by enlarging the set of axioms so that all theorems of $L$ remain theorems.

Thm. Let $L^{*}$ be a consistent extension of $L$ and let $A$ be a wf. which is not a theorem of $L^*$. Then $L^{**}$, obtained from $L^*$ by including $(\neg A)$ as an additional axiom, is also consistent.

If $L^{**}= L^{*}\cup\{\neg A\}$ is not consistent, then $\vdash_{L^{**}} A$ , so $\{\neg A\}\vdash_{L^*}A$. Thus $\vdash_{L^*}(\neg A\to A)$ by the deduction theorem. Since $\vdash_{L^*}((\neg A\to A)\to A)$, we have $\vdash_{L^*} A$ , comes to a contradiction.

For all wfs. $A_0,A_1,...$, we add to $L_0=L$ one by one:

If $\vdash_{L_i}A_i$, then $L_{i+1}=L_i$,
Else $L_{i+1}=L_i\cup\{\neg A_i\}$.

Finally let $L^*=\bigcup_i L_i$. We can see $L^*$ is a consistent complete extension of $L$.

Let $L^*$ be a complete consistent extension of $L$, then there is a valuation in which each theorem of $L^*$ takes value T. Proof: we check the two operations $\neg$ and $\to$.

First-order logic

Term:
- variables and constants are terms
- if $t_1,t_2, ..., t_n$ are terms, then $f_i^n(t_1,t_2,..., t_n)$ is a term
Atomic formula:
- if $t_1,t_2, ..., t_n$ are terms, then $A_i^n(t_1,t_2, ..., t_n)$ is an atomic formula
Well-formed formula:
- every atomic formula
- if $A$ and $B$ are wfs., so are $(\neg A)$, $(A\to B)$ and $(\forall x_i)A$, where $x_i$ is any variable

Def. In $(\forall x_i)A$, we say that $A$ is the scope of the quantifier.

Def. An occurrence of $x_i$ in a wf. is said to be bound if it occurs within the scope of a $(\forall x_i)$ in the wf. or if it is the $x_i$ in a $(\forall x_i)$. Otherwise it is free.

Def(!!!). A term $t$ is free for $x_i$ in $a$ if $x_i$ doesn't occur free in $A$ within the scope of a $(\forall x_j)$, where $x_j$ is any variable occurring in $t$. Then $((\forall x_i) A(x_i)\to A(t))$ is true. i.e., $t$ can be substituted for free occurrence of $x_i$ in $A$ without interactions with quantifiers in $A$.

Def. An interpretation $I$ of $\mathcal{L}$ is a non-empty set $D_I$ (the domain of $I$) together with a collection of distinguished elements, a collection of functions on $D_I$, and a collection of relations on $D_I$.

Def. A valuation in $I$ is a function $v$ from the set of variables of $\mathcal{L}$ to the set $D_I$.

Def. A wf. $A$ is true in an interpretation in $I$ if every valuation in $I$ satisfies $A$.

Def. A wf. $A$ is logically valid / contradictory if $A$ is true/false in every interpretation of $\mathcal{L}$.

Def. A wf. $A$ of $\mathcal{L}$ is closed if no variable occurs free in $A$.

Formal system $K_{\mathcal{L}}$

Axioms

(K1) $A \rightarrow (B \rightarrow A)$.
(K2) $((A \rightarrow (B \rightarrow C)) \rightarrow ((A \rightarrow B) \rightarrow (A \rightarrow C)))$.
(K3) $((\neg A \rightarrow (B \rightarrow \neg B)) \rightarrow (B \rightarrow A))$.
(K4) $((\forall x) A \rightarrow A)$, if $x$ does not occur free in $A$.
(K5) $((\forall x) A(x) \rightarrow A(t))$, if $t$ is a term in $\mathcal{L}$ which is free for $x$ in $A(x)$.
(K6) $((\forall x)(A \rightarrow B) \rightarrow (A \rightarrow (\forall x) B))$, if $A$ contains no free occurrence of $x$.

Rules

Modus ponens: from $A$ and $A \rightarrow B$, deduce $B$.
Generalisation: from $A$, deduce $(\forall x)A$, where $x$ is any variable.

Thm. If $\Gamma\cup\{A\}\vdash_K B$, and $A$ is a closed wf., then $\Gamma\vdash_K(A\to B)$.

\[\vdash_{K}\Bigl((\forall x_i)\,A(x_i)\;\to\;(\forall x_j)\,A(x_j)\Bigr) \]

\[\begin{aligned} (1)\ & (\forall x_i)\,A(x_i)\to A(x_j) & (\text{K5})\\ (2)\ & (\forall x_j)\Bigl((\forall x_i)A(x_i)\to A(x_j)\Bigr) & (\text{Generalisation rule})\\ (3)\ & (\forall x_j)\Bigl((\forall x_i)A(x_i)\to A(x_j)\Bigr)\to\Bigl((\forall x_i)A(x_i)\to(\forall x_j)A(x_j)\Bigr) & (\text{K6})\\ (4)\ & (\forall x_i)A(x_i)\to(\forall x_j)A(x_j) & (\text{MP}(2),(3)) \end{aligned} \]

\[\vdash_K \Bigl( (\forall x_i)(A \to B) \Bigr) \to \Bigl( (\exists x_i) A \to B \Bigr) \]

\[\begin{aligned} (1)\ & (\forall x_i)(A \to B) \to (A \to B) & (\text{K4 or K5})\\ (2)\ & (A \to B) \to (\neg B \to \neg A) & (\text{K3})\\ (3)\ & (\forall x_i)(A \to B) \to (\neg B \to \neg A) & (\text{HS})\\ (4)\ & (\forall x_i)( (\forall x_i)(A \to B) ) \to (\neg B \to \neg A) & (\text{Generalisation})\\ (5)\ & (\forall x_i)( (\forall x_i)(A \to B) ) \to (\neg B \to \neg A) \to ((\forall x_i)(A \to B) \to (\forall x_i)(\neg B \to \neg A)) & (\text{K6})\\ (6)\ & (\forall x_i)(A \to B) \to (\forall x_i)(\neg B \to \neg A) & (\text{MP})\\ (7)\ & (\forall x_i)(\neg B \to \neg A) \to (\neg B \to (\forall x_i) \neg A) & (\text{K6})\\ (8)\ & \neg B \to (\forall x_i) \neg A & (\text{K3})\\ (9)\ & (\forall x_i)(A \to B) \to (\neg (\forall x_i) \neg A \to B) & (\text{2 HS steps}) \end{aligned} \]

Def.$(Q_1x_{i1})(Q_2x_{i2})...(Q_kx_{ik})D$ is a prenex form, where $D$ is a wf. of $\mathcal{L}$ with no quantifiers, and each $Q_j$ is either $\forall$ or $\exists$.

If $x_i$ does not occur free in $A$, then
- $\vdash_K (\forall x_i)(A \to B) \leftrightarrow (A \to (\forall x_i)B)$
- $\vdash_K (\exists x_i)(A \to B) \leftrightarrow (A \to (\exists x_i)B)$
If $x_i$ does not occur free in $B$, then
- $\vdash_K (\forall x_i)(A \to B) \leftrightarrow ((\exists x_i)A \to B)$
- $\vdash_K (\exists x_i)(A \to B) \leftrightarrow ((\forall x_i)A \to B)$

Thm. Any wf. 𝓐 is equivalent to a wf. 𝓑 in prenex form.

Def. A wf. in prenex form is a $\Pi_n$- form if it starts with a universal quantifier and has $n-1$ alternations of quantifiers.
A wf. in prenex form is a $\Sigma_n$- form if it starts with an existential quantifier and has $n-1$ alternations of quantifiers.

Thm. Substitution: let $A$ and $B$ are closed wfs. of $L$, and suppose that $B_0$ arises from the wf. $A_0$ by substituting $B$ for one or more occurrences of $A$ in $A_0$. Then

\[\vdash_K (A \leftrightarrow B) \to (A_0 \leftrightarrow B_0). \]

Finite Automata & Context Free Grammar

DFA, NFA and Regular language

Language, machine and DFA

Def. Formal Languages:

Alphabet $\Sigma$
String $\Sigma^*=\{\varepsilon\}\cup\Sigma\cup\Sigma^2\cup...$
Language $L\subseteq \Sigma^*$

Def. Machine is a function $M(x)=y$ where $x\in \Sigma,y\in \{\text{accept},\text{reject}\}$. $L(M)= \{ x|M \text{ accepts } w\} .$

Def. Deterministic Finite Automata is a $5$-tuple ($Q,\Sigma,\delta,q,F$):

$Q$ is a finite set of states.
$\Sigma$ is a finite set of symbols.
$\delta:Q\times \Sigma\to Q$ is the transition function
$q\in Q$ is the start state
$F\subseteq Q$ is the set of accepting states

This is the syntax definition. Or you can directly define as "the machine accepts string $w$" (semantics).

Def. DFA $M$ accepts $w=w_1w_2...w_n$ iff $\exists (r_0,r_1,...,r_n)$ where $r_0=q,r_i=\delta(r_{i-1},w_i),r_n\in F$.

Def. Regular Languages: The set of all languages recognized by some DFA.

Closure properties

Thm. The class of regular languages is closed under complementation.

Pf. $M'$ identical to $M$, except with final states $Q-F$.

Thm. The class of regular languages is closed under intersection.

Pf. $M_3=(Q_1\times Q_2,\Sigma,\delta_3,(q_1,q_2),F_1\times F_2)$ where $\delta_3((r_1,r_2),a)=(\delta_1(r_1,a),\delta_2(r_2,a))$.

Concatenation is hard.

Nondeterministic Finite Automata

Def. Nondeterministic Finite Automata is a $5$-tuple ($Q,\Sigma,\delta,q,F$):

$Q$ is a finite set of states.
$\Sigma$ is a finite set of symbols.
$\delta:Q\times \Sigma_{\varepsilon}\to 2^Q$ is the transition function
$q\in Q$ is the start state
$F\subseteq Q$ is the set of accepting states

Def. NFA $M$ accepts $w$ iff $w$ can be written as $x_1x_2...,x_m$ by adding any number of $\varepsilon$ ($w$ is a subsequence of $x$) s.t. $\exists (r_0,r_1,...,r_m)$ where $r_0=q,r_i\in\delta(r_{i-1},x_i),r_m\in F$.

Equivalence of NFA and DFA

Thm. For any DFA $M$, there is a NFA $N$ such that $L(M) = L(N)$.

Trivial.

Thm. For any NFA $N$, there is a DFA $M$ such that $L(N) = L(M)$.

Pf. For any NFA $N = (Q,\Sigma,\delta,q,F)$, define a DFA $M=(Q',\Sigma,\delta',q',F')$:

$Q'=2^Q$
$\delta'(R, a)=E(\bigcup\limits_{r\in R}\delta(r,a))$
$q'=E(q)$
$F'=\{R|R\cap F\neq\emptyset\}$

here $E(R)=\{r\in Q| r \text{ is reachable from }R\text{ using zero or more }\varepsilon-\text{transitions}\}$.

Closure properties

NFA is closed under union, concatenation and star.

Regular Expressions

Def. A Regular expression is a string over $\Sigma, \emptyset, \varepsilon,\cup,\circ ,^*,(,)$

Def. Generalized NFAs: Transitions are REGEXPs, not just symbols from $\Sigma_\varepsilon$.

\[\delta:(Q-\{q_f\})\times(Q-\{q_s\})\rightarrow \text{REGEXP} \]

Rem. GNFA only has one accept state. The accept state can't transfer to other state and the start state can't be transfered from other state.

Thm. REGEXPs equivalent to NFAs.

Pf. Only need to prove that every language recognized by an NFA can be represented as a REGEXP. Converse is obvious. Showing GNFA $\subseteq$ REGEXP is sufficient, since NFA $\subseteq$ GNFA.

The high-level idea is to reduce the size of GNFAs. If we want to get rid of a state $q_{rip}\in Q$, for any $q_i,q_j\in Q$, replace $\delta(q_i,q_j)$ by

\[\delta(q_i,q_j)\cup \delta(q_i,q_{rip})\delta(q_i,q_{rip})^* \delta(q_{rip},q_j). \]

We can delete all non-start/accept states one by one. Until it only have with 2 states, obviously it's equivalent to a REGEXP.

CFG and PDA

Context Free Grammar

Def. A Context-free grammar (CFG) is a 4-tuple $(V,\Sigma,R,S)$:

$V$ is a set of variables;
$\Sigma$ is a set of terminals;
$R$ is a set of rules (a variable and a string in $(V\cup \Sigma)^*$);
$S\in V$ is the start variable.

Semantics:

$uAv\Rightarrow uwv$ ($uAv$ yields $uwv$) if $A\rightarrow w$ is a rule $r\in R$;
$u\Rightarrow^*v$ ($u$ derives $v$) if $\exists u_1,u_2,...,u_k$ s.t.

\[u\Rightarrow u_1\Rightarrow u_2\Rightarrow...\Rightarrow u_k\Rightarrow v. \]

**Def. ** The language of a CGF $G=(V,\Sigma,R,S)$ is defined as:

\[L(G)=\{w\in\Sigma^*|S\Rightarrow^*w\}. \]

Ex. $L=\{0^n1^n| n\ge 0\}$ is not regular, but is context-free ($S\rightarrow0S1\mid \varepsilon$).

Thm. Every regular language is context-free.

Pf. Given a DFA $A = (Q,\Sigma,\delta,q_0,F)$, we need to find an equivalent CFG $A’ = (V,\Sigma',R,S)$ s.t. $L(A)=L(A')$. Make a variable $R_i$ in $A'$ for every state $q_i$ in $A$. Add the rule $R_i\to aR_j$ to $A’$ if $\delta(q_i, a)=q_j$ in $A$. $R_0$ is the start variable if $q_0$ is the start state. Add the rule $R_i\to \varepsilon$ if $q_i$ is an accept state in $A$.

We can use Parse Tree to represents the rules used to generate a string.

Def. A grammar is called ambiguous if a string has two distinct parse trees.

Leftmost derivation: at every step the leftmost remaining variable is the one replaced. Ambiguous equivalent to having two different leftmost derivations.

Ex (Polish notation). $\text{EXPR} \rightarrow a\mid b\mid c;\text{EXPR}\rightarrow+\text{ EXPR }\text{EXPR}\mid -\text{ EXPR }\text{EXPR}\mid \times\text{ EXPR }\text{EXPR}\mid /\text{ EXPR }\text{EXPR}.$

Thm. Checking whether a CFG is ambiguous is undecidable.

Def. A CFL is called inherently ambiguous if every CFG for the language is ambiguous.

Ex. $L=\{w\mid w=a^ib^jc^k,i,j,k\ge 1\wedge (i=j\vee i=k)\}$ is inherently ambiguous.

Thm. CFLs are closed under union, concatenation and kleene star.

Rem. CFLs are NOT closed under intersection.

Pushdown Automaton

Def. A pushdown automaton is a 6-tuple $(Q, \Sigma, \Gamma, \delta, q_0, F)$:

$Q$ is a finite set of states;
$\Sigma$ is the input alphabet;
$\Gamma$ is the stack alphabet;
$q_0\in Q$ is the initial state;
$F\subseteq Q$ is a set of final states;
$\delta: Q\times \Sigma_{\varepsilon}\times\Gamma_\varepsilon\to 2^{Q\times \Gamma_\varepsilon}$ is the transition function.

where $\Sigma_{\varepsilon}=\Sigma \cup \{\varepsilon\},\Gamma_\varepsilon=\Gamma\cup\{\varepsilon\}$.

It accepts string $w\in\Sigma^*$ if

$w$ can be written as $x_1x_2...x_m$ where $x_i\in\Sigma_\varepsilon$;
$\exists r_0,r_1,...,r_m\in Q$;
$\exists s_0,s_1,...,s_m\in\Gamma^*$

such that

$r_0=q_0,s_0=\varepsilon$;
$(r_i,b)\in\delta(r_{i-1},x_i,a)$, where $s_{i-1}=at$ and $s_i=bt$ for $1\le i\le m$;
$r_m\in F$.

Thm. A language $L$ is context-free if and only if it is accepted by some pushdown automaton.

Pf. CFGs $\to$ PDAs: Push $\$$ and $S$ onto stack, then repeat the following steps:

If the top of the stack is a variable $A$: Choose a rule $A\to \alpha$ and substitute $A$ with $\alpha$;
If the top of the stack is a terminal $a$: Read next input symbol and compare to $a$.
- If they don’t match, reject;
- Otherwise, pop $a$;
If top of stack is $\$$, go to accept state.

PDAs $\to$ CFGs: First, we simplify the PDA s.t.

It has a single accept state $q_f$;
It empties its stack before accepting;
Each transition is either a push, or a pop.

For PDA $P=(Q, \Sigma, \Gamma, \delta, q_0, F)$ satisfying above conditions, construct the CFG $G=(V,\Sigma',R,S)$:

$V=\{A_{pq}|\forall p,q\in Q\}$ where $A_{pq}=\{x:x \text{ leads from state }p\text{ with an empty stack to state q with an empty stack}\}$.
$S=A_{0f}$.
$R=\{A_{pq}\to A_{pr}A_{rq}|\forall p,q,r\in Q\}\cup \{A_{pq}\to aA_{rs}b|\forall p,q,r,s\in Q,t\in\Gamma,(r,t)\in\delta(p,a,\varepsilon),(q,\varepsilon)\in\delta(s,b,t)\}\cup \{A_{pp}\to\varepsilon|\forall p\in Q\}.$

We can show that $L(P)=L(G)$.

Pumping Lemma

Nonregular Languages

Ex. $\{0^n1^n|n\ge 0\}$ is nonregular. For any $k$ states DFA $M$, by Pigeonhole principle, there exists $0\le i\neq j\le k$ s.t. $M$ is on the same state after reading $0^i$ or $0^j$. Thus if $M$ accepts $0^i1^i$, it must accepts $0^j1^i$.

Thm (Pumping Lemma). If $A$ is a regular language, then there is a number $p$ (the pumping length) where, if $s$ is any string in $A$ of length at least $p$, then $s$ can be divided into $s=xyz$, satisfying

For each $i\ge 0$, $xy^iz\in A$
$|y|>0$
$|xy|\le p$

Pf: Let $ M = (Q, \Sigma, \delta, q_{\text{start}}, F) $ be a DFA recognizing $ A $ and $ p $ be the number of states of $ M $. For any string $s$ s.t. $ |s| \geq p $, let $ q_0 = q_{\text{start}}, q_i = \delta(q_{i-1}, s[i])$. By pigeonhole principle, there exist $ q_i = q_j $ ($i \neq j$). So let $$ x = s[1, \ldots, i], y = s[i+1, \ldots, j], z = s[j+1, \ldots, p] $$ ($z$ can be empty). $ xy^i $ will also reach $ q_i $, so if $ xyz \in A $, then $ xy^i z \in A $.

Ex. $F=\{ww|w\in\{0,1\}^*\}$. $s=0^p10^p1\in F$ but $xy^2z=0^{p+i}10^p1\notin F$.

$D=\{1^{n^2}|n\ge 0\}$. $s=1^{p^2}\in D$ but $xy^2z=1^{\le p^2+p}\notin F$.

$\{0^i1^j|i>j\}$ is not regular.

Non context-free Languages

Thm. If $A$ is a context-free language, then there is a number $p$ (the pumping length) where, if $s$ is any string in $A$ of length at least $p$, then $s$ may be divided into $5$ pieces $s=uvxyz$, satisfying:

For each $i\ge 0$, $uv^ixy^iz\in A$;
$|vy|>0$;
$|vxy|\le p$.

Pf. Let $v$ be the number of variables, $b$ be the maximum number of symbols in the right-hand side of the rules. Let $p=b_{v+1}$. Assume $s$ is any string in $A$ of length at least $p$. Consider a parse tree of $s$, by pigeonhole principle, there exists a path of length at least $v+1$. Furthermore, we can find two nodes with the same label on this path. Denote them as $x$ and $y$, assume $x$ is an ancestor of $y$. Let $x$ be the subtree of $y$ and $vxy$ be the subtree of $x$.

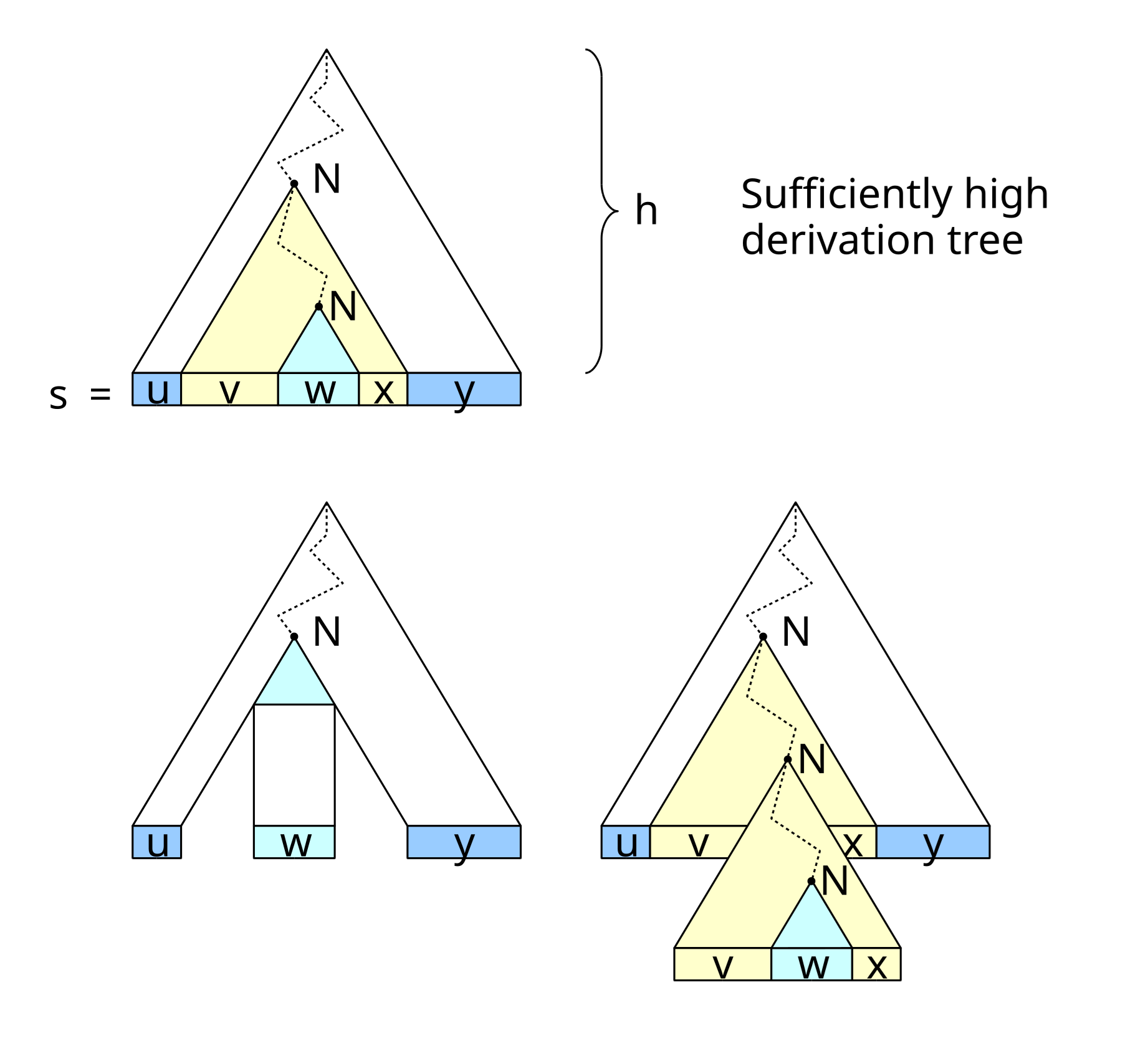
Ex. $\{a^nb^nc^n|n\ge 0\}$ and $\{ww|w\in\{0,1\}^*\}$ is not context-free.

For the former, consider $z=a^pb^pc^p$. Since $|vxy|\le p$, $vxy$ cannot contain all three of the symbols $a,b,c$, because there are $p$ $b$s. So $vxy$ either does not have any $a$s or does not have any $b$s or does not have any $c$s. Suppose, w.l.o.g., $vxy$ does have any $a$s. Then $uv^0 x y^0 z = uxz$ contains more $a$s than either $b$s or $c$s. Hence $uxz\notin L$.

For the latter, consider $s=0^p1^p0^p1^p$.

Turing Machine

DTM, NTM, and Variants

Standard Turing machine

Def. A Turing machine is a 7-tuple:

$Q$ is the set of states
$\Sigma$ is the input alphabet
$\Gamma$ is the tape alphabet
$\delta:Q\times\Gamma\to Q\times \Gamma\times\{L,R\}$ is the transition function
$q_{\text{start}}\in Q$
$q_{\text{accept}}\in Q$
$q_{\text{reject}}\in Q$

satisfying $\Sigma\cup\{\perp\}\subseteq\Gamma,q_{\text{accept}}\neq q_{\text{reject}}$.

Def. A configuration is a list of the tape contents, head position, and state.

Def. $L(M) = \{w\in\Sigma* \mid \text{starting with }w\text{ on the first }|w|\text{ cells of the tape, }M\text{ will eventually enter the accept state}\}.$

Def.

$M$ recognizes a language $A$ if $L(M)=A$. A language is recursively enumerable (or recognizable) if some Turing machine recognizes it.
$M$ decides $A$ if $L(M)=A$ and $M$ always halts. A language is recursive (or decidable) if some Turing machine decides it.
$L$ is co-recognizable if $L$ is recognizable.

Thm. A language is decidable iff it is recognizable and co-recognizable.

Ex. $L=\{0^{2^n}|n\ge 0\}$.

Thm. The set of Turing machines is countable.

Def. Universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input.

Thm. Universal Turing machine exists.

Pf. Can be implemented by a 3-tape TM:

The first one stores the description of the input machine.
The second one stores the tape content.
The third one stores the state.

Rem. There is a universal TM with 2 states and a 3-symbol alphabet. It's the smallest universal TM.

We will introduce several variants of TMs, and see that these variants are all equivalent to standard TM.

Multitape Turing Machines

Update the configuration on all the tapes simultaneously.

Thm. A language is Turing-recognizable if and only if some multitape Turing machine recognizes it.

Pf. The following simulation algorithm immediately prove the 2-tape case. (The head is at the first cell marked •)

Add a • to the first symbol 0/1
Write a '#' at the end of the input
Write a ⊥• after the #
Repeat:
- Note the symbol $x$• in the current cell.
- Move the head to the second • , note the symbol $y$• in that cell.
- If the left head tries to move to the #, shift # and all of tape 2 to the right.
- Apply the transition $\delta(q,x,y) = (q’,x’,y’,m,m’)$ to the second •.
- …then to the first.
- Stop if $q' = q_{\text{accept}}$ or $q_{\text{reject}}$.

Nondeterministic T.M.s

The NTM accepts a string if there is SOME sequence of guesses that yields an accepting configuration.

Thm. A language is Turing-recognizable if and only if some nondeterministic Turing machine recognizes it.

Pf. It will be shown that how to simulate an NTM with a 3-tape TM. The information on 3 tapes:

Tape 1 holds the input (don’t write anything else here)
Tape 2 is a simulation tape
Tape 3 holds the nondeterministic guesses

Do the breadth-first search:

Initially tape 1 contains the input, tapes 2 and 3 are empty
Copy tape 1 to tape 2
Use tape 2 to simulate the NTM with the input. Use tape 3 as choices for all branches. If no more symbols on tape 3, or if the nondeterministic choice is invalid, or the NTM reject, goes to step 4. If it accepts, accept the input.
Replace the string on tape 3 with the lexicographically next string. Go to step 2. (the string on tape 3 becomes longer and longer)

We call a nondeterministic Turing machine a decider if all branches halt on all inputs.

Thm. A language is decidable if and only if some nondeterministic Turing machine decides it.

TM with outputs

TM with an extra "write-only tape": whenever print, cannot erase

Def. Enumerator is a Turing machine with a printer.

Thm. A language is Turing-recognizable if and only if some enumerator generates it.

Pf. $\Rightarrow$ Enumerate the step number $i$ and a string $s_j$, run the first $i$ steps of $M(s_j)$.

$\Leftarrow$ Run the enumerator, every time that it outputs a string, compare it with the input string.

Reducibility

Gödel’s Entscheidungsproblem

Def. The Entscheidungsproblem asks for an algorithm that takes as input a statement of a first-order logic (possibly with a finite number of axioms beyond the usual axioms of first-order logic) and answers "Yes" or "No" according to whether the statement is universally valid, i.e., valid in every structure satisfying the axioms.

Thm. A general solution to the Entscheidungsproblem is impossible.

Def. Let $A_{\text{TM}}=\{\langle M,w\rangle\mid M \text{ is a TM and }M\text{ accepts }w\}.$

Thm. $A_{\text{TM}}$ is recognizable, but not decidable.

Pf. We prove the latter by contradiction.

Assume $A_{\text{TM}}$ is decidable, then there is a TM $H$ that decides $A_{\text{TM}}$. Construct a procedure $D$ with input <$M$> (<$M$> is the description of a TM) :

D(<M>): 
	if H(<M,<M>>) accepts
        return reject;
 	else
		return accept;

Note that $D$ always halts since $H$ always halts. We can see that $D(\text{<} D\text{>})$ always halts.

Prop. $A_{\text{TM}}$ is not co-recognizable.

Halting Problem

Def. $\text{HALT}_{\text{TM}} = \{\langle M,w\rangle | \text{TM } M \text{ halts on input }w\}.$

Thm. $\text{HALT}_{\text{TM}}$ is not decidable.

Pf. Reduction from $A_{\text{TM}}$.

Def. Oracle Turing Machine (OTM): a TM capable of querying an oracle

multitape TM $M$ with special “query” tape
and special states $q_{\text{query}}, q_{\text{yes}}, q_{\text{no} }$
on input $x$, with oracle language $A$
$M^A$ runs as usual, except…
when $M^A$ enters state $q_{\text{query}}$:
- $y = \text{contents of query tape}$
- $y \in A$ ⇒ transition to $q_{\text{yes}}$.
- $y \notin A$ ⇒ transition to $q_{\text{no}}$.

Def. Language $A$ is Turing reducible to $B$, if an oracle TM $M^B$ decides $A$, write $A\le_TB$.

Thm. If $A\le_T B$ and $B$ is decidable, then $A$ is decidable.

Ex. We have $A_{\text{TM}}\le_T\text{HALT}_{\text{TM}}$. From $A_{\text{TM}}$ is undecidable, $\text{HALT}_{\text{TM}}$ is also undecidable.

Thm [Kleene’s s-m-n Theorem]. Suppose we have a TM $M(x_1,…,x_m, y_1,…,y_n)$ whose input is composed of $m+n$ variables. There is a TM $T(\text{<}M\text{>}, x_1,…,x_m)$ when given $M, x_1,…,x_m$, outputs a TM $M’$ such that $M'(y_1,…,y_n)=M(x_1,…,x_m, y_1,…,y_n)$.

Ex. For a set of language $S$, if exists $L(M_0)\in S$ and $L(M_1)\notin S$, then $\mathcal{L}=\{M|L(M)\in S\}$ is undecidable. To prove $\text{HALT}_{\text{TM}}\le_T L$, consider construct a TM $T$ with input $z$:

Input 〈M, w〉, where M is a TM and w is a string
Simulate M on input w
if M halts on w
	return M0(z);
else
	return M1(z);

Clearly, $L(T)\in \mathcal{L}$ iff $\langle M,w\rangle\in\text{HALT}_{\text{TM}}$.

The Post Correspondence Problem

Def. The Post Correspondence Problem (PCP) : Given a set of dominos, find a sequence of these dominos so that the string we get by reading off the symbols on the top is the same as the string of symbols on the bottom. In other words,

\[PCP = \{D| D\text{ is a collection of tiles that contains a top-bottom match}\}. \]

Thm. $PCP$ is undecidable.

Pf. Consider reduction from $A_{\text{TM}}$. W.l.o.g., assuming TM $M$ erase its tape and one of the PCP dominos is marked as the starting domino.

Let $\left[\dfrac{\#}{\#q_0w\#}\right]$ be the starting domino. $\left[\dfrac{qa}{bq'}\right]$ for all $\delta(q,a)=(q',b,R)$ and $\left[\dfrac{cqa}{q'ba}\right]$ for all $\delta(q,a)=(q',b,L)$ and $c$. $\left[\dfrac{a}{a}\right]$ for all $a$. $\left[\dfrac{☐\#}{\#}\right],\left[\dfrac{\#q_a}{\varepsilon}\right],\left[\dfrac{☐}{\varepsilon}\right]$.

Reductions via computation histories

Ex. $ALL_{\text{CFG}}=\{\braket{G}:G\text{ is a CFG that generates all strings}\}$ is undecidable.

Consider the following reduction from $A_{\text{TM}}$ to $ALL_{\text{CFG}}$: For input $\braket{M},w$, construct a CFG G s.t. $M$ accepts $w$ iff $G$ does not generate its computation histories, and $G$ generates all strings otherwise.

How to achieve it? Construct a PDA $D$ that accepts strings of computation histories meeting one of the following conditions:

Do not start with an starting configuration;
Do not end with an accepting configuration;
Some $C_i$ does not yield $C_{i+1}$ legally.

In order to make the language to be context-free, the strings accepted is arranged as:

\[\#C_1\#C_2^R\#C_3\#C_4^R... \]

Thus $ALL_{\text{CFG}}$ is undecidable.

Thm. For context-free grammars:

Universality, equivalence and ambiguity is undecidable;
Emptiness, finiteness, membership is decidable.

Mapping reducibility

Def. A function is a recursive function if some Turing machine $M$, on every input $w$, halts with just $f(w)$ on its tape.

Def. Language $A$ is mapping reducible to language $B$, if there is a recursive function $f$, such that $w\in A \Leftrightarrow f(w)\in B$, denoted $A\le_m B$. The function $f$ is called the reduction of $A$ to $B$. (also called “many-one reduction”)

Thm. If $A\le_m B$ and $B$ is decidable, then $A$ is decidable.

Thm. If $A\le_m B$ and $B$ is Turing-recognizable, then $A$ is Turing-recognizable.

Ex. $EQ_{\text{TM}}=\{\braket{M_1,M_2}| M_1\text{ and }M_2\text{ are TMs and }L(M_1)=L(M_2)\}.$

By Turing reducibility, we show that $EQ_{\text{TM}}$ is undecidable.

By mapping reducibility, we show that $EQ_{\text{TM}}$ is neither recognizable nor co-recognizable, using the following reduction:

f(<M,w>):
	Define M1 which rejects all inputs
    Define M2 which simulates M on input w
    Output <M1,M2>

Def. $\text{TIME}(t(n))$: all languages that are decidable by an $O(t(n))$ time deterministic Turing machine.

$\text{NTIME}(t(n))$: all languages that are decidable by an $O(t(n))$ time nondeterministic Turing machine.

Def. $\text{P}=\bigcup_k\text{TIME}(n^k),\text{NP}=\bigcup_k\text{NTIME}(n^k)$.

For proving NP-completeness, we use polynomial-time many-one reductions.

Recursion Theorem

Thm [Recursion Theorem]. Let $t:\mathbb{N}\to\mathbb{N}$ be a recursive function. There is a TM $F$ for which $t(\braket{F})$ is the code of a Turing machine equivalent to $F$.

Pf. Consider let $\braket{F}=D(\braket{V})$, $D$ and $V$ is given as follows:

D(<M>) {
	output the code of the Turing machine G: 
	G(y) {
 		run the machine with code M(<M>) on y;
 	}
}
V(<M>) {
	output t(D(<M>));
}

We can see that $F$ is decribed as follows:

F(y) {
	run the machine with code V(<V>) on y;
}

Thus $$\braket{F}=V(\braket{V})=t(D(\braket{V}))=t(\braket{F}).$$

Thm [Kleene’s recursion theorem]. Let $t$ be a recursive function $t: \mathbb{N}\times\mathbb{N}\to\mathbb{N}$. There is a Turing machine $R: \mathbb{N}\to\mathbb{N}$, where $$R(x)=t(\braket{R},x).$$

Pf. Define the recursive function $s: \mathbb{N}\to\mathbb{N}$ as follows (by s-m-n theorem), and apply recursion theorem on $s$.

s(x) {
	output the code of the TM on input y computing t(x,y);
}

Thus $$R(x)= \text{``simulating the TM with code }s(\braket{R})\text{ on }y''=t(\braket{R},y).$$

Ex. Another proof of ATM is undecidable.

Pf. Suppose $H(\braket{M,w})$ decides $A_{\text{TM}}$:

B(w):
     Obtain, via the recursion theorem, own description <B>
     Run H(<B,w>)
     Accept if H rejects, reject if H accepts

Ex. $\text{MIN}_{\text{TM}} =\{\braket{M}| M\text{ is a “minimal” TM, that is, no TM with a shorter encoding recognizes the same language}\}$ is not recursively enumerable.

Pf. Assume $\text{MIN}_{\text{TM}}$ is r.e., then there is an enumerator $E$ which lists all strings in it.

R(w): 
	Obtain <R>;
	Run E, producing list <M1>, <M2>, ... of all minimal TMs
    until you find some <Mi> with |<Mi>| strictly greater than |<R>|;
    Return Mi(w);

Then $R$ is equivalent to $M_i$, but shorter than $M_i$, a contradiction.

Def. A quine is a non-empty computer program produces a copy of its own source code which takes no input and as its only output.

Thm. There is a quine. (By recursion theorem.)

*Kolmogorov complexity

Def. The minimum description $d(x)$ of $x$ is the shortest string $\braket{M,w}$ where TM $M$ on input $w$ halts with $x$ on its tape.

Def. The Kolmogorov complexity $K(x)=|d(x)|.$

Thm. For all $x$, $K(x^n)≤|x|+c·\log n$, for some constant $c$.

Def. A string $x$ is $c$-compressible if $K(x)≤|x|-c$. If $x$ is not $1$-compressible, we say that $x$ is incompressible.

Thm. Incompressible strings of every length exist.

Thm. $$\text{Pr}_{x\in{0,1}^n} [K(x)\ge |x|-c]\ge 1-2^{-c}.$$

Pf. $\#(\text{binary string of length }n)=2^n, \#(\text{description of length}<n-c)\le 2^{n-c}-1.$

Thus $$\text{Pr}_{x\in{0,1}^n } [K(x)< n-c]\le\frac{2^{n-c} -1}{2^n }<2^{-c}.$$

Def. $\text{COMPRESS}=\{(x,c)| K(x)≤c\}$.

Thm. COMPRESS is undecidable.

Pf. Suppose COMPRESS is decidable, construct a machine $M$:

M(n):
	For all y in lexicographical order:
		If (y,n) ∉ COMPRESS, print y and halt

We can see that the output $y$ is the first string of Kolmogorov complexity $>n$.

But $M(n)$ prints $y$, and $K(y)≤ |\braket{M,n}|=c+\log n$, a contradiction for large enough $n$.

Thm [Chaitin's incompleteness theorem]. Suppose in a formal system $F$:

Any mathematical statement describable in English can also be described within $F$.
Proofs are convincing: given $(S,P)$, it is decidable to check that $P$ is a proof of $S$ in $F$.

Then for large enough $L$, for all $x$, $K(x)>L$ is not provable.

Pf. Suppose we can prove $K(x)>L$ for some $x$. Pick the smallest such proof $P$ which proves $K(y)>L$. Consider the machine $R$:

R(L):
	For all list of w.f. Q in lexicographical order:
        Check whether Q is a valid argument
        Check whether the last statement of Q is K(y)>L
        If yes, output y and halts

$R$ generates $y$ where $|\braket{R,L}|=c+\log L$.

Complexity

Cell-Probe Model

Def [Bounds for complexity]. If we have found an algorithm with time (space) complexity $O(f(n))$ for a language $L$, $O(f(n))$ is an upper bound of the time (space) complexity for $L$; If we have proved that any algorithm for $L$ needs $\Omega (f(n))$ time (space), $\Omega (f(n))$ is a lower bound of the time (space) complexity for $L$.

“Were-you-last?” Game

Def. “Were-you-last?” Game:

$m$ players of Dream Team are taken to a game room one by one (they don’t know the order);
When a player leaves the game room, he is asked if he was the last of the $m$ players to go there and must answer correctly;
Inside the game room, there are many boxes. Every player can open at most $t$ boxes.
- He can put a pebble in an empty box or remove the pebble from a full box.
- He must close a box before opening the next one.
The Dream Team win if all players answer correctly. Assume there is their adversary, Hannibal, who knows their strategies, arranging the order of their entrance to the game room.

What is the smallest $t$ so that Dream Team has a winning strategy?

Rem. First try: $t=\Theta(\log_2m)$ is trivial. Just maintain a counter. Can we make $t$ smaller?

Thm. Dream Team has a winning strategy with $t=\Theta(\log\log m)$.

Pf. Represents the counter as “blocks” of 0s and 1s. Maintain:

type of last block number;
number of blocks;
size of each block.

Each entry above can be specified using $≤ \lceil \log\log m\rceil$bits. We only need to change blocks in the end. So

\[t≤7\lceil \log\log m\rceil +O(1). \]

The last problem is that how can the first player set the counter to $m$. Just assume you are always working on $C’=C\oplus m$, or using first $\log m$ players to set the counter to $m-\log m$.

Def. A sunflower is a collection of sets $S_1,…,S_p$ so that $S_i\cap S_j$ is the same for each pair of different sets $S_i$ and $S_j$.

Lem [Sunflower lemma]. Let $\mathcal{F}=\{S_1,…,S_m\}$ be a collection of sets each of cardinality $\le l$. If $m>(p-1)^{l+1} l!$, then the collection contains a sunflower with $p$ sets.

Pf. Induction on $l$: for $l=1$, $p$ sets of different single elements form a flower. For $l\ge 2$, take a maximal collection $A_1,…,A_t$ of pairwise disjoint members in $\mathcal{F}$.

If $t\ge p$, they form a flower with empty core.
If $t<p$, let $B=A_1\cup ...\cup A_t$, then $|B|\le (p-1)l$ and $B$ intersects every set in $\mathscr{F}.$

Thus some element $x\in B$ must be contained in

\[\ge \frac{(p-1)^{l+1}l!}{(p-1)l}=(p-1)^l(l-1)! \]
sets in $\mathscr{F}$. Delete $x$ from them, by induction hypothesis, these sets form a sunflower with $p$ sets. Add $x$ to them to get a sunflower in $\mathscr{F}$.

Thm. If $t ≤ 0.4 \log\log m$, the Dream Team lose.

Pf. Define $S_i$ to be the set of all bits that player $i$ may read/write. Then $|S_i|\le l= 2^t-1.$

When $t=0.4\log\log m$, we have $l<(\log m)^{0.4}$. Furthermore, let $p=2^l+1$,

\[(p-1)^{l+1}l!<(2^l)^{l+1}l^l=2^{l^2+l+l\log l}<m. \]

By Sunflower lemma, we can find a sunflower with $p>$ sets.

Hannibal first arrange other $m-p$ players, then these $p$ players. Clearly, only the center of the sunflower is meaningful for these players.

On the one hand, the possible number of status for the center is not greater than $2^l$. On the other hand, $p>2^l$, so there must be two players $i$ and $j$ will leave the same status. They cannot distinguish $1,...,i,i+1,...,j,j+1,...,p$ from $1,...,i,j+1,...,p$.

Rem. A simple counter needs $O(\log m)$ space and update time. Such a block counter needs $O(\log m\log\log m)$ space and $\Theta(\log\log m)$ update time.

Comparison-based Sorting

Def. Comparison-based sorting algorithm are algorithms that can only use comparison of pairs of elements to gain order information about a sequence.

Rem. A lower bound on the number of comparisons will be a lower bound on the complexity of any comparison-based sorting algorithm.

Thm. $\Omega(n \log n)$ is a lower bound of any comparison sort.

Pf. Consider a comparison-based sorting algorithm that enables to sort $n$ distinct numbers. The decision tree of this algorithm is a binary tree and has at least $n!$ leaf nodes, since there are $n!$ possible permutations. Thus the depth of the tree is $\ge \log_2(n!).$

By Stirling’s approximation, $$\log_2(n!)=\Theta(\log_2(\sqrt{2\pi n}\left(\frac{n}{e}\right)^n))=\Theta(n\log n).$$

Thus, the time lower bound for comparison-based sorting algorithm is $\Theta(n \log n)$.

Rem. The best worst-case complexity so far is $\Theta(n \log n)$ (merge sort and heapsort). Thus they are optimal under this model. In fact, we can beat the lower bound if we don’t base our sort on comparisons.

Information Retrieval Problem

Def. Cell probe model is a model of computation where the cost of a computation is measured by the total number of memory accesses to a random access memory. All other computations are not counted and are considered to be free.

Rem. Dynamic data structures:

Preprocessing phase: Given the input data, we can write in memory cells;
Update: The “input data” can be changed by a small amount each time;
Query phase: Determine whether a query datum is included in the input data.

Def. Information Retrieval Problem:

Input: a set $S$ of integers;
Query: an integer $x$, if $x\in S$?

Formally states, we want to minimize $\text{Cost}(\mathcal{T},\mathcal{S})$, which equals to the number of probes in the worst case with table structure $\mathcal{T}$ (how a particular set $S$ be placed in the table) and search strategy $\mathcal{S}$ (how to find a key $K$ in the table). Let $n=|S|,S\subseteq [M]$.

Def. Ramsey number $R(n_1,...,n_c)$ is the smallest number $n$ such that there exists cliques with color $i$ of size $n_i$ for some $i$, in all $K_n$ where every edge is colored with $c$ different colors.

Thm [Ramsey Theorem]. $R(n_1,...,n_c)$ exists for all $c,n_1,...,n_c\in\mathbb{N}$.

Pf. Prove the following statements.

$R(2,n)=R(n,2)=n$.
$R(r,s)\le R(r-1,s)+R(r,s-1).$
$R(n_1,...,n_c)\le R(n_1,...,n_{c-2},R(n_{c-1},n_c)).$

Lem. When $n\ge 2$ and $M\ge 2n-1$, if the table structure always stores keys in some fixed permutation, then $\lceil \log(n+1)\rceil$ probes are needed in worst-case for any search strategy.

Pf. Only need to prove the case that the table structure always stores keys in a sorted order. Consider the binary search structure.

Thm. For all $n$, there is an $N(n)$ such that we need $\lceil \log(n+1)\rceil$ probes for $M≥N(n)$.

Pf. Let $\mathcal{A}=\{S\subseteq [1,...,m]:|S|=n\}$. For all permutation $\sigma$, let

\[\mathcal{A}_{\sigma}=\{S=\{a_1<a_2<...<a_n\}\in A | S\text{ is stored as }(a_{\sigma(1)},a_{\sigma(2)},...,a_{\sigma(n)})\text{ in }\mathcal{T}\}. \]

By Ramsey theorem extension to hypergraph, when $M$ large enough, there is a subset $\Gamma\subseteq [1,..,M]$ and $|\Gamma|=2n-1$, such that $\exists \sigma,\forall S\subseteq \Gamma$ and $|S|=n$, $S\in \mathcal{A}_{\sigma}.$

By lemma, we need $\lceil \log(n+1)\rceil$ probes when all the elements are in $\Gamma$.

Rem. $\lceil \log(n+1)\rceil$ is also an upper bound. Sorted table & binary search gives it.

Dynamic Partial Sum

Def. Let $\mathbb{G}$ be a group. The dynamic partial sum problem asks to maintain an array $A[1,...,n]$ of group elements, under

$\text{UPDATE}(k,\Delta):$ modify $A[k]\leftarrow \Delta$, where $\Delta\in \mathbb{G}$;
$\text{SUM}(k):$ returns the partial sum $\sum\limits_{i=1}^k A[i].$

Assume $|\mathbb{G}|=2^{\delta}$and the word size for computer is $w\ge \log n$.

Thm [Pătraşcu, Demaine 2004]. Any data structure requires an average running time of $\Omega(\frac{\delta}{w}\log n)$ per updates and queries.

Pf. We design a “bad” sequence: Initially $A[1…n]=(0,…,0)$. Choose a random permutation $\pi\in S_n$ and a uniformly random sequence $\braket{\Delta_1,...,\Delta_n}\in\mathbb{G}^n.$ Do the following:

for t=1,2,...,n:
	UPDATE(𝜋(t),𝚫(t))
	SUM(𝜋(t))

Let $ IL(t_0, t_1, t_2)$ be the number of transitions between a value $\pi(i)$ with $i<t_1$, and a consecutive value $\pi(j)$ with $j>t_1$. Suppose $t_2-t_1=t_1-t_0=k$, we have

\[E[IL(t_0,t_1,t_2)]=\sum\limits_{j=1}^{2k-1}\text{Pr}[j\text{ is in }[t_0,t_1]]\text{Pr}[j+1\text{ is in }[t_1,t_2]]=\sum\limits_{j=1}^{2k-1}\frac{1}{2}\frac{k}{2k-1}=\frac{k}{2}. \]

Let $\Delta^*$ be the updates not in the range $[t_0,t_1]$, suppose it's fixed to some arbitrary $\mathbf{\Delta^*}$, then

\[H(\text{answers in }[t_1,t_2]|\Delta^*=\mathbf{\Delta^*})=\delta \cdot IL(t_0,t_1,t_2).\tag{1} \]

since the answers depend on $IL(t_0, t_1, t_2)$ independent random variables uniformly chosen from $\mathbb{G}$.

Let $IT(t_0,t_1,t_2)$ be the set of memory locations which

were read at a time $t_r\in[t_1,t_2]$;
were written at a time $t_w\in[t_0,t_1]$, and not overwritten during $[t_{w+1},t_r]$.

The above entropy is upper bounded by the average length of the information transfer encoding, which contains:

the cardinality $|IT(t_0, t_1, t_2)|$;
the address of each cell in $IT(t_0,t_1,t_2)$;
the contents of each cell at time $t_1$.

We have

\[H(\text{answers in }[t_1,t_2]|\Delta^*=\mathbf{\Delta^*})\le w+2wE_{\Delta}[|IT(t_0, t_1, t_2)|]\tag{2} \]

Combining (1) and (2) gives

\[E_{\Delta}[|IT(t_0, t_1, t_2)|]>\frac{\delta}{2w}IL(t_0,t_1,t_2)-1. \]

Finally, consider the total $IT$, which is the sum of all vertices of the segment tree:

\[\sum_{v}E[|IT(v)|]\ge\frac{\delta}{2w}\sum_v IL(v)-n\approx\frac{1}{4}n\log n. \]

Thus $$E[\sum_v|IT(v)|]=\Theta(\frac{\delta}{w}n\log n).$$

Rem. Proving lower bound: design a hard instance and analyze its information transfer

Rem. The upper bound given by segment tree meets the lower bound.

Deterministic & Nondeterministic

Time Complexity

Def (Time Complexity). Let $M$ be a deterministic Turing machine that halts on all inputs. The running time or time complexity of $M$ is the function $f: \mathbb{N}\to\mathbb{N}$, where $f(n)$ is the maximum number of steps that $M$ uses on any input of length $n$.

Def. $\mathsf{TIME}(t(n))$: all languages that are decidable by an $O(t(n))$ time deterministic Turing machine.

$\mathsf{NTIME}(t(n))$: all languages that are decidable by an $O(t(n))$ time nondeterministic Turing machine.

Def.

\[\mathsf{P}=\bigcup_k\mathsf{TIME}(n^k),\mathsf{NP}=\bigcup_k\mathsf{NTIME}(n^k),\mathsf{EXP}=\bigcup_k\mathsf{TIME}(2^{n^k}),\mathsf{NEXP}=\bigcup_k\mathsf{NTIME}(2^{n^k}). \]

The Church-Turing thesis says all these models, e.g., Turing Machine and java, are equivalent in power... but not in running time!

Cobham-Edmonds thesis. For any realistic models of computation $M_1$ and $M_2$, $M_1$ can be simulated on $M_2$ with at most polynomial slowdown.

Rem. Quantum computation does NOT change the Church-Turing thesis, that is, what is computable. But it does seem to change what is computable in polynomial time.

Space Complexity

Def (Space Complexity Classes). For any function $f: \mathbb{N}\to\mathbb{N}$, we define

\[\mathsf{SPACE}(f(n))=\{ L : L\text{ is decidable by deterministic TM }M\text{ which scans }O(f(n))\text{ tape cells.}\}\\ \mathsf{NSPACE}(f(n))=\{ L : L\text{ is decidable by non-deterministic TM }M\text{ which scans }O(f(n))\text{ tape cells on any branch of its computation.}\} \]

Rem. Here we consider 3-tape machines:

Input tape is read-only
Work tape can read and write
Output tape is write-only.

Only the size of the work tape is counted for complexity purposes.

Ex. $\mathsf{SAT}\in\mathsf{SPACE}(n)$.

Logarithmic Space

Def (Logarithmic Space Classes).

\[\mathsf{L} = \mathsf{SPACE}(\log n),\mathsf{NL} = \mathsf{NSPACE}(\log n). \]

Fact.

$\mathsf{TIME}(f(n))\subseteq\mathsf{SPACE}(f(n)).$

Since a machine that uses $f(n)$ time can use at most $f(n)$ space.
$\mathsf{SPACE}(f(n))\subseteq\mathsf{TIME}(2^{O(f(n))}).$

A machine uses $O(f(n))$ space can have at most $2^{O(f(n))}$ configurations. A TM that halts may not repeat a configuration, so the total time to “list” all configurations is $f(n)\cdot 2^{O(f(n))} = 2^{O(f(n))}$.
$\mathsf{NTIME}(f(n))\subseteq\mathsf{SPACE}(f(n)).$

We can enumerate all possible $O(f(n))$ “guesses” (of size $O(f(n))$) in $O(f(n))$ space.

$\mathsf{NSPACE}(f(n))\subseteq\mathsf{TIME}(2^{O(f(n))}).$

Construct the configuration graph with $2^{O(f(n))}$ vertices. Check whether accepting configurations are reachable from start configuration.

Thm. The following inclusions hold:

\[\mathsf{L\subseteq NL\subseteq P\subseteq NP\subseteq PSPACE\subseteq NPSPACE\subseteq EXPTIME} \]

NL-completeness

Def (Log-Space Reductions). $A$ is log-space reducible to $B$, written $A \leq_L B$, if there exists a log space TM M that, given input $w$, outputs $f(w)$ s.t. $w \in A$ iff $f(w) \in B$.

Thm. If $A_1\le_L A_2$ and $A_2\in \mathsf{L}$, then $A_1\in \mathsf{L}$.

Pf. Let $M$ be a TM for $A_2$. On input $x$, simulate $M$ on $f(x)$ and whenever $M$ need to read the $i^{\text{th}}$ bit of $x$, run $f$ on $x$ to send the $i^{\text{th}}$ of $f(x)$ to $M$. Since $i$ is bounded by $\text{poly}(n)$, record it only takes $O(\log n)$ bit.

Thm. More generally, if $f$ and $g$ are log-space computable functions, $f \circ g$ is also log-space computable.

Pf. First we can see $g'(x, i)$, the $i^{\text{th}}$ bit of $g(x)$, is computable in log-space. We just wait until the $i^{\text{th}}$ bit comes out. Size of $g(x)$ polynomial of $|x|$, so size of $i$ is $O(\log |x|)$. To compute $f(g(x))$, directly simulate the function $f$, whenever $f$ reads the $i^{\text{th}}$ bit on $g(x)$, call $g'(x, i)$.

OPEN PROLEM. Is NP-Completeness closed under log-space reduction?

Def (NL-Completeness). A language $B$ is $\mathsf{NL}$-hard if for every $A\in\mathsf{NL}, A\leq_LB$. A language $B$ is $\mathsf{NL}$-Complete if $B∈\mathsf{NL}$ and $B$ is $\mathsf{NL}$-hard.
Ex. PATH (st-connectivity):

Instance: A directed graph $G$ and two vertices $s,t\in V$
Problem: To decide if there is a path from $s$ to $t$ in $G$

First, the following machine decides PATH so immediately PATH $\in\mathsf{NL}$:

Start at s
for i = 1, ..., |V|:
	Non-deterministically choose a neighbor and jump to it
	if you get to t:
    	return accept
return reject

Then we can show that PATH is $\mathsf{NL}$-Complete by reduction. Any $\mathsf{NL}$ language $A$, assume $M$ is a NTM that decides $A$. For the computation of $M$ on an input $x$, it can be described by a graph $G_{M,x}$:

Each vertex corresponds to a configurations of $M$
$(u,v)\in E$ if $M$ can move from $u$ to $v$ in one step
$s$ corresponds to the start configuration, $t$ corresponds to the accept configuration (w.l.o.g., we can assume all NTM’s have exactly one accepting configuration)

Clearly, $M$ accepts $x$ iff there is a path from $s$ to $t$ in $G_{M,x}$. Also this graph is log-space computable from $M,x$. So we have a log-space reduction from $A$ to PATH. Thus PATH is $\mathsf{NL}$-Complete. Since PATH is $\mathsf{P}$, immediately we have:

Prop. $\mathsf{NL}\subseteq\textsf{P}$.

Thm (Savitch's Theorem). $\textsf{NL}\subseteq\mathsf{SPACE}(\log^2n).$

Pf. Only need to show PATH $\in\mathsf{SPACE}(\log^2n)$.

bool PATH(a,b,d) { //whether there is path from a to b with distance ≤d
    if there is an edge from a to b then 
    	return TRUE
    else {
        if d=1 return FALSE
        for every vertex v { 
            if PATH(a,v, ⎣d/2⎦) and PATH(v,b, ⎡d/2⎤) then
            	return TRUE
        } 
        return FALSE
    }
}

In the above algorithm, we need to maintain a recursion stack. In this stack, each call takes $O(\log n)$ space (to keep track of $v$ and $d$), and $O(\log n)$ recursion depth, so $O(\log^2 n)$ space in total. Thus PATH can be decided by a deterministic TM in $O(\log^2n)$ space.

Rem. For undirected version (USTCON), it's $\mathsf{L}$. [Reingold, STOC'05]

Ex. NON-PATH:

Instance: A directed graph $G$ and two vertices $s,t∈V$
Problem: To decide if there is no path from $s$ to $t$

Clearly, NON-PATH is $\mathsf{coNL}$-Complete.

Thm [Immerman/Szelepcsenyi, 1987].

\[\mathsf{NL=coNL}. \]

Pf. Let's prove it by showing NON-PATH is $\mathsf{NL}$. Consider the following machine :


bool NON_PATH(G, s, t):
	count ← 1
    for l ← 1 to n:
		count ← Number_of_Reachable_Vertices(s, l, count)
    if R(s, t, n, count) == 1:
		return false
	return true

The next question is how to count the number of reachable vertices. Here is a log-space nondeterministic algorithm for it:

int Is_v_reachable(s, v, l, count):
	for each u ≠ v:
 		b ← guess if u is reachable from s in l steps
 		newcount ← newcount + b
 		if b = 1:
 			guess a path from s to u of length ≤ l
			if we don’t reach u:
				return reject
     if newcount == count:
		return 0
     if newcount == count - 1:
         guess a path to v
         if we find it:
			return 1 
         else:
			return reject
     else:
		return reject

int Number_of_Reachable_Vertices(s, l, bef):
	aft ← 0
        for each v:
            for each u:
				if (u, v) ∈ E and R(s, u, l-1, bef):
					aft = aft + 1
                    break
 	return aft

Polynomial Time/Space

Padding Argument

Thm. If $\mathsf{P=NP}$, then $\mathsf{EXP=NEXP}$.

Pf. We need to show $\mathsf{NEXP\subseteq EXP}$. For a language $L\in\mathsf{ NEXP}$, we know there is some NTM $M$ decides $L$ in $2^{n^c}$time. Let

\[L'=\left\{x1^{2^{|x|^c}}\Big|x\in L\right\} \]

where $1$ is a symbol not in $L$. Clearly, $L'$ can be decides by a polynomial time NTM. By assumption, $L'\in\mathsf{P}$. Thus $L\in\mathsf{EXP}$.

Rem. This proof technique is called padding argument.

Exploit it, we can generalize Savitch's Theorem.

Def. A function $f:\mathbb{N\to N}$, where $f(n) \ge \log n$, is called space constructible, if the function that maps $1^n$ to the binary representation of $f(n)$ is computable in space $O(f(n))$.

A function $f:\mathbb{N\to N}$, where $f(n) \ge n\log n$, is called time constructible, if the function that maps $1^n$ to the binary representation of $f(n)$ is computable in time $O(f(n))$.

Thm. For any space constructible function $S(n)\ge \log (n)$,

\[\mathsf{NSPACE}(S(n))\subseteq\mathsf{SPACE}(S(n)^2). \]

Pf. Apply padding argument on $\textsf{NL}\subseteq\mathsf{SPACE}(\log^2n)$:

For $L\in\mathsf{NSPACE}(S(n))$, suppose NTM $N$ decides $L$, let

\[L'=\left\{x\#0^{2^{S(|x|)}}\Big|x\in L\right\}. \]

Construct the following TM $N'$:

Count backwards the number of 0's and check there are 2^S(|x|) such
Run M_L on x

We can see that $N'$ decides $L'$ in $O(S(|x|))$ space. Thus $L'\in \mathsf{NL}\subseteq \mathsf{SPACE}(\log^2n).$ Immediately, there is a DTM $D'$ decides $L'$ in $O(\log^2 n)=O(S(n)^2)$ space. Since $f:x\to x\#0^{2^{S(|x|)}}$ can be computed in $O(S(|x|))$ space, we derive $L\in \mathsf{SPACE}(S(n)^2)$.

Cor.

\[\mathsf{PSPACE=NPSPACE}. \]

Pf. Clearly, $\mathsf{PSPACE\subseteq NPSPACE}$. By Savitch's theorem, $\mathsf{NPSPACE\subseteq PSPACE}$.

Cor. For any space constructible function $S(n)\ge \log (n)$,

\[\mathsf{NSPACE}(S(n))=\mathsf{coNSPACE}(S(n)). \]

Pf. Apply padding argument on $\textsf{NL=coNL}$.

PSPACE-completeness

Def. A language $B$ is $\mathsf{PSPACE}$-hard if for every $A \in \mathsf{PSPACE}$, $A \leq_p B$. A language $B$ is $\mathsf{PSPACE}$-Complete if $B \in \mathsf{PSPACE}$ and $B$ is $\mathsf{PSPACE}$-hard.

Ex. TQBF (true quantified Boolean formula):

Instance: A fully quantified Boolean formula $\phi$ (can be written in prenex form)
Problem: To decide if $\phi$ is true

First, let's show TQBF $\in\mathsf{PSPACE}$. We'll describe a poly-space algorithm $A$ for evaluating $\phi$:

A:
	If 𝜙 has no quantifiers: evaluate it
	If 𝜙=∀x(𝜓(x)):
		call A on 𝜓(0) and on 𝜓(1)
        Accept if both are true
	If 𝜙=∃x(𝜓(x)):
		call A on 𝜓(0) and on 𝜓(1)
        Accept if either are true

The total space needed is polynomial in the number of variables (the depth of the recursion).

Next, show TQBF is $\mathsf{PSPACE}$-hard:

Given a poly-space TM $M$ for a language $L \in \mathsf{PSPACE}$, and an input $x$, we construct a QBF $\psi$ of polynomial size s.t. $\psi$ is true iff $M$ accepts $x$.

In the TM $M$ for configurations $u, v$ and an integer $t$, define $\psi(u, v, t) = \text{true}$ iff $v$ is reachable from $u$ within $t$ steps

$\psi(u, v, 1)$ is efficiently computable
For $t > 1$,

\[\begin{align*} \psi(u, v, t) =&\ (\exists m)(\forall (a,b)\in\{(u,m),(m,v)\})\psi(a,b, t/2)\\ =&\ (\exists m)(\forall a)(\forall b) [((a=u \wedge b=m)\vee (a=m\wedge b=v))\to \psi(a, b, t/2)] \end{align*} \]
where $m$ is another configuration.

Let $S(t)$ be the size of $\psi(u,v,t)$. Then

\[S(t)=S(t/2)+\text{poly}(|x|)=\text{poly}(|x|\log t)=\text{poly}(|x|) \]

since $\mathsf{PSPACE\subseteq EXPTIME}$ so $\log t=O(|x|)$.

We can see that $M$ accepts $x$ iff $\psi_{M,x}=\psi(c_{\text{start}},c_{\text{accept}},h)$ is true. Since $\psi$ is constructible in poly-time, any $\mathsf{PSPACE}$ language is poly-time reducible to TQBF. So far, TQBF is $\mathsf{PSPACE}$-Complete.

Ex. Formula Game: The game contains two players $A$ and $E$, with a Boolean formula $\psi$ with variables $x_1 ,x_2 ,...,x_n$. They will play alternately: $A$ selects the value of $x_1$, $E$ selects the value of $x_2$, $A$ selects the value of $x_3$, $E$ selects the value of $x_4$... Finally, $A$ wins if $\psi$ is false, $E$ wins if $\psi$ is true.

We can see that $E$ has winning strategy iff

\[(\forall x_1)(\exists x_2)(\forall x_2)(\exists x_4)...[\psi] \]

is true, which is in the form of TQBF.

In fact, the Formula Game is $\mathsf{PSPACE}$-complete even if $\psi$ is a 3-CNF. Since for any $\psi(x)$, we can find a 3-CNF $\phi(x,y)$ s.t. $\psi(x)$ is true iff $(\exists y)\phi(x,y)$ is true.

Ex. Generalized geography game:
In a directed graph with a start node $s$: Initially token is at $s$. Player 1 and 2 alternatively choose the next node, if the token is currently at $v$, it can choose $w$ if $(v, w)$ is an edge. No repetition is allowed. When a player cannot move on, it loses. Who has a winning strategy here?

$\text{GG} = {\langle G, b \rangle \mid \text{Player 1 has a winning strategy for the Generalized Geography game played on graph } G \text{ starting at node } b }.$

Clearly, $\text{GG}$ is in $\mathsf{PSPACE}$. And we can reduce the Formula Game for 3CNF to GG game as follows:

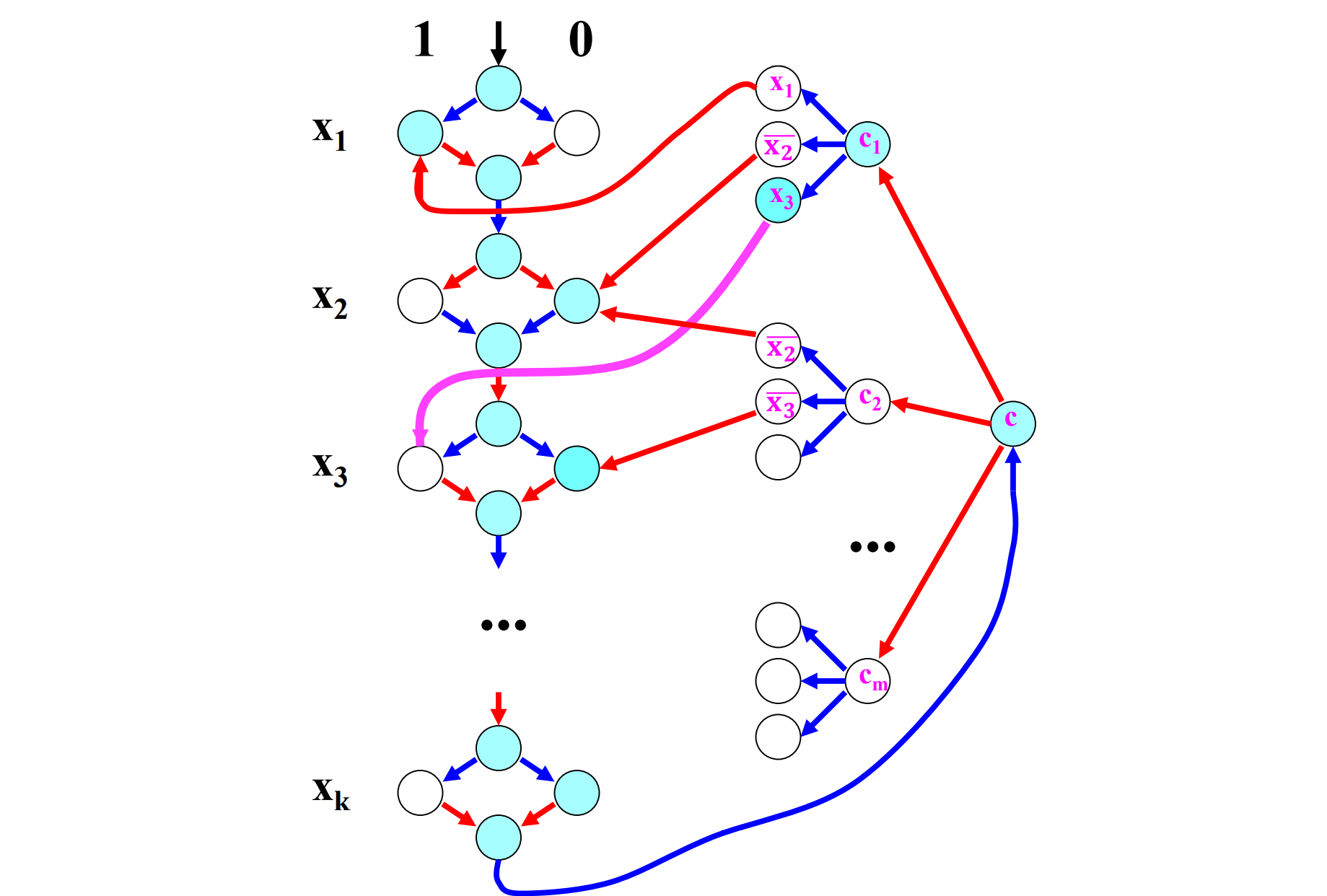
Thus GG is also $\mathsf{PSPACE}$-complete.

Ex. Gomoku (five-in-a-row): Players alternate turns placing a stone of their color on an empty intersection. Black plays first. The winner is the first player to form an unbroken line of five stones of their color horizontally, vertically, or diagonally.

Gomoku is also $\mathsf{PSPACE}$-complete. [Stefan Reisch, 1980]

Lem. If $M(x)$ takes $f(|x|)$ time, to simulate $M$ on a universal TM takes $\Theta(f(|x|)\log f(|x|))$ steps.

Thm (Time Hierarchy Theorem). For any time constructible function $f: \mathbb{N} \rightarrow \mathbb{N}$, there exists a language $\mathcal{L}$ that is decidable in time $O(f(n))$, but not in

\[o\left(\frac{f(n)}{\log f(n)}\right) \]

Pf. Consider following TM:

D(<M>):
	Simulate M with input <M> for c⋅f(n=|<M>|) steps;
	if accepts then reject;
	else accept;

We know that $L(D)$ is in $\mathsf{TIME}(f(n))$. Suppose $L(D)$ is in $\mathsf{TIME}\left(\frac{f(n)}{\log f(n)}\right)$, that is, there is a machine $M'$ deciding $L(D)$ in $O\left(\frac{f(n)}{\log f(n)}\right)$ time. Consider $D(\langle M'\rangle)=M'(\langle M'\rangle)$. We can make $|\langle M'\rangle|$ not too small and $c$ large enough, so the simulation can finish in $cf(n)$ steps, leads to a contradiction with $D(\langle M'\rangle)=M'(\langle M'\rangle)$.

Thm (Space Hierarchy Theorem). For any space constructible function $f: \mathbb{N} \rightarrow \mathbb{N}$, there exists a language $\mathcal{L}$ that is decidable in space $O(f(n))$, but not in space $o(f(n))$

Cor. If $f(n)$ and $g(n)$ are space constructible functions, and $f(n)=o(g(n))$, then $\mathsf{SPACE}(f) \varsubsetneqq \mathsf{SPACE}(g)$.

Polynomial-Time Hierarchy

In $\mathsf{NP}$, most problems are either in $\mathsf{P}$ or in $\mathsf{NP}$-Complete. Also, there are some problems we don't know whether they are in $\mathsf{P}$ or in $\mathsf{NP}$-Complete.

Bold conjecture: every problem of $\mathsf{NP}$ is either in $\mathsf{P}$ or $\mathsf{NP}$-Complete?

Thm (Ladner 1975). Suppose that $\mathsf{P} \neq \mathsf{NP}$, then there exists $\mathsf{NP}$-intermediate problems (in $\mathsf{NP} \setminus \mathsf{P}$ and not $\mathsf{NP}$-Complete).

Pf. Define $M_i$ to be the TM with code $i$. Add a clock to $M_i$ so that it runs in at most $n^i$ steps (If it doesn't terminate after $n^i$ steps, just reject). So we can enumerate (TMs deciding) all languages in $\mathsf{P}$ by enumerating all polynomial time machines.

Similarly, we can also enumerate all $\mathsf{NP}$-hard languages: Enumerate TMs $f_i$ computing all polynomial-time functions in $n^i$ steps, then the NTM $N_i$ that decides the language which SAT reduces to via $f_i$ as the reduction virtually exists. So we can also enumerate all languages that is $\mathsf{NP}$-hard.

Now let's construct $A\in\mathsf{NP}$ that is neither in $\mathsf{P}$ nor $\mathsf{NP}$-hard. Recall that $\{M_i\}$ enumerate $\mathsf{P}$ and $\{N_i\}$ enumerate $\mathsf{NP}$-hard.

For any $M_i$ and any $x$, we can always find some $z\ge x$ on which $M_i$ and SAT differ. (Otherwise SAT is in $\mathsf{P}$.)
For any $N_i$ and any $x$, we can always find some $z\ge x$ on which $M_i$ and TRIV differ. (TRIV $=\emptyset$)

Let $g(n)$ be a carefully constructed function. Consider a language $A=\{x|x\in\text{SAT and }g(|x|)\text{ is even}\}$, in other words,

If $g(|x|)$ is even, $A(x)=\text{SAT}(x)$.
If $g(|x|)$ is odd, $A(x)=\text{TRIV}(x)$.

Our aim: all $M_i$ and $N_i$ doesn’t decide $A$ and $A\in\mathsf{NP}$. Let $g(0)=g(1)=2$. If $\log^{g(n)}n\ge n$ then let $g(n+1)=g(n)$, otherwise:

If $g(n)=2i$: Find $z$ s.t. $|z|<\log n$, $g(|z|)$ even and $\text{SAT}(z)\neq M_i(z)$. If found, $g(n+1)=g(n)+1$; otherwise, $g(n+1)=g(n)$.
If $g(n)=2i+1$: Find $z$ s.t. $|z|<\log n$, either
- $g(|f_i(z)|)$ is odd and $z\in\text{SAT}$, so $f_i(z)\in L(N_i)$ but $f_i(z)\notin A$.
- $g(|f_i(z)|)$ is even and $\text{SAT}(z)\neq \text{SAT}(f_i(z))$, so $N_i(f_i(z))\neq A(f_i(z))$.
If found, $g(n+1)=g(n)+1$; otherwise, $g(n+1)=g(n)$.

Clearly, $g$ can be computed in polynomial time so $A\in\mathsf{NP}$. Besides, all $M_i$ and $N_i$ doesn’t decide $A$.

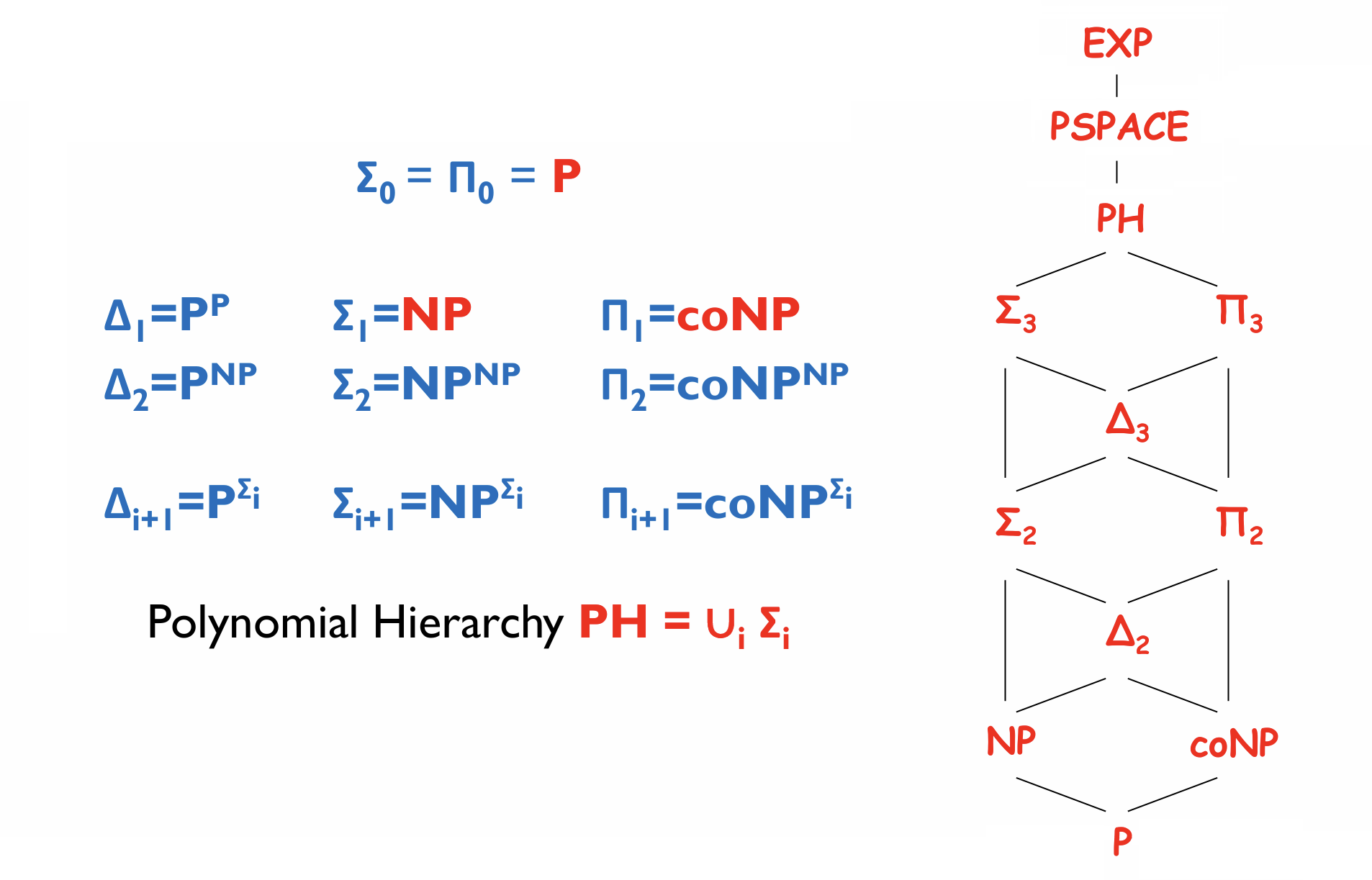
Def (Polynomial Hierarchy). For $i\ge 1$, a language $L$ is in $\Sigma_i^p$ if there exists a polynomial time TM $M$ and a polynomial $q$ s.t.

\[x \in L \Leftrightarrow \exists u_1 \in \{0,1\}^{q(|x|)} \forall u_2 \in \{0,1\}^{q(|x|)} \ldots Q_i u_i \in \{0,1\}^{q(|x|)} M(x, u_1, \ldots, u_i)=1 \]

where $Q_i$ is $\exists$ when $i$ is odd; is $\forall$ when $i$ is even. (sometimes we can omit superscript "$p$"). Define $\mathsf{PH}=\bigcup_i\Sigma_i^p$.

Symmetrically, $\Pi_i^p=\mathsf{co}-\Sigma_i^p$: for $i\ge 1$, a language $L$ is in $\Pi_i^p$ if there exists a polynomial time TM $M$ and a polynomial $q$ s.t.

\[x \in L \Leftrightarrow \forall u_1 \in \{0,1\}^{q(|x|)} \exists u_2 \in \{0,1\}^{q(|x|)} \ldots Q_i u_i \in \{0,1\}^{q(|x|)} M(x, u_1, \ldots, u_i)=1 \]

where $Q_i$ is $\forall$ when $i$ is odd; is $\exists$ when $i$ is even.

Ex. $\Sigma_0^p=\mathsf{P},\Sigma_1^p=\mathsf{NP}$.

Fact.

$\mathsf{PH}=\bigcup_i\Pi_i^p$ since $\Sigma_i^p\subseteq\Pi_{i+1}^p\subseteq\Sigma_{i+2}^p$.
$\mathsf{PH\subseteq PSPACE}$.

We can define it by oracle Turing machines. Shorthand:

Let $\mathsf{C}$ be a complexity class and $A$ be a language. Define

\[\mathsf{C}^A=\{L\text{ decided by OTM }M\text{ with oracle }A\text{ with }M\text{ ``in'' }\mathsf{C}\} \]
Let $\mathsf{C}$ be a complexity class and $M$ be a OTM. Define

\[M^{\mathsf{C}}=\{L\text{ decided by OTM }M\text{ with oracle }A\text{ with }A\in C\} \]
Both together: Let $\mathsf{C,D}$ be complexity classes. Define

\[\mathsf{C}^{\mathsf{D}}=\{L\text{ decided by OTM ``in'' }\mathsf{C}\text{ with oracle language from } \mathsf{D}\} \]

Ex. $\Sigma_2=\mathsf{NP}^{\mathsf{NP}},\Pi_2=\mathsf{coNP}^{\mathsf{NP}}$.

Thm (Collapse of hierarchy). If $\mathsf{P=NP}$, then $\mathsf{PH=P}$, that is, the hierarchy collapses to $\mathsf{P}$.

Pf. Assume $\Sigma_1^P=\mathsf{NP=P}$, let's prove $\Sigma_i^p=\mathsf{P}$ by induction on $i$.

Suppose $\Sigma_{i-1}^p=\mathsf{P}$, we will show $\Sigma_i^p=\mathsf{P}$. For a language in $\Sigma_i^p$:

\[x\in L\Leftrightarrow\exists u_1\in\{0,1\}^{q(|x|)}\forall u_2\in\{0,1\}^{q(|x|)}...Q_i u_i\in\{0,1\}^{q(|x|)}M(x,u_1,...,u_i)=1. \]

Define $L'$:

\[(x,u_1)\in L'\Leftrightarrow\forall u_2\in\{0,1\}^{q(|x|)}...Q_i u_i\in\{0,1\}^{q(|x|)}M(x,u_1,...,u_i)=1. \]

Then $L'\in\Pi_{i-1}^p=\text{co}\Sigma_{i-1}^p=\mathsf{P}$. Since $x\in L\Leftrightarrow \exists u_1\in\{0,1\}^{q(|x|)}[(x,u_1)\in L']$, $L\in\mathsf{NP=P}$.

Rem. Similarly, if $\Sigma_i^p=\Pi_i^p$, $\mathsf{PH}=\Sigma_i^p.$

Relativization

Many proofs and techniques we have seen are relativize: they hold after replacing all TMs with oracle TMs that have access to an oracle $A$. (including diagonalization). e.g. $\mathsf{L}^A \subseteq \mathsf{P}^{A}$ for all oracles $A$, and $\mathsf{P}^{A} \neq \mathsf{EXP}^{A}$ for all oracles $A$.

Can we solve $\mathsf{P}\text{ v.s. }\mathsf{NP}$ using such kind of proof?

Thm (Baker, Gill, and Solovay, 1975). There exists

oracle $A$ for which $\mathsf{P}^A = \mathsf{NP}^A$;
oracle $B$ for which $\mathsf{P}^B \neq \mathsf{NP}^B$.

Pf. For $\mathsf{P}^A = \mathsf{NP}^A$, need $A$ to be powerful. $A=\text{TQBF}$ works, since

\[\mathsf{PSPACE}\subseteq\mathsf{P}^{\text{TQBF}}\subseteq\mathsf{NP}^{\text{TQBF}}\subseteq\mathsf{NPSPACE} \]

and we know $\mathsf{PSPACE=NPSPACE}.$

For $\mathsf{P}^B \neq \mathsf{NP}^B$, define another language that depends on $B$:

\[L(B)=\{1^k:\exists x\in B\text{ s.t. }|x|=k\}. \]

Obviously, $L(B)\in\mathsf{NP}^B$ whatever $B$ is. We will find a language $B$ s.t. $L(B)\notin\mathsf{P}^B$. Consider following process:

Initially, $B,X=\emptyset$. ($X$ is used to collect strings that are excluded from $B$, so $B\cap X=\emptyset$.)
At stage $i$, let $M_i$ be the $\left(i-\lfloor\sqrt{i}\rfloor^2\right)$-th deterministic OTMs:
- select $n$ so that $n>|x|$ for all $x \in B$ and $x \in X$ currently
- simulate $M_i\left(1^n\right)$ for $n^{\log n}$ steps
- when $M_i$ makes an oracle query $q$:
  - if $|q|<n$, answer using $B$
  - if $|q| \geq n$, answer "no"; add $q$ to $X$
- if simulated $M_i$ accepts $1^n$, add all $\left\{0, 1\right\}^n$ to $X$ (so $1^n \notin L(B)$)
- if simulated $M_i$ rejects $1^n$, add $\left\{0, 1\right\}^n \backslash X$ to $B$

Therefore, $L(B)\notin\mathsf{TIME}(n^{\log n})^B$, so $L(B)\notin \mathsf{P}^B$.

Rem. This theorem tells us that resolving $\mathsf{P}\text{ v.s. }\mathsf{NP}$ requires a non-relativizing proof.

Exponential Time

Def (Alternating Turing machines). An alternating Turing machine is a nondeterministic TM with an additional feature. Its states, except for the accept and reject states, are divided into universal states and existential states. When we run an alternating TM on an input string, we label each node of its nondeterministic computation tree with $\wedge$ or $\vee$, depending on whether the corresponding configuration contains a universal or existential state. We determine acceptance by designating a node to be accepting if it is labeled with $\wedge$ and all of its children are accepting or if it is labeled with $\vee$ and at least one of its children is accepting.

Def. We can define classes of languages that are decided by certain alternating TM:

\[\mathsf{ATIME}(t(n))=\{L\mid L\text{ is decided by an }O(t(n))\text{ time alternating TM}\}\\ \mathsf{ASPACE}(t(n))=\{L\mid L\text{ is decided by an }O(t(n))\text{ space alternating TM}\} \]

Claim. For $f(n)\ge n$, $\mathsf{ATIME}(f(n)) \subseteq \mathsf{SPACE}(f(n))$.

Pf. Do a DFS to explore all possible branches.

Claim. For $f(n)\ge n$, $\mathsf{SPACE}(f(n)) \subseteq \mathsf{ATIME}(f(n)^2)$.

Pf. In the TM $M$, For configurations $u, v$ and an integer $t$, define $\psi(u, v, t)=\text{true}$ iff $v$ is reachable from $u$ within $t$ steps. For $t>1$,

\[\psi(u, v, t)=(\exists m)[\psi(u, m, t/2) \land \psi(m,v,t/2)]=(\exists m)(\forall (a,b)\in\{(u,m),(m,v)\})[\psi(a,b, t/2)] \]

So the depth of the recursion is $\log 2^{O(f(n))}=O(f(n))$, and generating each configuration $m$ takes $O(f(n))$ time, so the total time is $O(f(n)^2)$.

Claim. For $f(n) \ge \log n$, $\mathsf{ASPACE}(f(n))=\mathsf{TIME}(2^{O(f(n))})$.

Pf. $\mathsf{ASPACE}(f(n))\subseteq\mathsf{TIME}(2^{O(f(n))})$: Since the space is $O(f(n))$, the number of all configurations is $2^{O(f(n))}$, simply enumerate all the possible configurations and construct the computation tree.

$\mathsf{TIME}(2^{O(f(n))})\subseteq\mathsf{ASPACE}(f(n))$: For a machine takes $2^{O(f(n))}$ time, consider the table for computation history. Let $C[i,j]$ denote the $j$-th cell in time $i$ in the configuration table. Notice that $C[i,j]$ only depends on $C[i-1,j-1],C[i-1,j],C[i-1,j+1]$. So we can construct the following algorithm:

Guess(i, j, d) {	\\Guess the C[i,j]=d
    for all (a, b, c) that can yield d {  
      if all of 
          Guess(i-1, j-1, a),  
          Guess(i-1, j, b),  
          Guess(i-1, j+1, c)   
      are true, return true;  
	}  
	return false;
}

Finally, we can check $\text{Guess}(n, j, q_{\text{accept}})$ for all cell $j$ in the final time $n$. We only need to store the pointer, i.e., $i,j,d$, so the space is $\log 2^{O(f(n))}=O(f(n)).$

Thm (Stockmeyer & Chandra 1979). Variants of Boolean formula games which are closer to board games are $\mathsf{EXPTIME}$-Complete. For example, Game 1:

Given a Boolean formula $\psi(x_1,...,x_m,y_1,...,y_m,t)(\psi(X,Y,t))$. Each time player 1 set $t=1$ and set $x_1,…, x_m(X)$ to any values, and player 2 set $t=0$ and set $y_1,…, y_m (Y)$ to any values. Player 1 moves first, no pass. A player loses if $\psi$ is false after its move. Let $\alpha$ be the initial value for $Y$.

Pf. Recall that $\mathsf{APSPACE=EXPTIME}$. We only need to show that Game 1 is in $\mathsf{APSPACE}$-Complete. Suppose $M$ is an alternating TM in polynomial space, w.l.o.g.,

The initial state is existential.
Existential states yield universal states, and universal states yield existential states.
Accepting states are universal, and rejecting states are existential.

Consider the configurations of $M$ with length polynomial in $n$. Define $\text{NEXT}(C, D)$ where $C, D$ are configurations of $M$:

When $C \vdash_M D$, $\text{NEXT}(C, D) = 1$.
If $C$ is an accepting/rejecting configuration, $\text{NEXT}(C, D) = 0$ for all $D$.

Construct a Boolean formula as

\[\psi = (\neg t \vee \text{NEXT}(Y, X)) \wedge (t \vee \text{NEXT}(X, Y)) \]

and let $\alpha$ be the initial configuration of $M$ on input $w$. In Game 1, player 1 sets $t = 1$ and chooses $X$, then $\psi = \text{NEXT}(Y, X)$; player 2 sets $t = 0$ and chooses $Y$, then $\psi = \text{NEXT}(X, Y)$. So Player 1 is always in existential states, and Player 2 is always in universal states. Every player aims to select a halting configuration: Player 1 aims to select an accepting state; Player 2 aims to select a rejecting state.

Therefore, Player 1 wins if and only if $M$ accepts $w$.

We can reduce Game 1 to other games.

Thm (Fraenkel & Lichtenstein, 1981). $n\times n$ chess is $\mathsf{EXPTIME}$-Complete.

Thm (J. M. Robson, 1984). $n\times n$ checkers is $\mathsf{EXPTIME}$-Complete.

Def. A pebble game is a quadruple $G = (X, R, S, t)$ where:

$X$ is a finite set of nodes;
$R \subseteq \{(x, y, z): x, y, z \text{ are distinct elements in } X\}$ is set of rules;
$S \subseteq X$ is the places of initial pebbles;
$t \in X$ is the terminal node.

Two players play the game. They alternatively move pebbles using any rule in $R$. Let $A$ be the current places of pebbles, if $(x, y, z) \in R$ is a rule, and $x, y \in A$ but $z \notin A$, then the player can turn $A$ into $(A-\{x\}) \cup \{z\}$ in one turn. The winner is the first player who can put a pebble on the terminal node, or who can make the other player unable to move.

Thm (Kasai, Adachi, Iwata, 1978) . 2-person “pebble game” is $\mathsf{EXPTIME}$-Complete.

Pf. Reduction from $\mathsf{APSPACE}$ to this pebble game. In alternating TM, if $\delta(q, a)$ contains $(q', a', d)$ where $q, q'$ are states, $a, a'$ are tape symbols, $d= \pm 1$ is direction, make nodes in pebble game:

\[[q,l],[l,a],[q,l,a,a'],[l,a'],[q',l+d] \]

and rules:

\[([q, l], [l, a], [q,l, a, a']),\\ ([l, a], [q,l, a, a'],[l,a']),\\ ([q,l,a,a'],[l,a'],[q',l+d]). \]

Def. Succinct circuit SAT: given $i$ and $k$, a circuit outputs the index and type of the $k$-th adjacent gate of the $i$-th gate. input/output of length $n$, polynomial circuit size.

Thm. Succinct circuit SAT is $\mathsf{NEXP}$-complete.

Pf. As in the proof of $\mathsf{NP}$-completeness of SAT, we can use a poly-size circuit to generate that formula:

\[\varphi_{M,w}=\phi_{\text{cell}}\wedge\phi_{\text{start}}\wedge\phi_{\text{move}}\wedge\phi_{\text{accept}}. \]

Thm. Go with Japanese ko rule is $\mathsf{EXPTIME}$-Complete.

Thm. Minesweeper is $\mathsf{NP}$-Complete.

Randomized Computation

Probabilistic TM

Def (Probabilistic Turing Machine). Deterministic TM with additional read-only tape containing “coin flips”. Formally, there are (at least) three tapes:

$1^{\text{st}}$ Tape holds the input;
$2^{\text{nd}}$ Tape (also known as the random tape) is covered randomly (and independently) with 0’s and 1’s, with $\frac{1}{2}$ probability of a $0$ and $\frac{1}{2}$ probability of a $1$;
$3^{\text{rd}}$ Tape is used as the working tape.

Def (Monte Carlo). A Monte Carlo algorithm is a randomized algorithm whose running time is deterministic, but whose output may be incorrect with a certain (typically small) probability.

Def (Las Vegas). A Las Vegas algorithm is a randomized algorithm that always gives correct results; it gambles only with the resources used for the computation.

Additive Spanner

Def. A $c$-additive spanner $S$ in $G$ is a spanning subgraph of $G$ which satisfies two crucial properties:

sparse;
for all $u, v \in G$, $d_S(u, v) \leq d_G(u, v) + c$.

Here we consider undirected unweighted graphs.

Thm. Any undirected unweighted graph has a $2$-additive spanner with $O(n^{3/2})$ edges.

Pf. The construction of the spanner $S$:

S=Ø
Randomly select n^{1/2} vertices, call the set W
S includes the shortest path trees from all vertices in W 
for all vertices u:  
	if there is an edge (u, w) s.t. w ∈ W:
		add (u, w) in S
	else:
		include all edges (u, v) in S

For a vertex $u$, if the degree of $u$ is $\Omega(n^{1/2})$, w.h.p. it is adjacent to a vertex in $W$. So $|S|=O(n^{3/2})$.

Consider the shortest path from $u$ to $v$ in $G$:

If $u$ or $v$ is in $W$, the shortest path must also be in $S$, it is trivial
Otherwise if the first edge $(u, u') \in S$, recursively consider the $(u', v)$
Otherwise if the first edge $(u, u') \notin S$, $u$ is adjacent to a $w \in W$. We can see that $(u, w)$ and a shortest path from $w$ to $v$ is in $S$. And it's not much longer than the shortest path from $u$ to $v$:

\[d(w, v) \leq d(u, v) + d(w, u) = d(u, v) + 1 \]
so

\[d_S(u, v) \leq d(u, w) + d(w, v) = d(w, v) + 1 \leq d(u, v) + 2. \]

Thm. Any undirected unweighted graph has a $4$-additive spanner with $\tilde{O}(n^{7/5})$ edges.

Pf. $N(w)$: neighbors of $w$. Heavy vertices: vertices with degree $>n^{2/5}$.

Randomly select n^{2/5}*log n vertices, call the set X;
Randomly select n^{3/5}*log n vertices, call the set Y;
S includes the shortest path trees from all vertices in X
for all vertices u:
    if there is an edge (u,w) s.t. w ∈ Y,
        add (u,w) in S
    else
        include all edges (u,v) in S
for every pair of v1, v2 ∈ Y
    for all shortest paths from u1 ∈ N(v1) to u2 ∈ N(v2) with < n^{1/5} heavy vertices
        add the shortest one to S, as well as edges (u1, v1) and (u2, v2)
Heavy u is adjacent to a w ∈ Y
S includes all edges associated with u

Thm [Baswana, Kavitha, Mehlhorn, and Pettie, 2005]. Any undirected unweighted graph has a $6$-additive spanner with $O(n^{4/3})$ edges.

Thm. There is no constant additive spanner with $O(n^{4/3-\varepsilon})$ edges.

Primality test

Checking whether an integer $N$ is a prime number. Expected a algorithm polynomial of the length of the number.

Thm (Fermat’s little theorem). Let $\mathbb{Z}_p=\{0,1,...,p-1\}$ and $\mathbb{Z}_p^+=\{1,...,p-1\}$ for any $p$. If $p$ is a prime,

\[\forall a\in\mathbb{Z}_p^+,a^{p-1}\equiv 1\pmod p. \]

Rem. In fact, $\mathbb{Z}^+_p$ is a group under multiplication module $p$, so the order of any element is a factor of the order of the group.

Rem. Intuitively, we want to use Fermat’s little theorem to test primality, that is, randomly select $a\in\mathbb{Z}^+_p$, and check whether $a^{p-1}\equiv 1\pmod p$. Unfortunately, the converse of Fermat’s little theorem is not always true!

Def. A Carmichael number is a composite number $n$ which satisfies that $\forall a\in \mathbb{Z}_n^+$ that are relatively prime to $n$, $a^{n-1}\equiv 1\pmod n$.

Thm. Let $C(X)$ denotes the number of Carmichael numbers $\le X$, $C(X)>X^{0.333367}$.

Thm. Let $p$ is an odd prime, for an even number $k$ and any $a \in Z_p^+$, if $a^k \equiv 1 \pmod{p}$, then $a^{k/2} \equiv \pm 1 \pmod{p}$.

Pf. Let $b = a^{k/2} \bmod p$. Since $b^2 = c \cdot p + 1$ for an integer $c$, $(b+1)(b-1) = c \cdot p$, so $b$ can only be $1$ or $p-1$.

Alg.

Randomly select a ∈ Z_N^+
Compute a^{N-1} mod N, if not 1, reject  
Let k = N - 1
while (k is even) do 
    k = k/2  
    if (a^k mod N = -1), accept  
    if (a^k mod N ≠ 1 or -1), reject  
accept

Thm. The above algorithm can test primality with high probability.

Pf. First, let's show if $N$ is an odd composite, there must be an $a \in \mathbb{Z}_N^+$ which is relatively prime to $N$ s.t. the algorithm rejects.

If $N = p^i$, consider $t = 1 + p^{i-1}$, then $t^N \equiv 1 \pmod{N}$, so $t^{N-1} \neq 1 \pmod{N}$,
Otherwise, $N = q \cdot r$, find an $h^k \equiv -1 \pmod{N}$ with largest $k = (N-1)/2^i$. By the Chinese remainder theorem, there exists a $t$ such that:

\[\begin{aligned} &t \equiv h \pmod{q} \\ &t \equiv 1 \pmod{r} \end{aligned} \]

therefore,

\[\begin{aligned} &t^k \equiv -1 \pmod{q} \\ &t^k \equiv 1 \pmod{r} \end{aligned} \]

so $t^{2k} \equiv 1 \pmod{N}$ but $t^k \not\equiv \pm 1 \pmod{N}$.

Furthermore, we can show that at least one half of elements $\mathbb{Z}_N^+$ can make the algorithm reject.

For $t \in \mathbb{Z}_N^+$ that are not relatively prime to $N$, of course reject, so we only consider numbers that are relatively prime to $N$.

For such a $t \in Z_N^+$ we get above, if we have two $a, b \in \mathbb{Z}_N^+$ which make the algorithm accept so $a^k \equiv \pm 1 \pmod{N}$, $a^{2k} \equiv 1 \pmod{N}$, and the same as $b$. Then $a \cdot t$ and $b \cdot t$ are distinct elements that makes the algorithm reject since $(a \cdot t)^k \not\equiv \pm 1 \pmod{N}$, $(a \cdot t)^{2k} \equiv 1 \pmod{N}$, the same as $b \cdot t$. If $a \cdot t \equiv b \cdot t \pmod{N}$, $(a-b) t = c \cdot N$ for some integer $c$, which is impossible.

Thus, #accept elements $\leq$ #reject elements.

Randomized Complexity Classes

Def (Bounded-error Probabilistic Poly-time, BPP). $L \in \mathsf{BPP}$ if there is a probabilistic polynomial time (p.p.t.) TM $M$:

\[x \in L \Rightarrow \text{Pr}_y[M(x, y) \text{ accepts}] \geq 2/3,\\ x \notin L \Rightarrow \text{Pr}_y[M(x, y) \text{ rejects}] \geq 2/3. \]

Rem. Why $\frac{2}{3}$? In fact can be any constant between $(\frac{1}{2},1]$. (as long as it is independent of the input)

Given $L$, and p.p.t. TM $M$:

$x \in L \Rightarrow \text{Pr}_y[M(x, y) \text{ accepts}] \geq 1/2+\varepsilon$
$x \notin L \Rightarrow \text{Pr}_y[M(x, y) \text{ rejects}] \geq 1/2+\varepsilon$

We can construct a new p.p.t. TM $M'$ by simulate $M$ for $m=\frac{k}{\varepsilon^2}$ times, each time with independent coin flips and accept if majority of simulations accept. Let $X$ be the random variables that denote the number of wrong outcomes, and $p\le \frac{1}{2}-\varepsilon$ is the probability of wrong outcome each time, then

\[\text{Pr}\left[X\le \frac{m}{2}\right]\le 2^mp^{m/2}(1-p)^{m/2}\le (1-4\varepsilon^2)^{m/2}\approx e^{-2k}. \]

Polynomial Identity Testing

Given a polynomial $p(x_1, x_2, \ldots, x_n)$ as arithmetic formula (fan-out 1):

Multiplication (fan-in 2)
Addition (fan-in 2)
Negation (fan-in 1)

Determine that whether $p$ is identically zero, i.e., is $p(x) = 0$ for all $x \in \mathbb{R}^n$.

It equivalent to "polynomial identity testing" because given two polynomials $p, q$, we can check the identity $p \equiv q$ by checking if $p - q \equiv 0$.

Lem (Schwartz-Zippel). Let

\[p(x_1, x_2, \ldots, x_n) \]

be a total degree $d$ non-zero polynomial, and let $S$ be any subset of integers. Then,

\[\operatorname{Pr}_{r_1, r_2, \ldots, r_n \in S}[p(r_1, r_2, \ldots, r_n) = 0] \leq d/|S| \]

Pf. Induction on number of variables $n$.

Base case: $n = 1$, $p$ is univariate polynomial of degree at most $d$. By the fundamental theorem of algebra, it has at most $d$ roots, so

\[\operatorname{Pr}[p(r_1) = 0] \leq d/|S| \]

Write $p(x_1, x_2, \ldots, x_n)$ as

\[p(x_1, x_2, \ldots, x_n) = \sum_{i\le k} (x_1)^i p_i(x_2, \ldots, x_n) \]

where $k = \max. i$ for which $p_i(x_2, \ldots, x_n)$ not identically zero. By induction hypothesis:

\[\operatorname{Pr}[p_k(r_2, \ldots, r_n) = 0] \leq (d - k)/|S| \]

Whenever $p_k(r_2, \ldots, r_n) \neq 0$, $p(x_1, r_2, \ldots, r_n)$ is a univariate polynomial of degree $k$, so

\[\operatorname{Pr}[p(r_1, r_2, \ldots, r_n) = 0 \mid p_k(r_2, \ldots, r_n) \neq 0] \leq k/|S| \]

Conclude:

\[\operatorname{Pr}[p(r_1, \ldots, r_n) = 0] \leq (d - k)/|S| + k/|S| = d/|S| \]

Alg. For field $\mathbb{F}$, pick a subset $S\subset \mathbb{F}$ of size $3d$. Pick $r_1,r_2,...,r_n$ from $S$ uniformly at random. If $p(r_1,r_2,...,r_n)=0$, answer "yes"; otherwise, answer "no".
Rem. If $p$ identically zero, never wrong. If not, Schwartz-Zippel ensures probability of error at most $1/3$.

Perfect Matching

Prob. Given a bipartite graph $G$, determine whether there is a perfect matching in $G$.

Alg. A perfect matching in a bipartite graph with $n$ vertices each side can also be seen as a permutation of $\{1, \ldots, n\}$. Construct an $n \times n$ matrix $X$: $x_{ij} = 0$ if there is no edge from $A_i$ to $B_i$.

By determinant of adjacency matrix

\[\det(X) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^n x_{i, \sigma_i}, \]

a perfect matching corresponds to a non-zero term in the determinant of $X$. So $\operatorname{det}(X) \equiv 0$ iff there is no perfect matching.

The determinant is a polynomial of degree $n$. As in the polynomial identity testing, we can randomly pick each nonzero $x_{ij}$ from $\{1, \ldots, 3n\}$, and compute $\det(X)$. Computing $\det(X)$ takes $O(n^\omega)$ time, the same as matrix multiplication.

Rem. Determinant of $A$:

\[\operatorname{det}(A) = \sum_{\sigma \in S_n} \text{sgn}(\sigma) \prod_{i=1}^n a_{i, \sigma_i} \]

Permanent of $A$:

\[\operatorname{perm}(A) = \sum_{\sigma \in S_n} \prod_{i=1}^n a_{i, \sigma_i} \]

Then $\operatorname{perm}(A)$ is just the number of perfect matchings in $G$. Determinant is in $\mathsf{P}$, but permanent is $\#\mathsf{P}$-complete, thus $\mathsf{NP}$-hard. i.e., Perfect matching is in $\mathsf{P}$, but number of perfect matching is $\#\mathsf{P}$-complete.

Def (Randomized Poly-time, RP). $L \in \mathsf{RP}$ if there is a p.p.t. TM $M$:

\[x \in L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ accepts}]\ge\frac{1}{2},\\ x \notin L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ rejects}] = 1. \]

Def. (complement of Random Poly-time, coRP). $L \in \mathsf{coRP}$ if there is a p.p.t. TM $M$:

\[x \in L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ accepts}] = 1,\\ x \notin L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ rejects}]\ge\frac{1}{2}. \]

Def. (Zero-error Probabilistic Poly-time, ZPP). $L \in \mathsf{ZPP}$ if there is a p.p.t. TM $M$:

\[x \in L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ accepts}] = 1,\\ x \notin L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ rejects}]=1. \]

Thm. $\mathsf{RP \cap coRP=ZPP}$.

Pf. $\Rightarrow$: $\mathsf{RP \cap coRP\subseteq ZPP}$.

Let $L$ be a language recognized by $\mathsf{RP}$ algorithm $A$ and $\mathsf{coRP}$ algorithm $B$.

Run w on A and B simultaneously  
if A accepts, the answer must be YES  
else if B rejects, the answer must be NO  
else, repeat

In each iteration the probability of halting is $\geq 50\%$. So the chance of having the $k$-th repetition shrinks exponentially. Therefore, the expected running time is polynomial.

$\Leftarrow$: $\mathsf{ZPP\subseteq RP \cap coRP}$

Let $C$ be an algorithm in $\mathsf{ZPP}$. Construct the $\mathsf{RP}$ algorithm using $C$:

Run $C$ for (at least) double its expected running time
If it gives an answer, that must be the answer
If it doesn't return "no".

The $\mathsf{coRP}$ algorithm can be constructed similarly. Therefore, we can conclude that $\mathsf{ZPP}$ $\subseteq$ $\mathsf{RP}\cap\mathsf{coRP}$.

Thm. $\mathsf{RP\subseteq NP}$.

Pf. Let $L\in \mathsf{RP}$. Then there is p.p.t. $M$ s.t.

\[x \in L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ accepts}]\ge\frac{1}{2},\\ x \notin L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ rejects}] = 1. \]

So $x\in L\Leftrightarrow$ $\exists y[M(x,y)\text{ accepts}].$

Open Problem. $\mathsf{NP}\text{ v.s. }\mathsf{BPP}$, $\mathsf{P}\text{ v.s. }\mathsf{BPP}$.

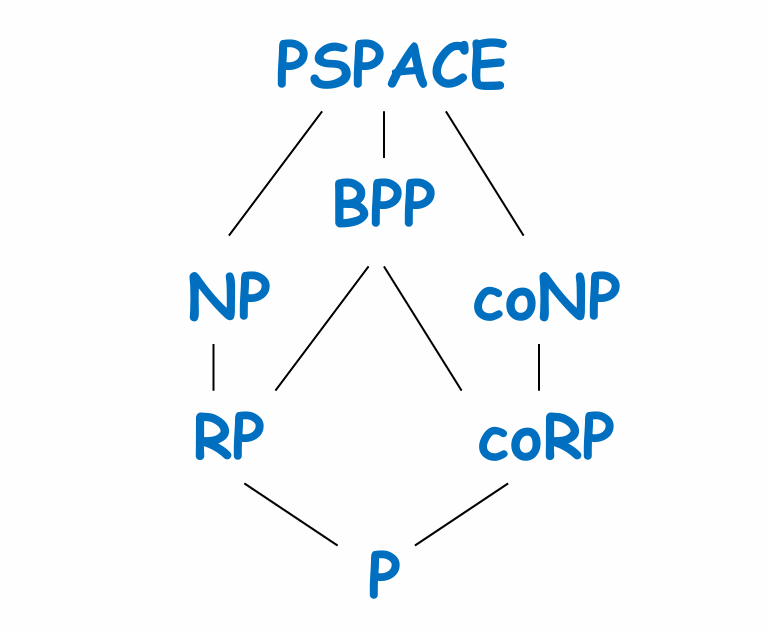
Rem. We even don’t know whether $\mathsf{BPP}$ different from $\mathsf{EXP}$.

Thm (Sipser–Gács–Lautemann theorem). $\mathsf{BPP\subseteq (\Sigma_2^p\cap\Pi_2^p)}$.

Pf. By error reduction, for any $\mathsf{BPP}$ language $L$, there is a p.p.t. $M$ s.t.

\[x \in L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ accepts}] \geq 1-\frac{1}{2 m}\\ x \notin L \Rightarrow \operatorname{Pr}_y[M(x, y) \text{ accepts}] \leq \frac{1}{2 m} \]

assuming $|y|=m$. Then we claim that

\[x \in L \Rightarrow \left(\exists y_1, \ldots, y_m\right)(\forall z)[\text{one of } M(x, y_i \oplus z) \text{ accepts}],\\ x \notin L \Rightarrow \left(\forall y_1, \ldots, y_m\right)(\exists z)[\text{none of } M(x, y_i \oplus z) \text{ accepts}] \]

If $x \notin L$, only $\leq \frac{1}{2 m} 2^m$ of random strings $y$ can make $M(x, y)$ accept.

\[\text{Pr}_{y_i}[M(x, y_i \oplus z) \text{ accept}] \leq \frac{1}{2 m} \]
By union bound,

\[\operatorname{Pr}_{y_1, y_2, \ldots, y_m}[\text{all of } M(x, y_i \oplus z) \text{ rejects}] \leq \frac{1}{2}. \]
So for any $y_1, \ldots, y_m$, there exists $z$ such that all of $M(x, y_i \oplus z)$ reject.
If $x\in L$, for any $z$:

\[\text{Pr}_{y_i}[M(x, y_i \oplus z) \text{ rejects}] \leq \frac{1}{2 m} \]
So

\[\operatorname{Pr}_{y_1, y_2, \ldots, y_m}[\text{all of } M(x, y_i \oplus z) \text{ rejects}] \leq \left(\frac{1}{2 m}\right)^m \]
Since $2^m\left(\frac{1}{2 m}\right)^m<1$, there exists $y_1, \ldots, y_m$, there for all $z$ such that all of $M(x, y_i \oplus z)$ accept.

So far $\mathsf{BPP\subseteq \Sigma^p_2}$. Since $\mathsf{BPP}$ is closed under complement, $\mathsf{BPP} \subseteq \Pi_2$.

Prop. If $\mathsf{P=NP}$, $\mathsf{PH}$ collapses to $\mathsf{P}$, then $\mathsf{P=BPP}$.

Ex. Two important problems by randomized algorithms are shown to have deterministic algorithms:

Primality:
- $\mathsf{BPP}$: Solovay-Strassen primality test [1977]
- $\mathsf{P}$: AKS primality test [2002]
UPATH (undirected connectivity):
- $\mathsf{RL}$: by random walks [1979]
- $\mathsf{L}$: by expander, Reingold [2005]

Matrix Multiplication

The $\mathrm{O}\left(n^{2.81}\right)$ bound of Strassen was improved by Coppersmith and Winograd to $\mathrm{O}\left(n^{2.376}\right)$. The current bound is $\mathrm{O}\left(n^{2.371339}\right)$ [Alman, Duan, V.Williams, Xu, Xu, Zhou].

We let $2 \leq \omega < 2.371339$ be the exponent. Many believe that $\omega=2+o(1)$.

Prob (Witness for 0-1 Matrix Multiplication). Given Boolean matrix $A,B$, and $C=AB$, compute a matrix $W$ such that:

if $C_{ij}>0$, $W_{ij}$ is one of the $k$ such that $A_{i,k}=B_{k,j}=1$.

You are given the oracle to compute matrix multiplication.

Lem. Suppose there are $n$ boxes, $k$ of which contain balls. We can choose some boxes and open them simultaneously, with a constant probability that exactly once there is a ball in the box.

Pf. If we i.i.d. randomly open a box, for $d$ times, the probability that exactly once there is a ball in the box is:

\[d\cdot\frac{k}{n}\cdot\left(1-\frac{k}{n}\right)^{d-1} \]

When $d=\frac{n}{k}$, it is $>\frac{1}{e}$.

Rem. When $\frac{n}{2k}\le d\le \frac{n}{k}$, the probability is $>\frac{1}{2e}$.

Alg. (For witness for 0-1 Matrix Multiplication). Enumerate $t=1,2,4,8,...$, randomly choose a subset $S\subseteq [n]$ of size $t$, and make $A'_{ij}=j$ iff $A_{ij}=1$ and $j\subseteq S$, otherwise $A'_{ij}=0$. Calculate $A'\cdot B$ and check whether the result gives the real witness for each position. For each $t$, we repeat the sampling for $O(\log n)$ times.

Prob. In a undirected graph $G$, check whether $G$ contains a triangle.

Alg. Trivial algorithm: checking every triple of vertices $(u,v,w)$. Time: $O(n^3)$.

Alg. Let $A_{ij}=1$ iff $(i,j)\in E$. Consider $A^2$: $(A^2)_{ij}=\sum_kA_{ik}A_{kj}>0$ iff $\exists k$ s.t. $A_{ik}=A_{kj}=1$. So $G$ has a triangle iff $\exists (i,j)$ s.t. $A_{ij}=1$ and $(A^2)_{ij}=1$.

Rem. Checking whether a graph contains a $4$-cycle: There must be $(i,j)$ such that $(A^2)_{ij}\ge 2$.

What about the $4$-node subgraph is exactly a $4$-cycle?

Thm (Vassilevska, Wang, Williams, Yu 2014). All types of $4$-node subgraphs except “clique” and “independent set” can be found in $\tilde{O}(n^w)$ time with high probability.

Pf. A diamond is the complement of an edge and two independent vertices. Consider

\[X=\sum_{(u,v)\in E}\binom{(A^2)_{u,v}}{2}. \]

"Diamond" is counted $1$ times for $X$, and "clique" is counted $6$ times for $X$.

If $X\bmod 6\neq 0$, then of course the graph contains a diamond.
Otherwise, we randomly delete some vertices. With some probability, the number of diamonds will not be a multiple of 6, then return true. We can run this procedure many times, if the graph contains no diamond, it always return false.

For $4$-cycle, consider

\[Y=\sum_{(u,v)\notin E}\binom{(A^2)_{u,v}}{2}. \]

"$4$-cycle" is counted $2$ times for $Y$, and "diamond" is counted $1$ times for $Y$.

So $X-Y=6(\#\text{clique})-2(\#\text{4-cycle})$, using similar idea we can check whether a graph contains a $4$-cycle.

Interactive Proof

Proof Systems

Given language $L$, goal is to prove $x \in L$.

Def (Classical Proof System). A classical proof system for $L$ is a verification algorithm $V$ satisfying

completeness: $x \in L \Rightarrow \exists \text{ proof}$, $V$ accepts $(x,\text{proof})$
"true assertions have proofs"
soundness: $x \notin L \Rightarrow \forall\text{ proof*}$, $V$ rejects $(x,\text{proof}^*)$
"false assertions have no proofs"
efficiency: For all $x$ and $\text{proof}$, $V(x)$ runs in polynomial time in $|x|$ (so $|\text{proof}|$ is poly in $|x|$)

Ex. $L \in \mathsf{NP}$ iff expressible as

\[L=\left\{x \mid \exists y, |y|<|x|^k, (x, y) \in R\right\} \]

and $R \in \mathsf{P}$.

$\mathsf{NP}$ is the set of languages with classical proof systems ($R$ is the verifier).

Def (Deterministic Interactive Proof System). An deterministic interactive proof system for $L$ is an interactive protocol $(P, V)$

completeness: $x \in L \Rightarrow \exists P,(V,P)(x)=1$.
soundness: $x \notin L \Rightarrow\forall P^*,(V,P^* )(x)=0.$

where the protocol is a sequence of interaction:

input: $x$
$a_1=V(x)$
$a_2=P(x,a_1)$
$\cdots$
$a_k=V(x,a_1,...,a_{k-1})$

$(V,P)(x)=a_k$ is the output of the verifier at the end of the interaction.

Rem. Prover $P$ can be a all-powerful machine, while Verifier $V$ must be a polynomial time machine.

Def. $\mathsf{dIP}=\{L:L\text{ has a deterministic interactive proof system}\}$.

Thm. $\mathsf{dIP=NP}$.

Pf. We can see that the transcript $a_1,...,a_{k-1}$ is the certificate for $x\in L$. We just need to check whether $V(x)=a_1, V\left(x, a_1, a_2\right)=a_3, \ldots$, and $V\left(x, a_1, \ldots, a_{k-1}\right)=1$.

We need to introduce randomness into the interactive proof system!

Def (Interactive Proof System). An interactive proof system for $L$ is an interactive protocol $(P,V)$

completeness: $x \in L \Rightarrow \exists P$

\[\text{Pr}_r[V \text{ accepts in } (P,V)(x)] \geq 2/3 \]
soundness: $x \notin L \Rightarrow \forall P^*$

\[\text{Pr}_r[V \text{ accepts in } (P^*, V)(x)] \leq 1/3 \]
efficiency: $V$ is p.p.t. machine based on random variable $r$. ($P$ cannot see $r$).

where the protocol is a sequence of interaction:

input $x$, random variable $r\in\{0,1\}^m$
$a_1=V(x,r)$
$a_2=P(x,a_1)$
$a_3=V(x,r,a_1,a_2)$
$a_4=P(x,a_1,a_2,a_3)$
$\cdots$
$a_k=V(x,r,a_1,...,a_{k-1})$

Def. $\mathsf{IP} = \{L : L \text{ has an interactive proof system}\}.$

Graph Isomorphism

Def. Graphs $G_0=(V, E_0)$ and $G_1=(V, E_1)$ are isomorphic ($G_0 \cong G_1$) if exists a permutation $\pi: V \rightarrow V$ for which

\[(x, y) \in E_0 \Leftrightarrow (\pi(x), \pi(y)) \in E_1 \]

Let $GI={(G_0, G_1): G_0 \cong G_1}$ and $GNI=\overline{GI}$ (complement of $GI$).

Rem. Clearly, $GI\in\mathsf{NP}$. But not known to be in $\mathsf{P}$, or $\mathsf{NP}$-complete. $GNI$ is also not known to be in $\mathsf{NP}$.

Thm (GMW). $GNI \in \mathsf{IP}$.

Pf. Consider the following protocol: Each time the verifier flip a coin $c\in\{0,1\}$ and pick a random $\pi$, send $H=\pi(G_c)$. The prover will determine whether $H\cong G_0$, if so, return $r=0$; otherwise, return $r=1$. Then the verifier accept iff $r=c$.

completeness: if $G_0$ is not isomorphic to $G_1$ then $H$ is isomorphic to exactly one of $(G_0, G_1)$
prover can choose correct $r$.
soundness: if $G_0 \cong G_1$ then prover sees the same distribution on $H$ for $c=0, c=1$, so any prover $P^*$ can succeed with probability at most $1/2$.

Rem. $GNI\in\mathsf{IP}$ suggests $\mathsf{IP}$ (maybe) more powerful than $\mathsf{NP}$, since we don’t know how to show $GNI$ in $\mathsf{NP}$.

Thm (LFKN). $\mathsf{coNP \subseteq IP}$.

Pf. We will prove $\#\text{SAT}=\{(\phi, k): \text{CNF } \phi \text{ has exactly } k \text{ satisfying assignments}\}$ is in $\mathsf{IP}$.

First, transform $\phi(x_1,...,x_n)$ into polynomial $p_\phi(x_1,x_2...,x_n)$ of degree $d$ over a field $GF(q)$ where $q>2^n$ is a prime by recursively:

$x_i \rightarrow x_i$
$\neg \phi \rightarrow (1-p_\phi)$
$\phi \wedge \phi' \rightarrow (p_\phi)(p_{\phi'})$
$\phi \vee \phi' \rightarrow 1-(1-p_\phi)(1-p_{\phi'})$

Notice that for all $x \in \{0,1\}^n$ we have $p_\phi(x)=\phi(x)$ and degree $d \leq |\phi|$.

Lem (fundamental theorem of algebra). Every non-zero, single-variable, degree $d$ polynomial (with complex coefficients) has, counted with multiplicity, exactly $d$ roots.

Now prover wishes to prove:

\[k=\sum_{x_1=\{0,1\}} \sum_{x_2=\{0,1\}} \cdots \sum_{x_n=\{0,1\}} p(x_1, x_2, \ldots, x_n) \]

Consider the following so-called "sumcheck protocol":

If $n=1$, verifier checks whether $p(1)+p(0)=k$
Else, prover sends a one-variable polynomial $s(z)$, which suppose to be

\[k_z=\sum_{x_2=\{0,1\}} \cdots \sum_{x_n=\{0,1\}} p_\phi(z, x_2, \ldots, x_n) \]
Verifier rejects if $s(0)+s(1)\neq k$, otherwise picks a random variable $a\in GF(q)$, recursively check whether

\[s(a)=\sum_{x_2=\{0,1\}} \cdots \sum_{x_n=\{0,1\}} p_\phi(a, x_2, \ldots, x_n) \]

Completeness is obviously.

For soundness, if the prover cheats by sending an $s(z)$ such that $s(0)+s(1)=k$, then $s(z)$ is not identical to $k_z$. So the number of $a$ s.t. $s(a)=k_a$ is the number of roots of $s(z)-k_z$, which is at most the degree $d$. So the probability that $s(a)\neq z_a$ is $\ge 1-d/q$. By union bound, the probability that the inequality always holds for $n$ recursions is:

\[\geq \left(1-\frac{d}{q}\right)^n \geq \left(1-\frac{|\phi|}{2^n}\right)^n\ge 1-\frac{n|\phi|}{2^n} \geq 1-\frac{\text{poly}(n)}{2^n} \gg \frac{2}{3}. \]

So far, $\#\text{SAT}\in\mathsf{IP}$. On the other hand, $\#\text{SAT}$ is $\mathsf{coNP}$-hard. So $\mathsf{coNP\subseteq IP}$.

Rem. We have already seen that $\mathsf{NP,coNP\subseteq IP}$. In fact, it's more powerful:

Thm (Shamir 1990). $\mathsf{IP = PSPACE}$.

Pf. For $\mathsf{IP \subseteq PSPACE}$, simply enumerate all possible interactions, explicitly calculate acceptance probability.

For $\mathsf{PSPACE \subseteq IP}$, consider a protocol for TQBF:

First, do arithmetization. Let $\forall x_1 \exists x_2 \forall x_3 \ldots \exists x_n \phi_0(x_1, x_2, \ldots, x_n)$ be an instance of TQBF. Let

\[\phi=(\forall x_1)(Rx_1)(\exists x_2)(Rx_1)(Rx_2)...(\exists x_n)(Rx_1)(Rx_2)...(Rx_n)\phi_0(x_1,...,x_n). \]

Then recursively transform:

$\left(\exists x_i\right) \phi \rightarrow \sum_{x_i=\{0,1\}} p_\phi$
$\left(\forall x_i\right) \phi \rightarrow \prod_{x_i=\{0,1\}} p_\phi$
$\left(R x_i\right) \phi(x_1, \ldots x_i, \ldots, x_n) \rightarrow x_i \cdot p_\phi(x_1, \ldots x_{i-1}, 1, x_{i+1}, \ldots x_n) + (1-x_i) \cdot p_\phi(x_1, \ldots x_{i-1}, 0, x_{i+1}, \ldots x_n)$

One can verify that $p_\phi$ keeps a multilinear function.

Prover wishes to prove:

\[k=p_\phi. \]

Define: $\phi=(O x_1) \phi'(x_1)$, where $O=\forall, \exists$, or $R$. (when $O=R$, $x_1$ is already assigned $a_1$).

Consider the following so-called "TQBF protocol":

Prover sends a one-variable polynomial $s(x_1)$, which suppose to be $p_{\phi'}(x_1)$
Verifier checks:
- if $O=\forall$, check $s(0)s(1)=k$
- if $O=\exists$, check $s(0)+s(1)=k$
- if $O=R$, check $a_1 s(1)+(1-a_1)s(0)=k$
  
  if it is not equal, rejects; otherwise picks a random variable $a$ in $GF(q)$, recursively check whether $s(a)=p_{\phi'}(a)$.

Similar to the protocol of $\#\text{SAT}$, the probability of soundness is:

\[\geq \left(1-\frac{d}{2^n}\right)^{n^2} \geq 1-\frac{\text{poly}(n)}{2^n}\gg 2/3. \]

Arthur-Merlin Games

$\mathsf{IP}$ permits verifier to keep coin-flips private, is it neccessary?

Def. Arthur-Merlin game: interactive protocol in which coin-flips are public. Arthur (verifier) may as well just send results of coin-flips and ask Merlin (prover) to perform any computation Arthur would have done. Formally, Arthur-Merlin game for $L$ is an interactive protocol $(P,V)$

completeness: $x \in L \Rightarrow \exists P$

\[\text{Pr}_r[V \text{ accepts in } (P,V)(x)]=1. \]
soundness: $x \notin L \Rightarrow \forall P^*$

\[\text{Pr}_r[V \text{ accepts in } (P^*, V)(x)] \leq \frac{1}{2} \]
efficiency: $V$ is p.p.t. machine based on random variable $r$. ($P$ CAN see $r$).

where the protocol is a sequence of interaction (if Arthur goes first for example):

input $x$
Arthur randomly samples variable $r\in\{0,1\}^m$, $a_1=r$
$a_2=P(x,r)$
$a_3=V(x,r,a_2)$
$a_4=P(x,r,a_2,a_3)$
$\cdots$
$a_k=V(x,r,...,a_{k-1})$

Clearly, $\mathsf{Arthur}\text{-}\mathsf{Merlin\subseteq IP}$. Recall in the above proof, TQBF protocol only need public coins. So immediately, $\mathsf{PSPACE}\subseteq\mathsf{Arthur}\text{-}\mathsf{Merlin}$. Combining them gives

Thm. $\mathsf{PSPACE}=\mathsf{IP}=\mathsf{Arthur}\text{-}\mathsf{Merlin}.$

Rem. Public coins are at least as powerful as private coins!

Def. Delimiting # of rounds:

$\mathsf{AM}[k]=$ Arthur-Merlin game with $k$ messages, Arthur (verifier) goes first.

$\mathsf{MA}[k] =$ Arthur-Merlin game with $k$ messages, Merlin (prover) goes first.

Ex. $\mathsf{MA}[2]$: $1$-message protocol where Merlin sends Arthur a message, and then Arthur decides whether to accept or not by running a probabilistic polynomial time computation. (similar to $\mathsf{NP}$, just the verifier can use randomness.)

$L\in \mathsf{MA}[2]$ iff $\exists$ poly-time language $R$ s.t.

\[x\in L\Rightarrow(\exists m)\text{Pr}_r[(x,m,r)\in R]=1\\ x\notin L\Rightarrow(\forall m)\text{Pr}_r[(x,m,r)\in R]\le\frac{1}{2} \]

$\mathsf{AM}[2]$: Arthur tosses some random coins and sends the outcome of all his coin tosses to Merlin, Merlin responds with a purported proof, and Arthur deterministically verifies the proof.

$L\in\mathsf{AM}[2]$ iff $\exists$ poly-time language $R$ s.t.

\[x\in L\Rightarrow\text{Pr}_r[(\exists m)(x,m,r)\in R]=1\\ x\notin L\Rightarrow\text{Pr}_r[(\exists m)(x,m,r)\in R]\le\frac{1}{2} \]

Thm. $\mathsf{MA}[2]\subseteq\mathsf{AM}[2]$.

Pf. Given $L\in\mathsf{MA}[2]$,

\[x\in L\Rightarrow(\exists m)\text{Pr}_r[(x,m,r)\in R]=1\Rightarrow\text{Pr}_r[(\exists m)(x,m,r)\in R]=1,\\ x\notin L\Rightarrow(\forall m)\text{Pr}_r[(x,m,r)\in R]\le\varepsilon\Rightarrow \text{Pr}_r[(\exists m)(x,m,r)\in R]\le 2^{|m|}\varepsilon. \]

By sending $t$ times the independent random strings $r$, we can make error exponentially small: $2^{|m|}\varepsilon=2^{|m|}2^{-t}\le\frac{1}{2}$.

Thm. For any constant $k\ge 2$, $\mathsf{AM}[k]=\mathsf{AM}[2]$.

Pf. We have shown that $\mathsf{MA}[2]\subseteq\mathsf{AM}[2]$. So we can move all of Arthur’s messages to beginning of interaction.

We use $\mathsf{MA}$ and $\mathsf{AM}$ to denote $\mathsf{MA}[2]$ and $\mathsf{AM}[2]$ respectively.

Thm. $\mathsf{AM}\subseteq \Pi_2$.

Pf. $L\in\Pi_2$ iff $\exists R\in \mathsf{P}$ s.t.

\[x\in L\Rightarrow \text{Pr}_r[(\exists m)(x,m,r)\in R]=1\\ x\notin L\Rightarrow \text{Pr}_r[(\exists m)(x,m,r)\in R]<1. \]

Thm. $\mathsf{NP\subseteq MA}$.

Pf. We can show that $L\in \mathsf{MA}$ iff $\exists R\in \mathsf{P}$ s.t.

\[x\in L\Rightarrow (\exists m)\text{Pr}_r[(x,m,r)\in R]\ge \frac{2}{3}\\ x\notin L\Rightarrow (\forall m)\text{Pr}_r[(x,m,r)\in R]\le \frac{1}{3}. \]

by similar proof to $\mathsf{BPP\subseteq \Pi_2}$.

On the other hand, $L\in \mathsf{NP}$ iff $\exists R\in \mathsf{P}$ s.t.

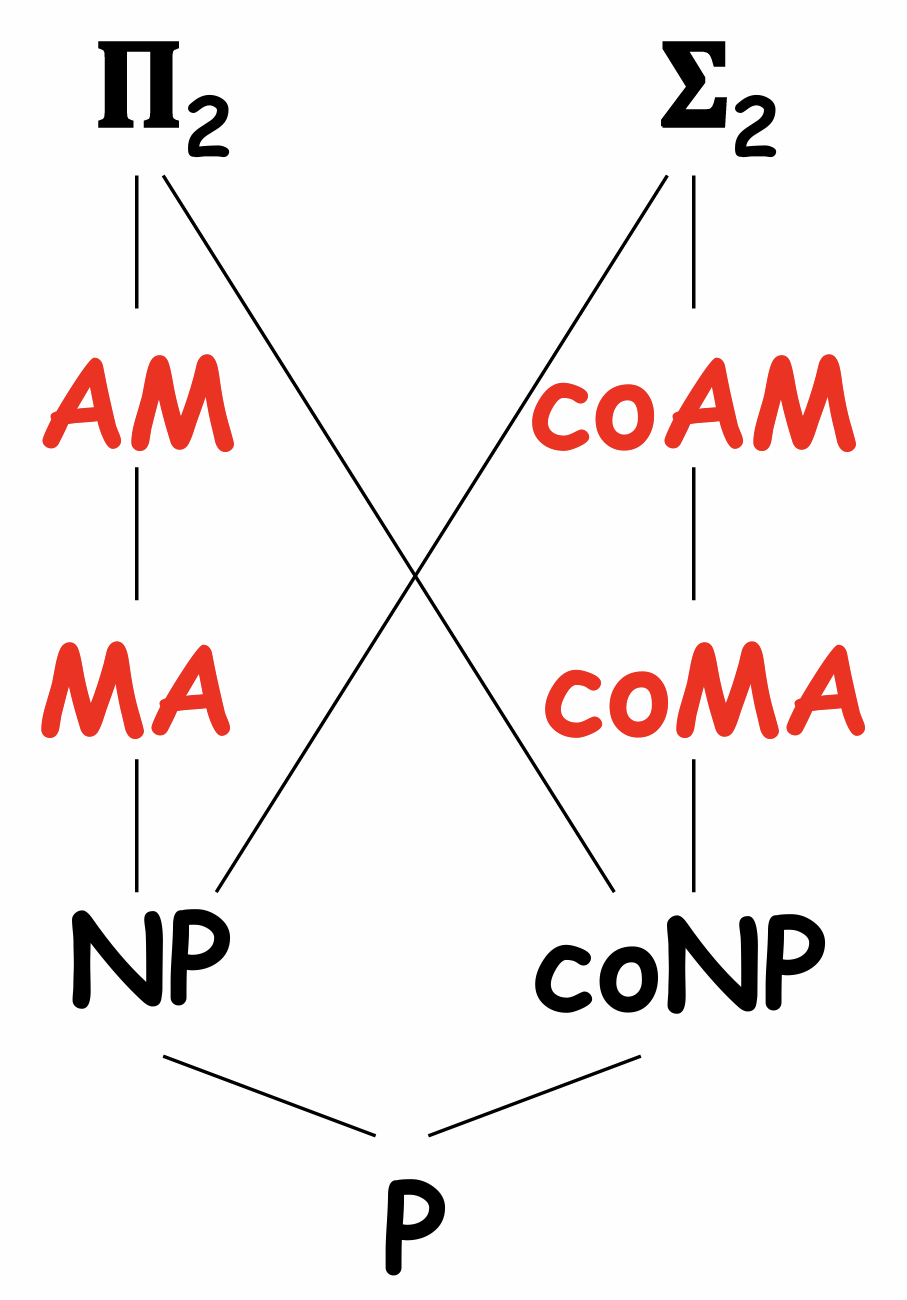
\[x\in L\Rightarrow (\exists m)\text{Pr}_r[(x,m,r)\in R]\ge \frac{2}{3}\\ x\notin L\Rightarrow (\forall m)\text{Pr}_r[(x,m,r)\in R]=0. \]

Def (Pairwise independent hash functions). A pairwise independent hash functions is a family $H$ of functions $\{0,1\}^m \rightarrow \{0,1\}^k$, satisfying

for all $x,y$,

\[\text{Pr}_{h\in H}[h(x)=y]=2^{-k}. \]
pairwise independent: for all $x, x' \in \{0,1\}^m$ with $x \neq x'$, for all $y, y' \in \{0,1\}^k$,

\[\text{Pr}_{h \in H}[h(x)=y \text{ and } h(x')=y']=2^{-2k}. \]

Rem. In finite field $GF(2^m)$, an example of $H(x)$ is $ax+b$ for $a, b \in GF(2^m)$, and we can truncate the last $m-k$ bits to make it $k$ bits.

Ex. $\text{GNI}\in\mathsf{AM}$.

Pf. Define

\[S=\{(H, \pi) ; H \cong G_0 \text{ or } H \cong G_1 \text{ and } \pi \in \text{aut}(H)\}, \]

where $\text{aut}(H)$ is the set of permutation $\pi$ such that $\pi(H)=H$. So if $G_0 \cong G_1, |S|=n!$, otherwise $|S|=2n!$.

If we need to check $|S|\ge 2^k$ or $|S|\le 2^{k-1}$, Goldwasser-Sipser set lower bound protocol works:

Verifier: randomly pick a pairwise independent hash function $h: \{0,1\}^m \rightarrow \{0,1\}^{k+1}$, and randomly pick $y\in \{0,1\}^{k+1}$.
Prover: send $x \in S$ such that $h(x)=y$, and a certificate that $x \in S$.
Verifier: accept iff $h(x)=y$ and $x \in S$.

We consider $\text{Pr}_{h, y}[\exists x \in S: h(x)=y]$. For all $y$,

\[\text{Pr}_{h,y}[\exists x \in S: h(x)=y] \leq \sum_{x \in S} \text{Pr}_{h,y}[h(x)=y]=\frac{|S|}{2^{k+1}} ,\\ \text{Pr}_{h,y}[\exists x \in S: h(x)=y] \geq \sum_{x \in S} \text{Pr}_{h,y}[h(x)=y]-\frac{1}{2}\sum_{x \neq x' \in S} \text{Pr}_{h,y}[h(x)=h(x')=y] \geq \frac{|S|}{2^{k+1}}-\frac{1}{2}\frac{|S|^2}{2^{2k+2}}. \]

So when $|S|\ge2^{k}$, $\text{Pr}[V \text{ accepts}] \geq \frac{3}{8}$; when $|S|\le 2^{k-1}$, $\text{Pr}[V \text{ accepts}] \leq \frac{1}{4}$.

We can use it to determine whether $|S|=n!$ or $|S|=2n!$.

Thm. If $\mathsf{coNP\subseteq AM}$, then $\mathsf{PH=AM}$.

Pf. Suffices to show $\Sigma_2 \subseteq \mathrm{AM}$ (and use $\mathrm{AM} \subseteq \Pi_2$). $L \in \Sigma_2$ iff $\exists R\in \mathsf{P}$

\[\begin{aligned} & x \in L \Rightarrow (\exists y )(\forall z) (x, y, z) \in R \\ & x \notin L \Rightarrow (\forall y)( \exists z) (x, y, z) \notin R \end{aligned} \]

Merlin sends $y$, then $\mathsf{AM}$ exchange decides $\mathsf{coNP}$ query: $\forall z (x, y, z) \in R$ ?

Cor. If GI is $\mathsf{NP}$-complete then $\mathsf{PH=AM}$.

Pf. GI $\mathsf{NP}$-complete $\Rightarrow$ GNI $\mathsf{coNP}$-complete $\Rightarrow$ $\mathsf{coNP} \subseteq \mathsf{AM} \Rightarrow \mathsf{PH =AM}$.

Multiprover Interactive Proofs

What about there are two or more provers?

Important: provers are not allowed to communicate with each other! Otherwise it's the same as only one prover!

Def. A $k$-prover interactive proof system for $L$ is an interactive protocol $(P_1,...,P_k,V)$

completeness: $x \in L \Rightarrow \exists P_1,...,P_k$

\[\text{Pr}_r[V \text{ accepts in } (P_1,...,P_k,V)(x)] \geq 2/3 \]
soundness: $x \notin L \Rightarrow \forall P_1^*,...,P_k^*$

\[\text{Pr}_r[V \text{ accepts in } (P_1^*,...,P_k^*, V)(x)] \leq 1/3 \]
efficiency: $V$ is p.p.t. machine based on random variable $r$. ($P_1,...,P_k$ cannot see $r$).

where the protocol is a sequence of interaction:

input $x$, random variable $r\in\{0,1\}^m$
$a_{1,1}=V(x,r,1)$
$a_{1,2}=V(x,r,2)$
$\cdots$
$a_{1,k}=V(x,r,k)$
$a_{2,1}=P_1(x,a_{1,1})$
$a_{2,2}=P_2(x,a_{1,2})$
$\cdots$
$a_{2,k}=P_k(x,a_{1,k})$
$a_{3,1}=V(x,r,a_{1,1},...,a_{1,k},a_{2,1},...,a_{2,k},1)$
$\cdots$
$a_{3,k}=V(x,r,a_{1,1},...,a_{1,k},a_{2,1},...,a_{2,k},k)$
$a_{4,k}=P_1(x,a_{1,1},a_{2,1})$
$\cdots$

Def. $L\in k\text{-}\mathsf{MIP}$ iff $\{L:L\text{ has a }k\text{-prover interactive proof system}\}$.

Let $M^O$ be a probabilistic polynomial time TM with access to an oracle $O$.

Def. Let $L$ be a language. We say $L\in\mathsf{POM}$ iff:

\[\begin{aligned} & x \in L \Rightarrow (\exists O) \text{Pr}[M^O \text{ accepts } x] \geq 2 / 3 \\ & x \notin L \Rightarrow (\forall O) \text{Pr}[M^O \text{ accepts } x] \leq 1 / 3 \end{aligned} \]

Thm. $2\text{-}\mathsf{MIP}=\mathsf{poly}\text{-}\mathsf{MIP}=\mathsf{POM}$.

Pf. $\mathsf{poly}\text{-}\mathsf{MIP}\subseteq\mathsf{POM}$: Let oracle $O$ answer query $P_i(x,a_{1,i}, \ldots,a_{j,i})$.

$\mathsf{POM\subseteq 2}\text{-}\mathsf{MIP}$: Whenever the oracle machine asks the oracle, it instead asks Prover 1. To check whether Prover 1 cheated, randomly choose a step and check with the other prover.

Thm (Babai, Fortnow, Lund 1991). $\mathsf{MIP=NEXP}$.

Decision Trees

Def. Let $f:\{0,1\}^n\to\{0,1\}$ be some function. A decision tree of $f$ is a binary tree $t$ that each node is labeled a variable $i$. For any input $x$:

begin at the root.
let $i$ be the label on the current node. If $x_i=0$, go left; if $x_i=1$, go right.
the output at the leaf is $f(x)$.

Def. For a tree $t$ and input $x$, $\operatorname{cost}(t, x)$ is the number of bits of $x$ examined by $t$. The decision tree complexity of a function $f$:

\[D(f)=\min_{t \in \text{T}_f} \max_{x \in \{0,1\}^n} \text{cost}(t, x). \]

where $\mathrm{T}_f$ is the set of decision trees that compute $f$.

Ex. OR function:

\[f(x_1, x_2, \ldots, x_n) = x_1 \vee x_2 \vee \ldots \vee x_n \]

Lower bound of decision trees: No smaller depth than the trivial bound of $n$.

Address function: $(n=k+2^k)$

\[f(x_1, \ldots, x_k,y_1,\ldots y_{2^k}) = y_x \]

We can show that $k<D(f)\le k+1<\log n+1$.

"Non-deterministic" version of decision tree complexity:

Def. A "$0$-certificate" for $x$ of a function $f:\{0,1\}^n \rightarrow \{0,1\}$ is a subset $S \subseteq \{1,2,\ldots,n\}$ s.t. $f(x')=0$ for all $x'|_S = x|_S$

where $x|_S$denotes the substring of $x$ in the coordinates in $S$.

“$1$-certificate” is similar such that $f(x’)=1$ for all $x'|_S = x|_S$.

Def. Certificate complexity $C(f)$ for a function $f$ is the minimum $k$ s.t. every $x$ has an $f(x)$-certificate of size $\leq k$.

Ex. graph connectivity

Graph connectivity function $f$:

Input: an undirected graph $G$ with $n$ vertices, represented by a string of length $\binom{n}{2}$ (adjacency matrix)
Output: whether the graph is connected

Then

$D(f)=\binom{n}{2}$.
$C(f)=\max\{n^2/4,n-1\}=n^2/4$.
- 1-certificate: a spanning tree
- 0-certificate: a "no-edge" cut

Thm. $C(f)\le D(f)$.

Thm. $D(f)\le C(f)^2$.

Pf. Construct the decision tree for $f$

DT(f):
	if f is a constant, return the answer
	Find a 0-certificate S for some f(x)=0
	Construct the decision tree for all bits in S
	For every y∈{0,1}^{|S|}
		call DT(f|_{S=y})

Notice that Every $0$-certificate must intersect every $1$-certificate, otherwise they will be contradicting to each other.

So every $1$-certificate will shrink by $1$ after each call. Thus, in total we need $C(f)$ recursive calls, and the depth of the decision tree is at most $C(f)^2$.

Circuit Complexity

Circuit Families

Def (Boolean Circuit). A Boolean circuit $C$ is a finite directed acyclic graph with a Boolean operator or a variable on each node. Its size is the number of gates and depth is the length of the longest path from input to output.

Rem. $C$ computes function $f:\{0,1\}^n\to\{0,1\}$ in nature way. Every such function can be computed by a circuit of size at most $O(n2^n)$.

Def. A circuit family $\{C_n\}$ has circuit for all input length. We say that $\{C_n\}$ computes $f$ if and only if for all $x$, $C_{|x|}(x)=f(x)$.

Def. $T(n)$-size circuit family is a sequence $\{C_n\}$ of Boolean circuits where the size of $C_n$ is not greater than $T(n)$ for every $n$.

\[\mathsf{SIZE}(T(n))=\{\text{languages decided by }T(n)\text{-size circuit families}\{C_n\}\}. \]

Specifically,

\[\mathsf{P/poly}=\bigcup_c\mathsf{SIZE}(n^c)=\{\text{languages decided by polynomial-size circuit families}\}. \]

Thm. Suppose a TM $M$ running in time $t(n)$ decides language $L$, we can build circuit family $\{C_n\}$ of size $|C_n|=O(t(n)^2)$ that decides $L$.

Pf. Consider the $t(n)\times t(n)$ table of computation history. $\Gamma$ is the set of tape symbols, $Q$ is the set of states, so the possible elements of entry $(i, j)$ in the table is in $\Gamma \cup Q$.

We assign each entry $(i, j)$ $|\Gamma \cup Q|$ Boolean variables, so that $v(i, j, a)=1$ iff the entry $(i, j)$ in the table is $a$; otherwise $v(i, j, a)=0$. Then, construct the entire circuit by $v(i, j, a)$ for all $i, j \in [1, t(n)]$ and $a \in \Gamma \cup Q$.

In the circuit, for every variable $v(i, j, d)$:

\[v(i, j, d) = \bigvee_{(a, b, c) \text{ yields } d} (v(i-1, j-1, a) \wedge v(i-1, j, b) \wedge v(i-1, j+1, c)) \]

For the last line, check whether it has the accept state.

So the circuit complexity for a TM in $t(n)$ time is $O(t(n)^2)$.

Cor. $\mathsf{P\subseteq P/poly}$.

Rem. What about the other direction? The answer is, no. In fact, even an undecidable language can be in $\mathsf{P/poly}$, e.g., $\{1^n|n\text{ is the code of a TM with no input which halts}\}$.

This reveals a strange aspect of circuit family: can "encode" (potentially uncomputable) information in family specification.

Def. Circuit family $\{C_n\}$ is logspace uniform iff a TM $M$ outputs $C_n$ on input $1^n$ and runs in $O(\log n)$ space.

Thm. $\mathsf{P} = \{\text{languages decidable by logspace uniform, polynomial-size circuit families } \{C_n\}\}$.

Pf.

($\Rightarrow$) already saw $\mathsf{P \subseteq P/poly}$, you can check it is logspace uniform.

($\Leftarrow$) on input $x$, generate $C_{|x|}$, evaluate it and accept iff output $=1$.

Def. $L\in\mathsf{TIME}(t(n))/f(n)$ iff

There exists $A(n)$ s.t. $|A(n)| \leq f(n)$
There exists a TM $M$ decides $L$ with advice $A(n)$ in time $t(n)$

Ex.

\[\mathsf{P/poly} = \bigcup_k \mathsf{TIME}(n^k)/n^k \]

People may believe $\mathsf{NP}\not\subseteq\mathsf{P/poly}$.

Thm (Karp-Lipton). if SAT has poly-size circuits then $\mathsf{PH}$ collapses to the second level.

Pf. Suffices to show $\Pi_2 \subseteq \Sigma_2$. $L \in \Pi_2$ implies $L$ expressible as:

\[L = \{x : \forall y \exists z (x, y, z) \in R\} \]

with $R \in \mathsf{P}$. $x\in L$ iff there is a circuit $C$ s.t.

\[\forall y[(x,y,z=C(x,y))\in R]. \]

Given $(x, y)$, "$\exists z (x, y, z) \in R$?" is in $\mathsf{NP}$. If SAT has poly-size circuits, there exists poly-time $C$ that can find $z$ for $\exists z(x,y,z)\in R?$. Just takes polynomial time to simulate $C$. Thus $L\in\Sigma_2$.

Thm (Shannon). With probability at least $1 - o(1)$, a random function

\[f:\{0,1\}^n \rightarrow \{0,1\} \]

requires a circuit of size $\Omega(2^n / n)$.

Pf. $B(n)=2^{2^n}=$ # functions $f:\{0,1\}^n\to\{0,1\}$.

On the other hand, # circuits with $n$ inputs and size $s$, is at most

\[C(n,s)\le(3(s+n)^2)^s. \]

So for $c<\frac{1}{2}$,

\[C(n,c2^n/n)\le (c'2^{2n}/n^2)^{c2^n/n}\\ \le O(1/n^2)2^{2c2^n}\\ <o(1)2^{2^n}. \]

Probability that a random function has a circuit of size $s=o(2^n/n)$ is at most

\[C(n,s)/2^{2^n}<o(1). \]

Rem. Frustrating fact: almost all functions require huge circuits. However, we still cannot find any $\mathsf{NP}$ problem that can be proved to have no polynomial size circuit.

Thm. $\mathsf{EXPSPACE\not\subset P/poly}$.

Pf. For every input length $n$, we find the "first" function $f_n$ which needs circuit of size $\Omega(2^n / n)$:

Enumerating all functions $\{0,1\}^n \rightarrow \{0,1\}$ takes $2^n$ space.
Then enumerate all circuits of size $O(2^n / n)$ and all inputs from $\{0,1\}^n$.

Then the language $L = \bigcup_n \{x \in \{0,1\}^n : f_n(x)=1\}$ is not in $\mathsf{P/poly}$. But it is in $\mathsf{EXPSPACE}$.

Further, we have:

Thm. $\mathsf{EXP^{\Sigma_2} \not\subset P/poly}$.

Pf. Find the "first" function $f_n$ which needs circuit of size $\Omega(2^n / n)$:

Given a function $f$ (whole size $2^n$), it's a $\mathsf{NP}$ problem to find an $O(2^n / n)$-size circuit that computes it. So given a $\mathsf{NP}$ oracle, we can check that all $O(2^n / n)$-size circuits cannot compute it.
Given a function "range" $[f_1, f_2]$, By a $\Sigma_2 = \mathsf{NP}^{\mathsf{NP}}$ oracle, we can check whether there is a function $f$ that needs $\Omega(2^n / n)$ size circuit in the range

\[(\exists f \in [f_1, f_2])(\forall C \text{ of size } O(2^n / n))(C \text{ does not compute } f). \]
A binary search over all $2^{2^n}$ functions with input length $n$ takes $2^n$ time.

Thm. $\mathsf{NEXP}^{\mathsf{NP}}\not\subset\mathsf{P/poly}$.

Pf. If $\mathsf{NEXP}^{\mathsf{NP}}\subset\mathsf{P/poly}$, then certainly $\mathsf{NP \subset P/poly}$, by Karp-Lipton Theorem, $\mathsf{PH}$ collapses to $\Sigma_2$. In particular, $\mathsf{P}^{\Sigma_2} = \Sigma_2 = \mathsf{NP}^{\mathsf{NP}}.$ By padding argument, $\mathsf{EXP}^{\Sigma_2} = \mathsf{NEXP}^{\mathsf{NP}}$, but we already know $\mathsf{EXP}^{\Sigma_2} \not\subseteq \mathsf{P/poly}$.

Parallelism

Def. The $\mathsf{NC}$ ("Nick's Class" after Nick Pippenger) hierarchy:

\[\begin{aligned} \mathsf{NC}^k &= O(\log^k n) \text{ depth, poly(n) size} \\ \mathsf{NC} &= \bigcup_k \mathsf{NC}^k \end{aligned} \]

Rem. It captures "efficiently parallelizable problems".

Ex. Boolean Matrix Multiplication:

Given $A,B,i,j$, output

\[(AB)_{i,j} = \vee_k (a_{i,k} \wedge b_{k,j}) \]

What is the parallel complexity of this problem? $\mathsf{NC}^1$

Construction:

level 1: compute $n$ ANDs: $a_{i,k} \wedge b_{k,j}$
next $\log n$ levels: tree of ORs.

We need to select the correct one and output from $n^2$ subtrees for all pairs $(i,j)$.

Trick: Multiplexers.

$2^k$ data inputs; $k$ control inputs ("selects"); $1$ output
Connects one of $2^k$ inputs to the output
“Selects” decide which input connects to output

Def. Boolean formula is a circuit whose graph is a tree, and we measure formula size by leaf-size.

Thm. $L \in \mathsf{NC}^1$ iff decidable by polynomial-size uniform family of Boolean formulas.

Pf.

($\Rightarrow$) Convert $\mathsf{NC}^1$ circuit into formula: recursively disassemble into a tree. #nodes in a tree bounded by $2^{O(\log n)} = \text{poly}(n)$.

($\Leftarrow$) Convert formula of size $n$ into formula of depth $O(\log n)$:

let $D$ be any minimal subtree with size $\geq n/3$. So its size $< 2n/3$.
do the following transformation, $C_1, C_0, D$ all size $\leq 2n/3$.

define $T(n) = \text{maximum depth required for any size } n \text{ formula}$. Then $T(n)\le T(2n/3)+3$, so $T(n)\le O(\log n)$.

Fact. $\mathsf{NC\subseteq P}$.

Fact. $\mathsf{NC}^1 \subseteq \mathsf{L}$.

Pf. On input $x$, compose logspace algorithms for:

generating $C_{|x|}$ with $O(\log n)$ depth
use DFS to evaluate the circuits $C_{|x|}(x)$

Fact. $\mathsf{NL\subseteq NC^2}$.

Pf. Only need to show that $\text{PATH}\in \mathsf{NC}^2$.

Given $G = (V, E)$, and vertices $s, t$. Let $A$ be the adjacency matrix (with self-loops). Then $(A^n)_{i,j} = 1$ iff path of length $\leq n$ from node $i$ to node $j$. Compute with depth $O(\log n)$ tree of Boolean matrix multiplications, output entry $(s,t)$, so $O(\log^2 n)$ depth in total.

Open Problem. $\mathsf{NC\overset{?}{=}P}$.

A language is $\mathsf{P}$-complete if: it is in $\mathsf{P}$ and every language in $\mathsf{P}$ is logspace-reducible to it.

CIRCUIT-VALUE = $\{\langle C, x \rangle \mid C \text{ is a Boolean circuit and } C(x) = 1\}$ is $\mathsf{P}$-complete.

If a $\mathsf{P}$-complete problem is in $\mathsf{NC}$, then $\mathsf{P} = \mathsf{NC}$.

Def (NC Hierarchy).

\[\mathsf{NC}^1 \subseteq \mathsf{NC}^2 \subseteq \mathsf{NC}^3 \subseteq \ldots \subseteq \mathsf{NC}. \]

Thm (NC Hierarchy Collapses). If $\mathsf{NC}^i = \mathsf{NC}^{i+1}$, then $\mathsf{NC} = \mathsf{NC}^i$.

Alternation Circuits

Def. $\mathsf{AC}^i$ is defined similarly to $\mathsf{NC}^i$ except gates are allowed unbounded fan-in, that is, OR and AND gates can be applied to more than $2$ bits. Such gates can be simulated by $(\log k)$-depth gates of $2$ bits. So $\mathsf{NC}^i \subseteq \mathsf{AC}^i \subseteq \mathsf{NC}^{i+1}$.

Ex. $\mathsf{AC}^0$ : polynomial number of gates and constant depth.

Binary Number Addition: Add $a_na_{n-1}...a_0$ and $b_nb_{n-1}...b_0$ to get $c_{n+1}c_nc_{n-1}...c_0$.

We can see that

\[c_k = \bigvee_{0 \leq i < k} \left( a_i \wedge b_i \wedge \bigwedge_{i < j < k} (a_j \vee b_j) \right) \]

So Binary Number Addition is in $\mathsf{AC}^0$.

Parity function:

\[f(x_1, x_2, \ldots, x_n) = x_1 \oplus x_2 \oplus \ldots \oplus x_n \]

Thm [Furst, Saxe, Sipser 1981]. Parity $\notin \mathsf{AC}^0$.

Pf. Proved by the so-called Polynomial Method: Transfer constant depth circuits to low-degree polynomials.

To get Parity $\notin \mathsf{AC}^0$, show the following two statements is enough:

Let $C$ be a circuit of size $s$ and depth $d$, then $C$ is $99\%$ approximated by a polynomial of degree $(\log s)^{O(d)}$ over $\mathbb{Z}_3 = \{0, 1, -1\}$.
Parity cannot be $99\%$ approximated by a polynomial of degree $c \cdot n^{1/2}$ over $\mathbb{Z}_3$

For the first statement:

To approximate $x_1\vee x_2 \vee \ldots \vee x_n$, we choose $\Theta(\log s)$ different random $n$-vectors from $\mathbb{Z}_3^n$ $A_i=(a_{i1},...,a_{in})$ and use $1-\Pi_i(1-p^2_{A_i})$, where $p_{A_i}=a_{i1}x_1+a_{i2}x_2+...+a_{in}x_n$. If $x_1\vee x_2 \vee \ldots \vee x_n=1$, $\text{Pr}_{A_i}[p_{A_i}=0]\le \frac{1}{3}$, so $\text{Pr}[1-\Pi_i(1-p^2_{A_i})=0]\le \frac{1}{3}^{\Theta(\log s)}\le 1/100s$.
Similarly, we can change every OR, AND, NOT gate to an $O(\log s)$-degree polynomial with error probability $\le 1/100s$. Therefore, finally, the total degree is $(\log s)^{O(d)}$ and the error probability is $\le1\%$. Then there is a set of vectors $A$ so that the polynomial equals $C$ for $99\%$ of the input.

For the second statement:

We can transfer any polynomial from $\{0,1\}^n \rightarrow \{0,1\}$ to $\{-1,1\}^n \rightarrow \{-1,1\}$ with the same degree

\[\begin{align*} & f(x_1, x_2, \ldots, x_n): \{0,1\}^n \rightarrow \{0,1\} \text{ is transferred to:} \\ & g(x_1, x_2, \ldots, x_n) = -f\left(-x_1-1, -x_2-1, \ldots, -x_n-1\right) - 1\text{ in }\mathbb{Z}_3 \end{align*} \]

Then the Parity function defined on $\{-1,1\}^n \rightarrow \{-1,1\}$ is $x_1 \cdot x_2 \cdot \ldots \cdot x_n$.

By contradictory assumption, $x_1 \cdot x_2 \cdot \ldots \cdot x_n = q(x_1, x_2, \ldots, x_n)$ for some polynomial $q$ of degree $c \cdot n^{1/2}$ over a set $S \subseteq \{-1,1\}^n$ where $|S| \geq 0.99 \cdot 2^n$. In $\{-1,1\}^n$, $x_i = x_i^{-1}$, so$$\prod_{i\in S}x_i =q(x_1, x_2, \ldots, x_7) \cdot \prod_{i\notin S}x_i$$, that is, monomial of degree $d' > n/2$ can be transferred to a degree $(n - d') + c \cdot n^{1/2}$ polynomial.
Any function over $\{-1,1\}^n \rightarrow \{-1,1\}$ is equivalent to a polynomial of degree $n$ in $\mathbb{Z}_3$ (equivalent to a multi-linear polynomial, that is, sum of monomials in which the degree of every variable is $0$ or $1$). Then any function over $S\to\{-1,1\}$ is equivalent to a polynomial of degree $\frac{n}{2} + c \cdot n^{1/2}$. However, the number of former is $2^{0.99\times 2^n}$ while the number of latter is $3^{\sum_{i=0}^{n/2+c\cdot n^{1/2}}\binom{n}{i}}$. We can choose c small, so that the former is larger than the latter.

Rem. $\mathsf{AC}^0$ cannot even compute Parity. What about we add a gate for Parity (SUM module $2$)?

Def ($\mathsf{AC}$ with counters). $\mathsf{AC}^0[p]$: $\mathsf{AC}^0$ with module $p$ counter: output $[x_1+x_2+...+x_n\equiv 0\pmod p]$. $\mathsf{ACC}^0=\bigcup_p\mathsf{AC}^0[p]$.

What we have proved: $\text{Parity} \notin \mathsf{AC^0}[3]$. Generalized:

Thm. Let $p$ and $q$ be distinct primes, then $\text{MOD}_q\notin\mathsf{AC}^0[p]$.

We use Circuit Complexity to prove algorithm lower bound. Recall "$\mathsf{NP}$ does not have polynomial-size circuits" implies $\mathsf{P\neq NP}$. Best bound known: linear.

Thm [Williams 2010]. $\mathsf{NEXP}\not\subset\mathsf{ACC}^0$.

Thm [Ryan Williams 2014]. “Faster all-pairs shortest paths via circuit complexity”: APSP with $n^3/2^{\Omega\left(\sqrt{\log n}\right)}$ time.

Hardness in P

APSP-hardness

Prob (APSP). All pair shortest path (APSP): Given a real-weighted directed graph, find the distance between every two vertices.

Alg. Floyd-Warshall algorithm solves APSP with running time $O(n^3)$.

Alg. Dijkstra algorithm with Fibonacci heap solves APSP with running time $O(mn+n^2\log n)$.

Alg. SOTAs of APSP with integer edge weights in $[-M,M]$:

Problem	Running time	Authors
Any graph	$O(m n + n^2 \log \log n)$	Pettie 2004
Undirected unweighted APSP	$O(n^{\omega}) = O(n^{2.38})$	Seidel '95
Undirected APSP	$O(M n^{2.38})$	Shoshan-Zwick '99
Directed APSP	$O(M^{0.68} n^{2.58})$	Zwick '98
$(1 + \varepsilon)$-Approximate APSP	$O(n^{2.38} \log M / \varepsilon)$	Zwick '98
$M=n^3$ APSP	$O(n^3/\exp(\sqrt{\log n}))$	Williams 2014

Rem. No APSP algorithm in $O(n^{3-\delta})$ time for constant $\delta>0$ when $M=\Omega(n)$.

Open Problem. Is there a truly subcubic algorithm for APSP? i.e., runs in $O(n^{3-\delta} \cdot \text{polylog } M)$ time for constant $\delta > 0$.

Prob. Distance product (Min-Plus product): Given $A,B$, calculate $C$ so that $C_{ij}=\min_k\{a_{ik}+b_{kj}\}$.

Thm. APSP has truly subcubic algorithms iff MPP has truly subcubic algorithms.

$(\Rightarrow)$ Trivial.

$(\Leftarrow)$ If $W$ is an $n$ by $n$ matrix containing the edge weights of a graph. Then $W^n$ is the distance matrix.
By induction, $W^k$ gives the distances realized by paths that use at most $k$ edges. Thus: $\mathsf{APSP}(n) \leq \mathsf{MPP}(n) \log n$.

Prob. Negative triangle: is there a negative weight triangle?

Rem. In general, no $O(n^{3-\delta})$ time algorithm for constant $\delta > 0$ known.

Negative triangle $\Rightarrow$ Distance Product: calculate $A^2$ and check whether $(A^2)[i,j]+A[j,i]<0$ for some $i,j$.

Prob. Matrix multiplication verification: Given $n \times n$ matrices $A, B, C$, verify whether $A \cdot B = C$.

Alg. Freivalds' algorithm:

Generate an $n \times 1$ random $0/1$ vector $r$
Compute $P = A (B \cdot r) - C \cdot r$
Return "YES" if $P$ is all zero, otherwise return "NO"

Open Problems.

Does negative triangle problem have a truly subcubic time algorithm?
Does distance product have a truly subcubic verification algorithm?

Thm [Vassilevska, Williams 2010]. The following problem either all have truly subcubic time algorithms, or none of them do.

all pair shortest path
distance product
negative triangle
distance product verification
minimum weight cycle

Pf. Easy reduction: Negative Triangle, Min Weight Cycle, Distance Product verification $\Rightarrow$ Distance Product.

For Distance Product $\Rightarrow$ Negative Triangle:

Distance Product $\Rightarrow$ All-pair Negative Triangle (for all pair of vertices $i,j$, is there a $k$ such that $w(i,j) + w(j,k) + w(k,i) < 0$).
- For instance $(A,B)$ of distance product, construct the tripartite graph with vertex set $I\cup J\cup K$
- For $i\in I,j\in J,k\in K$, $w(j,k)=A[j,k],w(k,i)=B[k,i]$, simultaneous binary search for $w(i,j)$.
All-pair Negative Triangle $\Rightarrow$ Negative Triangle:
- Still consider the tripartite graph, split $I, J, K$ into pieces of size $s$.
- ```
For every triple I_x, J_y, K_z:
    while I_x, J_y, K_z has a negative triangle:
        find a negative triangle (i, j, k)
        C[i,j] ← k
        delete (i,j)
```
- Let $T(s)$ be the time needed to find a negative triangle from a graph of size $s$. Suppose $T(s)=n^{3-\delta}$, the total time of the above algorithm: $O((n/s)^3 + n^2) \cdot T(s))$. Letting $s=n^{1/3}$ gives $O(n^{3-\delta/3}).$

So far, Negative Triangle = Distance Product.

For Negative Triangle $\Rightarrow$ Min Weight Cycle:

If the edge weights in $G$ are in $[-M,M]$, add $8M$ to every weight, then edge weights are in $[7M,9M]$, so that $4$-cycle has weight $\ge 28M$, larger than any $3$-cycle $\le 27M$. Thus, by the algorithm for minimum weight cycle, we can find the minimum weight triangle.

Negative triangle $\Rightarrow$ Distance Product verification:

W.l.o.g. suppose $G$ is a tripartite graph $I \times J \times K$. For $i \in I, j \in J, k \in K$, $w(j,k) = A[j,k]$, $w(k,i) = B[k,i]$, $w(i,j) = C[i,j]$. Let
\[C'=\begin{bmatrix}-C^T & -\infty\\-\infty & -\infty\end{bmatrix},A'=\begin{bmatrix}A & \mathbb{I}\\-\infty & -\infty\end{bmatrix},B'=\begin{bmatrix}B & -\infty\\-C^T & -\infty\end{bmatrix}. \]
here the identity matrix $\mathbb{I}_{ij}=\begin{cases}0 & i=j\\\infty & i\neq j\end{cases}$. A negative triangle exists iff
\[\begin{align*} &\ (\exists i,j,k)(A[j,k]+B[k,i]<-C[i,j])\\ \Leftrightarrow &\ (\exists i,j)\left(\min_k\{A[j,k]+B[k,i]\}<-C^T[j,i]\right)\\ \Leftrightarrow &\ (\exists i,j)\left(\min\{(AB)[j,i],-C^T[j,i]\}\neq-C^T[j,i]\right)\\ \Leftrightarrow &\ (\exists i,j)((A'B')[j,i]\neq C'[j,i])\\ \Leftrightarrow &\ A'B'\neq C' \end{align*} \]

Then we can check existence of a negative triangle by verifying $C’=A’B’$.

SETH-hardness

Prob (OV). Orthogonal vector (OV): Given a set $S$ of $n$ vectors in $\{0,1\}^d$, for $d=O(\log n)$, are there $u,v \in S$ with $u \cdot v=0$?

Alg. Trivial $O(n^2\log n)$ time algorithm.

Alg [Abboud, Williams, Yu 2015]. $n^{2-\Omega\left(\frac{1}{\log (d / \log n)}\right)}$.

Conj. OV Conjecture: OV on $n$ vectors requires $n^{2-o(1)}$ time.

Conj. Exponential time hypothesis (ETH): 3-SAT require $2^{\delta n}$ time for some constant $\delta>0$.

Alg (Schöning's algorithm). Repeat the following procedure for $1.5^n$ times:

Pick random initial assignment $x$
While there is at least one unsatisfied clause and have done this $\leq n$ times:
a) Pick an arbitrary unsatisfied clause $c$
b) Flip the bit of a random $x_p$ in the clause

Analysis:

Given a fixed satisfying assignment $\alpha$, the prob. that $x$ differs from $\alpha$ by $k$ bits is $\binom{n}{k} 2^{-n}$.
When $x$ differs from $\alpha$ by $k$ bits, the prob. that every step we make a correct modification is $1/3$
- So after $k$ steps, the prob. of getting correct $\alpha$ is $\binom{n}{k} 2^{-n}\left(\frac{1}{3}\right)^k$
- Sum over $k$: $\sum_{k=0}^n \binom{n}{k} 2^{-n}\left(\frac{1}{3}\right)^k = \left(\frac{1}{2}(1 + \frac{1}{3})\right)^n=\frac{1}{1.5^n}$.

Alg. In the step 2, repeat for $3n$ times. And do the entire procedure for $\left(\frac{4}{3}\right)^n$ times.

Analysis:

Prob. that the difference from $j$ to $0$ in $j+2i$ steps is: ($i+j$ correct steps, $i$ wrong steps)

\[\binom{j+2i}{i}\frac{j}{j+2i}\left(\frac{1}{3}\right)^{i+j}\left(\frac{2}{3}\right)^i \geq \frac{1}{3}\binom{j+2i}{i}\left(\frac{1}{3}\right)^{i+j}\left(\frac{2}{3}\right)^i \]

Calculate the case that $i=j$, which is

\[\frac{1}{3}\binom{3j}{j}\left(\frac{1}{3}\right)^{2j}\left(\frac{2}{3}\right)^j=\left(\frac{1}{2}\right)^{j-o(j)} \]
Sums over $j$:

\[2^{-n} \sum_{j=0}^n \binom{n}{j}\left(\frac{1}{2}\right)^j = \left(\frac{3}{4}\right)^n \]

Conj. SETH: for every constant $\varepsilon>0$, there is a $k$ such that $k$-SAT cannot be solved in $2^{(1-\varepsilon)n} \cdot \text{poly}(m)$ time.

Alg [Schöning 1999]. But $k$-SAT has $O((2-2/k)^n)$ time algorithm.

Thm. If SETH, then OV.

Pf. Given a $k$-CNF (let $n$ be the number of variables and $m$ be the number of clauses), we partition the variables into $V_1, V_2$ on $n/2$ variables each. For all assignment $\phi,\psi$ of $V_1$, $V_2$, resp., construct $(m+2)$-vectors: the $i$-th position of the vector is $0$ if $\phi/\psi$ satisfy the $i$-th clause, $1$ otherwise.

Obviously, for an satisfying assignment of $k$-CNF, its partition on $V_1$ and $V_2$, $\phi$ and $\psi$, must satisfy all clauses. So the corresponding vectors of $\phi$ and $\psi$ are orthogonal.

So we have $N=2\cdot 2^{n/2}$ vectors with dimension $O(m)=O(n)$. If OV has an $N^{2-\delta}$ algorithm, we will have an $O(2^{n(1-\delta/2)})$ $k$-SAT algorithm.

Prob. Edit Distance: counting the minimum number of operations required to transform one string into the other.

Alg [Masek, Paterson 1980]. Edit distance can be computed in $O(n^2/\log n)$ time.

Thm. No $n^{2-\delta}$ time algorithm for edit distance under OV conjecture.

Prob. Diameter: Let $d(u,v)$ be the distance from $u$ to $v$ in the graph $G$. Calculate the diameter $D(G)=\max_{u,v\in G}d(u,v)$.

Alg. Trivial way: finding all-pair distances. BFS from all vertices, $O(nm)$.

Thm [Roditty, V. Williams 2014]. The diameter of unweighted graphs can be $\frac{3}{2}$-approximated in $\tilde{O}(mn^{1/2})$ time.

Pf. First we randomly sample a vertex set $S$ by including every vertex with probability $1/\sqrt{n}$ independently. With prob. $1-\frac{1}{n^c}$, $|S|=O(\sqrt{n}\log n)=\tilde{O}(\sqrt{n}).$

For every vertex $u$, compute $d(u, S)=\min_{v \in S} d(u, v)$: BFS from all vertices of $S$. Time: $\tilde{O}(m \sqrt{n})$.

Find the vertex $w$ that maximizes $d(w, S)$, and find the ball $T = \{v : d(w, v) < d(w, S)\}$. With high probability, $|T|=\tilde{O}(\sqrt{n})$.

Run BFS from vertices in $S$ and $T$, and return the longest distance. Total Time: $\tilde{O}(m \sqrt{n})$.

Approximation analysis:

Consider the real diameter $D = d(a, b) = 3h$. If there is a vertex $u \in S$ such that either:

$d(u, a) \geq 2h$ or $d(u, b) \geq 2h$
$d(u, a) \leq h$ or $d(u, b) \leq h$

Then the BFS from $u$ can get a $\frac{3}{2}$-approximation. What's left is, for all $u \in S$, $h < d(u, a) < 2h$ and $h < d(u, b) < 2h$. This means $d(a, S) > h$ so $d(w,S)>h$.

Since $w \in T$, if $d(w, b) \geq 2h$, we can also find a $\frac{3}{2}$-approximation by BFS. Otherwise, $d(w, b) < 2h$. Since $d(w, S) > h$, the vertex $y$ on the path from $w$ to $b$ with distance $h$ from $w$ must be in $T$. Since $d(w, y) = h$, $d(y, b) < h$, so $d(a, y) > 2h$. We can get a $\frac{3}{2}$-approximation by BFS from $y$.

Thm [Roditty, V. Williams 2014]. No $O(m^{2-\delta})$ time algorithm can compute the diameter better than $\frac{3}{2}$-approximation under OV conjecture.

Pf. For OV instance $(A,B)$, construct a graph with vertex set $A\cup B\cup[d]\cup\{x,y\}$. Connect $(u,x),(x,i),(i,y),(y,v)$ for all $i\in [d],u\in A,v\in B$. Connect $(u,i)$ if $u_i=1$, $(j,v)$ if $v_j=1$.

If $(u,v)$ are orthogonal, their distance is $3$ ($u\to x\to y\to v$). Otherwise, their distance is $2$ ($u\to i\to v$). Thus, if we can distinguish $2$ or $3$ for diameter, we can solve OV.

Prob. Single Source Reachability:

Input: a directed graph $G$, a source node $s$;
Updates: Add or remove edges;
Query: #SSR How many nodes can $s$ reach?

Alg. Trivial: $O(m)$ time depth-first search.

Thm [Abbound, V. Williams 2014]. If dynamic #SSR can be solved in $O(m^{1-\delta})$ time (both update and query time), then orthogonal vector can be solved in truly subquadratic time, (then SETH fails).

Pf. For OV instance $(A,B)$, at the beginning, construct a graph with vertex set $\{s\}\cup[d]\cup B$. Connect $(i,v)$ if $v_i=1$. For some $u\in A$, add an edge from $s$ to $i$ iff $u_i=1$. Then $u\cdot v=0$ iff $s$ cannot reach $v$.

for every v∈B
	add edges (i,v) iff b[i]=1 
for all u∈A
	add edges (s,i) iff a[i]=1
 	if #SSR(s) < n + (1s in u)
 		return YES
 	remove all edges from s
return NO

Analysis: $O(nd)$ updates, the graph has $O(nd)$ edges, $O(n)$ queries. If update and query time is $O(m^{1-\delta})$ for constant $\delta>0$, which will be $\tilde{O}(n^{1-\delta})$ here, then OV can be solved in $\tilde{O}(n^{2-\delta})$ time

3SUM-hardness

Prob (3SUM). 3SUM: Given a set $S$ of integers, $|S|=n$ are there $a,b,c \in S$ so that $a+b+c=0$ ?

Alg. Use two pointers to solve 3SUM with $O(n^2)$ time.

Alg [Baran, Demaine, Pătraşcu 2005]. $\sim n^2 / \log^2 n$ time algorithm for integers.

Alg [Granlund, Pettie 2014]. $\sim n^2 / \log n$ time algorithm for real numbers.

Conj. 3SUM Conjecture: 3SUM on $n$ integers in $\left\{-n^3, \ldots, n^3\right\}$ requires $n^{2 - o(1)}$ time.

Thm [Gajentaan, Overmars 1995]. Many computational geometry problems are 3SUM-hard to get $O(n^{2-\delta})$ time algorithm:

Given $n$ points in plane, are there $3$ in a line?
Given $n$ lines in plane, are there $3$ pass through one point?
Given $n$ strips in the plane, does their union contain a given rectangle
Given $n$ triangles in the plane, does their union contain another given triangle
$\ldots$

Pf. For 3SUM instance $S$, for every $a\in S$, create a point $(a,a^3)$ in plane.

Claim: $a+b+c=0$ iff $(a, a^3), (b, b^3), (c, c^3)$ are collinear.

Thm [Pătraşcu 2010]. Find $O(n^{o(1)})$ time update/query time algorithm for many dynamic problems is 3SUM-hard:

dynamic reachability
subgraph connectivity
Langerman’s problem
$\ldots$

posted @ 2025-03-04 20:12 xcyle 阅读(135) 评论(0) 收藏举报

刷新页面返回顶部

Problem	Running time	Authors
Any graph	\(O(m n + n^2 \log \log n)\)	Pettie 2004
Undirected unweighted APSP	\(O(n^{\omega}) = O(n^{2.38})\)	Seidel '95
Undirected APSP	\(O(M n^{2.38})\)	Shoshan-Zwick '99
Directed APSP	\(O(M^{0.68} n^{2.58})\)	Zwick '98
\((1 + \varepsilon)\)-Approximate APSP	\(O(n^{2.38} \log M / \varepsilon)\)	Zwick '98
\(M=n^3\) APSP	\(O(n^3/\exp(\sqrt{\log n}))\)	Williams 2014

xcyle

Theory of Computation

Model of Computation

Mathematical Logic

Statement logic

Formal Statement Calculus - L

Components:

Axioms:

Rules of Deduction:

First-order logic

Formal system \(K_{\mathcal{L}}\)

Axioms

Rules

Finite Automata & Context Free Grammar

DFA, NFA and Regular language

Language, machine and DFA

Closure properties

Nondeterministic Finite Automata

Equivalence of NFA and DFA

Closure properties

Regular Expressions

CFG and PDA

Context Free Grammar

Pushdown Automaton

Pumping Lemma

Nonregular Languages

Non context-free Languages

Turing Machine

DTM, NTM, and Variants

Standard Turing machine

Multitape Turing Machines

Nondeterministic T.M.s

TM with outputs

Reducibility

Gödel’s Entscheidungsproblem

Halting Problem

The Post Correspondence Problem

Reductions via computation histories

Mapping reducibility

Recursion Theorem

*Kolmogorov complexity

Complexity

Cell-Probe Model

“Were-you-last?” Game

Comparison-based Sorting

Information Retrieval Problem

Dynamic Partial Sum

Deterministic & Nondeterministic

Time Complexity

Space Complexity

Logarithmic Space

NL-completeness

Polynomial Time/Space

Padding Argument

PSPACE-completeness

Polynomial-Time Hierarchy

Relativization

Exponential Time

Randomized Computation

Probabilistic TM

Additive Spanner

Primality test

Randomized Complexity Classes

Polynomial Identity Testing

Perfect Matching

Matrix Multiplication

Interactive Proof

Proof Systems

Graph Isomorphism

Arthur-Merlin Games

Multiprover Interactive Proofs

Decision Trees

Circuit Complexity

Circuit Families

Parallelism

Alternation Circuits

Hardness in P

APSP-hardness

SETH-hardness

3SUM-hardness