NLP 之三：Transformer

编码器-解码器（Encoder-Decoder）

以机器翻译为例，输入不定长向量 \(\bm{x}\)，希望得到其翻译 \(\bm{y}\)，同样是不定长向量。

我们希望将 \(\bm{x}\) 输入编码器得到定长背景信息 \(\bm{c}\)，将 \(\bm{c}\) 输入解码器得到 \(\bm{y}\)。

考虑让编码器和解码器都是RNN，对应的时间步就是 \(\bm{x}\) 和 \(\bm{y}\) 的各个维度。编码器的隐藏状态 \(\bm{h}_t\) 由 \(\bm{h}_{t-1}\) 和 \(\bm{x}_t\) 决定；解码器的隐藏状态 \(\bm{s}_t\) 由 \(\bm{s}_{t-1}\)，\(\bm{y}_{t-1}\) 和 \(\bm{c}\) 决定。

在监督学习中，可以直接将真实的标签序列输入到decoder中，这被称为强制教学（teacher forcing）。

实际部署时，我们希望用预测不定长文本，但是如果只是每次取出概率最大的预测结果，不一定能让整个向量成为概率最大的向量（这种方法称之为贪婪搜索）。一个代替的办法是束搜索，我们需要设定一个超参数 \(k\)，每次保留概率前 \(k\) 大的预测结果，下一步从这 \(k\) 个候选序列再生成的所有序列中选出概率最大的 \(k\)个。

注意力机制

在文本翻译中，翻译出的单个位置很可能只由原序列的几个特定位置决定。为了让模型可以注意到这些位置，注意力机制被提出。

注意力（Attention）

注意力机制为每个时间步 \(t'\) 分配一个自己的背景信息 \(\bm{c}_{t'}\)。为了计算它，每个时间步 \(t\) 会被分配三个变量 \(\bm{q}_t,\bm{k}_t,\bm{v}_k\)，分别称之为查询（query）项，键（key）项和值（value）项，其具体取值暂时按下不表。

背景信息 \(c_{t'}\) 的计算方式是用所有时间步的值项加权平均，即有概率分布 \(p_{t',t}\)，使得 \(c_{t'}=\sum\limits_{t}p_{t',t}\bm{v}_t\)。进一步，我们通过用 \(t'\) 的查询项 \(\bm{q}_{t'}\) 和每个位置的键项 \(\bm{k}_t\) 匹配（做点积，为了梯度稳定可以除个 \(\sqrt{d}\)），然后softmax得到 \(p_{t'}\)。

具体来说，我们令 \(\bm{Q}\in \mathbb{R}^{1\times d}\) 等于 \(\bm{s}_{t'-1}\)，\(\bm{K}\in\mathbb{R}^{d\times T}\) 第 \(i\) 列为 \(\bm{h}_t^T\)，\(\bm{V}\in\mathbb{R}^{T\times d}\) 第 \(i\) 行为 \(\bm{h}_t\)，那么有

\[\bm{c}_{t'}=\textup{softmax}\left(\frac{\bm{QK}}{\sqrt{d}}\right)\bm{V} \]

这样为每个时间步 \(t'\) 求出了背景信息 \(\bm{c}_{t'}\)，用它和 \(\bm{s}_{t'-1}\)，\(\bm{y}_{t'-1}\) 共同决定 \(\bm{s}_{t'}\)。

值得一提的是，注意力机制的一个特点是便于并行计算。

自注意力（Self-Attention）

当我们只希望捕捉某个序列 \(\bm{x}\) 自身的信息时，可以用注意力的另外一种形式代替它——自注意力。

在自注意力中，仍有 \(\bm{c},\bm{Q},\bm{K},\bm{V}\) 的结构，只不过它们都直接由 \(\bm{x}\) 生成，例如使用单层MLP（不同时间步的参数相同）。

多头（Multi-Head）

为了全方面的注意到序列的信息，我们可以将 Attention 和 Self-Attention 中的结构复制若干份，分别计算最终合并。

这样的方法称之为 Multi-Head Attention 和 Multi-Head Self-Attention。每一份被看作一个 Head。

Transformer

最后我们介绍非常经典的工作 transformer，许多大模型都基于transformer的结构。

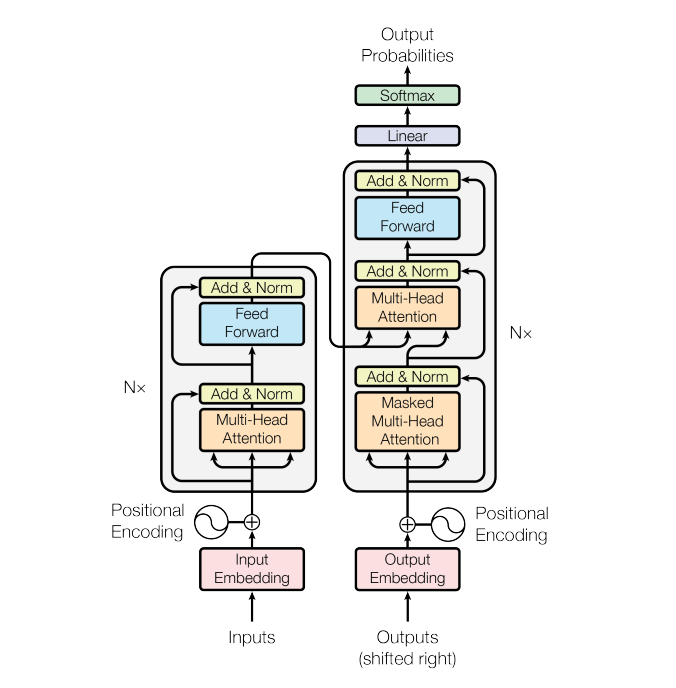
从宏观的角度看，transforer 仍然是 Encoder-Decoder 的结构，而 Encoder 由若干 Encoder Block 组成，Decoder 由若干 Decoder Block 组成。在两种 Block 内部，Self-Attention 都作为主要结构出现。如下图所示。

Embedding

在之前的若干模型中，如 RNN，模型本身已经描述了输入序列 \(\bm{x}\) 的位置信息。因此我们只需要将序列每个词转化为词向量作为输入。

而在 Self-Attention 中 \(\bm{x}\) 的每个位置是等价的，也就是说每个词的位置信息丢失了。为此，我们在将 \(\bm{x}\) 转化为词向量时，需要同时考虑其位置信息的影响。因此这里的 word embedding 需要额外考虑其位置编码，称之为 positional embedding。

具体来说，第 \(i\) 个位置的位置向量 \(\bm{p}_t\) 也将是一个长度为 \(d\) 的向量。一个位于 \(p\) 的词经过 word embedding 的结果是其对应的长度为 \(d\) 的词向量加上 \(\bm{p}_t\)。一个十分精巧的构造是：

\[\bm{p}_{t,i}= \left\{ \begin{array}{l} \sin(t/10000^{2k/d}) &i=2k \\ \cos(t/10000^{2k/d}) &i=2k+1 \end{array} \right. \]

首先可以发现当向量维度 \(i\) 变大时，三角函数的频率递减。这其实很像用进制表示，每一维对应了进制下的一位。

另外一个最直接的好处就是，由于三角函数的合角公式，存在和 \(t\) 无关的矩阵 \(\bm{M}_{\delta}\) 使得

\[\begin{bmatrix} \sin t \\ \cos t \end{bmatrix} \bm{M}= \begin{bmatrix} \sin (t+\delta) \\ \cos (t+\delta) \end{bmatrix} \]

这样一来，模型可以在每个位置通过这种PE找到和其任意距离的位置。

Encoder

接下来我们会详细考察 Encoder Block 和 Decoder Block 的内部结构。

观察上图，一个 Encoder Block 大致可以分为两部分，第一部分是一次 Multi-Head Attention 和 Add&Norm，第二部分是一次 Feed Forward 和 Add&Norm。

Multi-Head Attention 是上文的多头（自）注意力；Add&Norm 是残差连接+层归一化。Feed Forward 是一个前馈神经网络，其具体内容为全连接\(\rightarrow\)ReLU\(\rightarrow\)全连接，即

\[\textup{FeedForward}(X)=W_2\textup{ReLU}(W_1X+b_1)+b_2 \]

因此两部分分别为

\[\textup{LayerNorm}\left(X+\textup{MultiHeadAttention}(X)\right) \]

\[\textup{LayerNorm}\left(X+\textup{FeedForward}(X)\right) \]

Decoder

一个 Decoder Block 分为三部分，第一部分是 Masked Multi-Head Attention 和 Add&Norm，第二部分是 Multi-Head Attention 和 Add&Norm，第三部分是 Feed Forward 和 Add&Norm。注意在所有 Decoder Block 之后还有一次单层 softmax。

其中唯一特殊的一点是 "Masked" Multi-Head Attention。这里的 masked 指的是会用一个位掩码矩阵将 Self-Attention 中所有位置对后文的查询掩盖掉，即将 \(\bm{QK}\) 乘积主对角线上方全部置为 \(0\)。这是因为训练时 teacher forcing 的存在，不能让模型直接获取答案。

另外在第二部分中，Self-Attention 所需的矩阵 \(\bm{K}\) 和 \(\bm{V}\) 是由 Encoder 最终的背景变量 \(\bm{c}\) 计算得到，\(\bm{Q}\) 则是根据上一个 Decoder Block 的隐藏状态得到。