PCA主成分分析

 

一、数学原理

PCA的数学原理参见这条博客，写的通俗易懂：http://blog.codinglabs.org/articles/pca-tutorial.html

 

其中几个重点步骤如下：

 

 

 

 

 

 

二、除了降维之外的综合评价打分体系应用

 

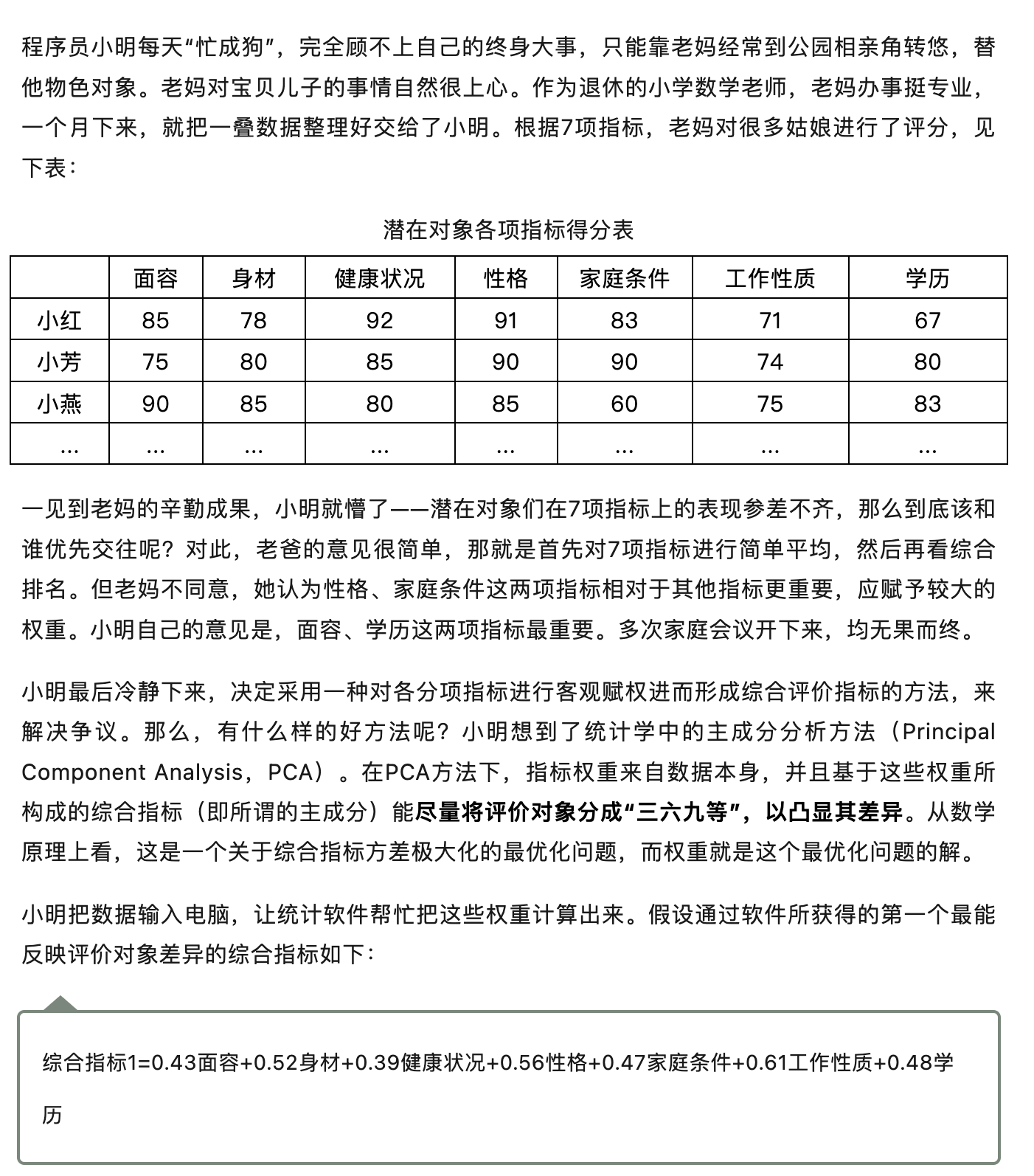
PCA主要被用于降维，但是总是记得之前数学建模的时候可以被用来作为综合评价打分体系，找了半天还是这个例子最形象的解释了怎么用PCA去综合评价打分：https://mp.weixin.qq.com/s?__biz=MzUyMzUxMTUyMw==&mid=2247485437&idx=1&sn=5604eee840dc6ba34e26ac839cc7a932

 

最关键的一句话：综合指标就是所谓的主成分！

 

 

 

 三、程序的代码实现

 

python中的sklearn库中有现成的PCA库

 

#导入所需的库和模块：
import pandas as pd
from sklearn.decomposition import PCA

#从数据集中提取出特征指标列，即去掉“belong_uid”列：

features = data_test.drop('belong_uid', axis=1)

#对特征指标进行标准化处理，使得每个指标的均值为0，方差为1：

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
features_standardized = scaler.fit_transform(features)

#使用PCA模型对标准化后的特征指标进行降维，得到主成分：

pca = PCA()
principal_components = pca.fit_transform(features_standardized)

#将主成分合并回原始数据集，并计算每个用户的综合评价得分：
data_test['score'] = principal_components.sum(axis=1)

 

 

 这里踩坑有以下几点：

1.PCA 类的主要参数：

  • n_components: int,float　　n 为正整数，指保留主成分的维数；n 为 (0,1] 范围的实数时，表示主成分的方差和所占的最小阈值。
 n_components must be between 0 and min(n_samples, n_features)=1 with svd_solver='full'

 

主成分不能超过特征的数量，即K<=N很好理解，毕竟PCA是降维，不能增维，但是不能超过样本数量这里绕了很久，比如一个数据集只有两个样本，但是有7个特征，这个数据集最多只能有两个主成分，自己总结的笔记如下： 

 

 

所以除非有明确确定的主成分数量，否则代码一般推荐都是pca = PCA（）,再去拟合数据，否则人工强行定义的n_components很可能不在between 0 and min(n_samples, n_features) 范围内

pca = PCA()

data_pca = pca.fit_transform(data)

 

2.PCA 类的主要属性：

  • components_： 　　方差最大的 n-components 个主成分
  • explained_variance_：　　各个主成分的方差值
  • explained_variance_ratio_：　　各个主成分的方差值占主成分方差和的比例

 

3.主成分到底是什么：

举例子：data_std是一个9行7列的dataframe结构的数据集，每行是一个样本数据，7列表示7个特征，请问在python中这行代码：data_pca = pca.fit_transform(data_std) 得到的data_pca是什么

 

在Python中，如果我们使用PCA模型对一个9行7列的DataFrame数据集data_std进行拟合和转换，那么得到的data_pca将是一个9行k列的数组，其中k是我们指定的主成分数量。每一行表示一个样本的综合评价得分，每一列表示一个主成分的得分。

 

from sklearn.decomposition import PCA

# 创建PCA模型，指定主成分数量为3
pca = PCA(n_components=3)

# 对数据进行拟合和转换
data_pca = pca.fit_transform(data_std)

# 输出data_pca
print(data_pca)

 运行这段代码，我们可以得到一个9行3列的数组，表示每个样本在3个主成分上的得分，如果将这三列加起来，就是每个样本的主成分的得分总和

 

4.python主成分的可视化：

https://developer.aliyun.com/article/947661

 

posted @ 2023-04-11 11:11  阿井井w  阅读(202)  评论(0)  编辑  收藏  举报