支持向量机
硬间隔:
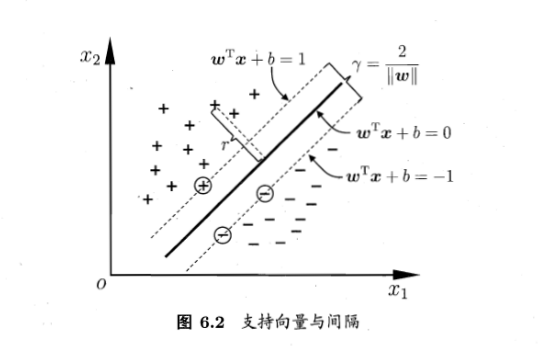
超平面通过如下方程描述:
$w^{T}x+b=0$
则任意一点到超平面的距离:
$r=\frac {|w^{T}x+b|} {||w||}$
假设超平面(w,b)能将训练样本正确分类,即对于$(x_{i},y_{i})\subset D$,若$y_{i}=+1$,则有$w^{T}x_{i}+b>0$,若$y_{i}=-1$,则有$w^{T}x_{i}+b<0$。令
$\left\{\begin{matrix}w^{T}x_{i}+b \geq 1,y_{i}=+1\\ w^{T}x_{i}+b \leq 1,y_{i}=-1\end{matrix}\right.$
因为$w^{T}x+b$前面可以乘以一个常数而超平面不变,所有令$w^{T}x+b=1$,则最大化
$\gamma = \frac {2}{||w||}$
即:
$\underset{w,b}{max} \frac {2}{||w||}$
$s.t. \ y_{i}(w^{T}x_{i}+b)\geq 1,i=1,2,...,m$
等价于:
$\underset{w,b}{min} \frac {1}{2}||w||^{2}$
$s.t. \ y_{i}(w^{T}x_{i}+b)\geq 1,i=1,2,...,m$
对偶问题:
$L(w,b,a)=\frac{1}{2}||w||^{2}+\sum_{i=1}^{m}a_{i}(1-y_{i}(w^{T}x_{i}+b))$
对w和b求导:
$w=\sum_{i=1}^{m}a_{i}y_{i}x_{i}$
$0=\sum_{i=1}^{m}a_{i}y_{i}$
把上式代入$L(w,b,a)$ 得:
$\frac{1}{2}(\sum_{i=1}^{m}a_{i}y_{i}x_{i})^{2}+\sum_{i=1}^{m}a_{i}-\sum_{i=1}^{m}a_{i}y_{i}x_{i}\sum_{i=1}^{m}a_{i}y_{i}x_{i}-\sum_{i=1}^{m}a_{i}y_{i}b$
$=\sum_{i=1}^{m}a_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_{i}a_{j}y_{i}y_{j}x_{i}x_{j}$
再根据拉格朗日对偶性:
$\underset{a}{max}\sum_{i=1}^{m}a_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_{i}a_{j}y_{i}y_{j}x_{i}x_{j}$
$s,t, \ \sum_{i=1}^{m}a_{i}y{i}=0,a_{i}\geq 0,i=1,2...m$
解出$a$后,求出$w,b$即可得到模型:
$f(x)=w^{T}x+b=\sum_{i=1}^{m}a_{i}y_{i}x_{i}^{T}x+b$
核函数:
样本是线性不可分的,那么可以将样本从原始空间映射到一个更高维的空间,使得样本线性可分。所以线性模型表示为:
$f(x)=w^{T}\phi(x)+b$
即目标函数为:
$\underset{w,b}{min}\frac{1}{2}||w||^{2}$
$s.t. \ y_{i}(w^{T}\phi (x_{i})+b)\geq 1,i=1,2,...,m$
对偶问题:
$\underset{a}{max}\sum_{i=1}^{m}a_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_{i}a_{j}y_{i}y_{j}\phi (x_{i})\phi (x_{j})$
$s,t, \ \sum_{i=1}^{m}a_{i}y{i}=0,a_{i}\geq 0,i=1,2...m$
求解上式涉及到$\phi (x_{i})\phi (x_{j})$,这是样本$\phi (x_{i}),\phi (x_{j})$映射到特征空间之后的内积,由于特征空间维数可能很高,甚至可能是无穷维,因此直接计算$\phi (x_{i})\phi (x_{j})$通常是困难的,因此设想这样的函数:
$\kappa(x_{i},x_{j})=<\phi (x_{i}),\phi (x_{j})>=\phi (x_{i})\phi (x_{j})$
因此对偶问题可以重写为:
$\underset{a}{max}\sum_{i=1}^{m}a_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_{i}a_{j}y_{i}y_{j}\kappa(x_{i},x_{j})$
$s,t, \ \sum_{i=1}^{m}a_{i}y{i}=0,a_{i}\geq 0,i=1,2...m$

组合核函数:
1.若$\kappa_{1},\kappa_{2}$为核函数,则对于任意的正数$\gamma_{1},\gamma_{2}$,其线性组合$\gamma_{1}\kappa_{1}+\gamma_{2}\kappa_{2}$也是核函数。
2.若$\kappa_{1},\kappa_{2}$为核函数,则核函数的直积$\kappa_{1}\otimes \kappa_{2}(x,z)=\kappa_{1}(x,z)\kappa_{2}(x,z)$也是核函数。
3.若$\kappa_{1}$为核函数,则对于任意函数$g(x)$,$\kappa(x,z)=g(x)\kappa_{1}(x,z)g(z)$也是核函数。
软间隔与正则化:
上面是假设训练样本在样本空间或特征空间中是线性可分的,即存在一个超平面能将不同类的样本完全分开,然而现实中往往很难确定合适的核函数将不同类的样本完全分开。于是引进“软间隔”。运行一些不符合条件的样本。即$y_{i}(w^{T}x_{i}+b)< 1$

即目标函数为:
$\underset{w,b}{min}\frac{1}{2}||w||^{2}+C\sum_{i=1}^{m}\iota_{0/1}(y_{i}(w^{T}x_{i}+b)-1)$
其中$C>0$是一个常数,$\iota_{0/1}$是损失函数:
$\iota_{0/1}(z)=\left\{\begin{matrix}1,if\ z<0\\ 0,otherwise\end{matrix}\right.$
因为$\iota_{0/1}$不连续,数学性质不好,不太容易求解,可以使用其他损失函数:
hinge损失函数:$\iota_{hinge}(z)=max(0,1-z)$
指数损失函数:$\iota_{exp}(z)=exp(-z)$
对率损失函数:$\iota_{log}(z)=log(1+exp(-z))$
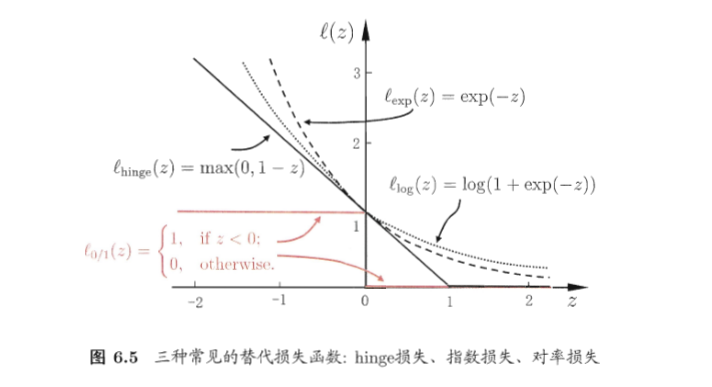
若采用hinge损失函数则:
$\underset{w,b}{min}\frac{1}{2}||w||^{2}+C\sum_{i=1}^{m}max(0,1-y_{i}(w^{T}x_{i}+b))$
引入松弛变量$\xi_{i}\geq 0$则:
$\underset{w,b}{min}\frac{1}{2}||w||^{2}+C\sum_{i=1}^{m}\xi_{i}$
$s.t. \ y_{i}(w^{T}x_{i}+b)\geq 1-\xi_{i},\ \xi_{i}\geq 0,i=1,2,...,m$
拉格朗日函数,其中$a_{i}\geq 0,\mu_{i}\geq 0$是拉格朗日乘子:
$L(w,b,a,\xi,\mu)=\frac{1}{2}||w||^{2}+C\sum_{i=1}^{m}\xi_{i}+\sum_{i=1}^{m}a_{i}(1-\xi_{i}-y_{i}(w^{T}x_{i}+b))-\sum_{i=1}^{m}\mu_{i}\xi_{i}$
求导得:
$w=\sum_{i=1}^{m}a_{i}y_{i}x_{i}$
$0=\sum_{i=1}^{m}a_{i}y_{i}$
$C=a_{i}+\mu_{i}$
代入拉格朗日函数得对偶问题:
$\underset{a}{max}\sum_{i=1}^{m}a_{i}-\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}a_{i}a_{j}y_{i}y_{j}x_{i}x_{j}$
$s,t, \ \sum_{i=1}^{m}a_{i}y{i}=0,0\leq a_{i}\leq C,i=1,2...m$



