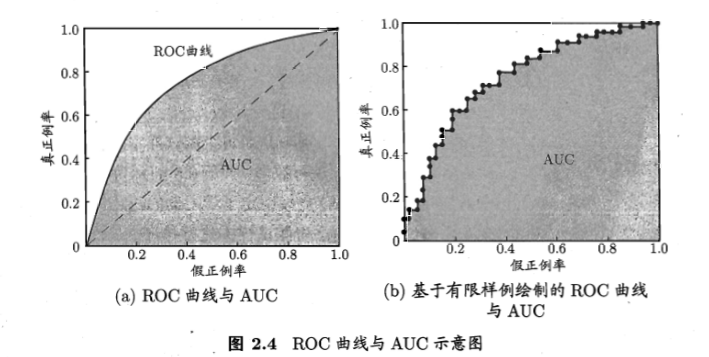
混淆矩阵

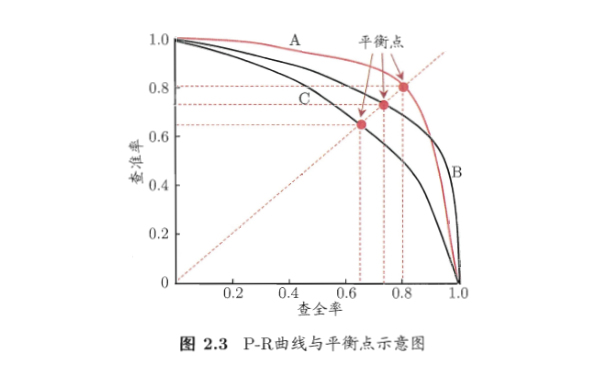
P-R图直观的显示出学习器在样本总体上的查全率和查准率，在进行比较时，若一个学习器的P-R曲线被另一个学习器的曲线完全包住则后者的性能优于前者，比如A比C好。

如果发生交叉现象则可以用F1度量（P-R曲线比ROC曲线适合不平衡样本）：

　　　　　　　　$F1=\frac{2   P   R}{P + R}$

一般形式（表达出对查准率/查全率的不同偏好）：

　　　　　　　　$F_{\beta}=\frac{(1 + \beta^{2})  P   R}{(\beta^{2}   P) + R}$       

$F_{\beta}$是加权调和平均：

　　　　　　　　$\frac{1}{F_{\beta}}=\frac{1}{1 +  \beta^{2}} (\frac{1}{P} + \frac{\beta^{2}}{R})$    

其中$\beta>0$度量了查全率对查准率的相对重要程度，$\beta=1$退化为标准的F1，$\beta>1$时查全率有更大影响，$\beta<1$查准率有更大的影响。

 

很多时候我们有多个二分类混淆矩阵，甚至是执行多分类任务，每俩俩类别的组合都对应一个混淆矩阵，总之我们希望在n个二分类的混淆矩阵上综合考察查准率和查全率。

1.计算P、R、F1的平均值

2.计算TP、FP、TN、FN的平均值，再计算P、R、F1。

 

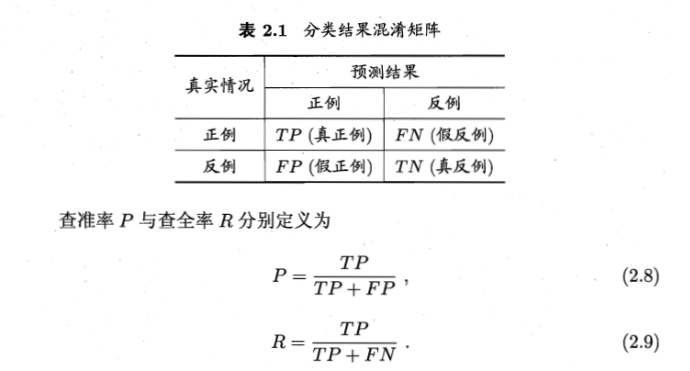
ROC和AUG：很多学习器是为ce测试样本产生一个实值或概率预测，然后将这个预测值与一个分类阈值进行比较，若大于阈值则为正类，否则为反类。

真正例率（纵坐标）：

　　　　　　　　$TPR=\frac{TP}{TP + FN}$

假正例率（横坐标）：

　　　　　　　　$FPR=\frac{FP}{TN + FP}$

绘图：

给定m+个正例和m-个反例，根据学习器预测结果对样例进行排序，然后把分类阈值设为最大，即把全部样例均预测为反例。此时真正例率和假反例率均为0，然后将分类阈值依次设为每一个样例的预测值，即依次将每个样例划分为正例。

进行学习器的比较时，与P-R图类似，若一个学习器的ROC曲线被另一个学习器的曲线完全包住则后者的性能优于前者。若发生交叉则比较俩者的面积即AUG。

$AUG \approx \frac{1}{2} \sum_{i = 1}^{m - 1} (x_{i + 1} - x_{i}) (y_{i} + y_{i + 1})$