P3800 power收集 题解

P3800 Power收集 题解

传送门

前排声明:蒟蒻刚学oi没多久,写的可能比较粗糙,望谅解

大致题意

给一个\(N×M\)大小的矩阵

其中有k个点包含一个带有价值的P点

每一行中的一个格子i都可以从上一行中的第\([i-t,i+t]\)个格子中转移过来

求可以获得的最大价值

分析

大致思路和P1725 琪露诺很像,只是换了一种形式而已

既然每一个格子\(i\)都可以从上一行中的第$ [i-t,i+t] $个格子中转移过来

我们设\(a[i][j]\)为第\(i\)行第\(j\)个点的价值大小

容易得到状态转移方程:

• \(dp[i][j]=max(dp[i-1][k])+a[i][j] (j-T<=k<=j+T)\)

• 因此,对于每一个\(dp[i][j]\)来说

他的值均是由上一行中\([j-t,j+t]\)区间中的最大值转移过来的

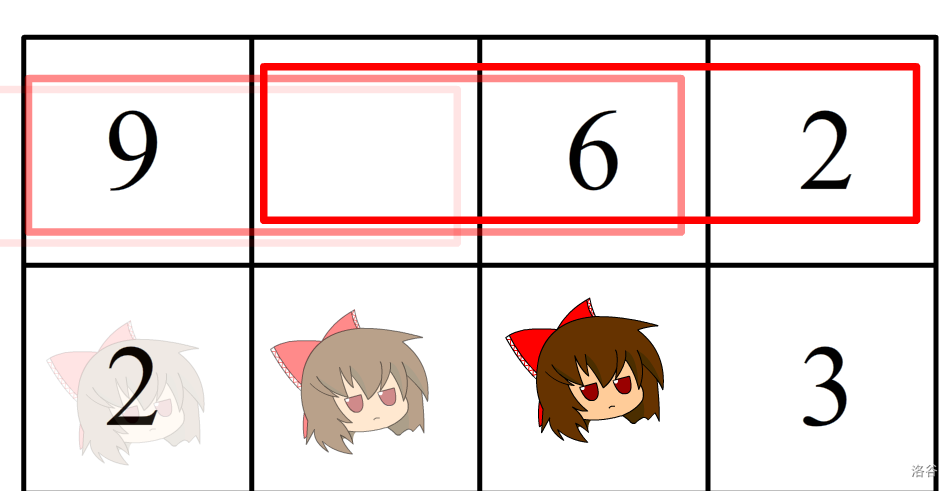
(懒得找城管的图了,只好拿之前cirno的图改了一下)

可以看出这是一个滑动区间求最值的问题

可以考虑用单调队列来优化

在进行第\(i\)行第\(j\)列的转移前

利用滑动窗口将第\(i-1\)行中\([j-t,j+t]\)的最大值来求出来

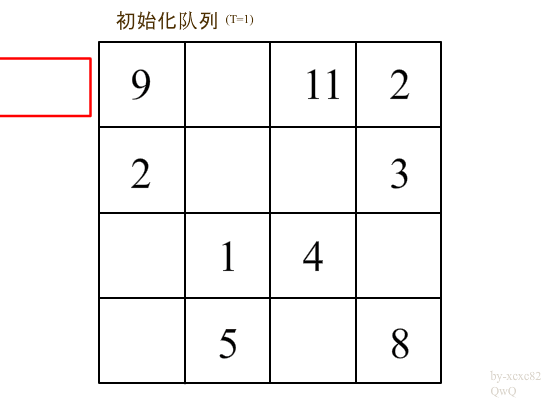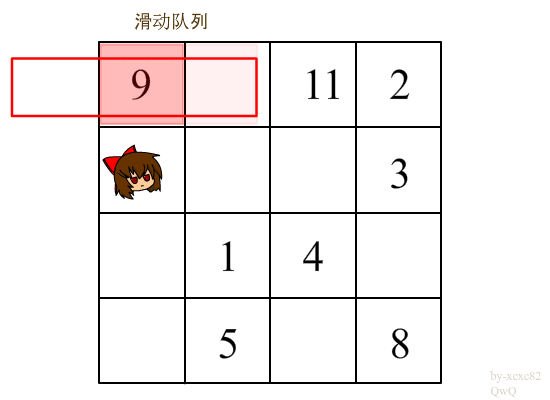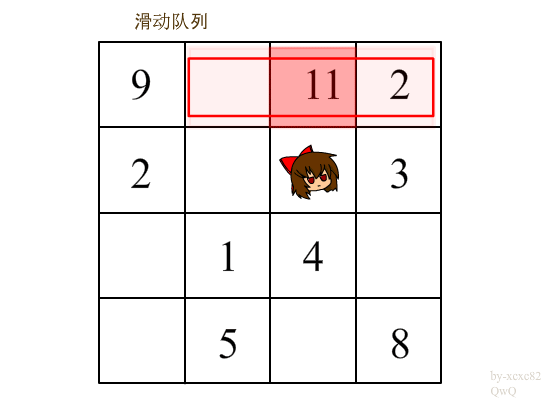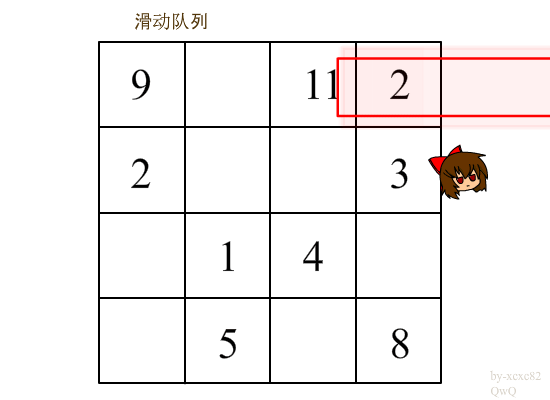
这里闲着无聊做了个\(gif\)

代码分析

开一个数组 \(q\) 模拟队列,用来滑动求最值

首先初始化第一行的\(dp[i][j]\)

第2~n行则利用\(q\)来求上一行的最大值进行转移

• swp函数

实现队列初始化功能

将前 \(t\) 个数加入队列

• swi函数

当插入新元素时

先判断队列是否在\([1,m]\)的区间内(不判会RE)

如果在区间内:

\(1\).调整队列单调性

\(2\).入队

反之,超出范围,不入队

\(3\).去掉"超时"元素

贴上丑陋的代码:

#include<bits/stdc++.h>
using namespace std;
#define MAXN 4010
int tail=0,head=1;
int n,m,k,t,ans; 
int q[MAXN],a[MAXN][MAXN],dp[MAXN][MAXN];
void queue_empty(){//清空窗口 
	tail=0,head=1;
}
void swi(int x,int last){//插入元素
   if(x+t<=m){//判断是否超过边界,不加会RE 
   	while(dp[last][x+t]>dp[last][q[tail]]&&tail>=head){//单调队列 
		tail--;
	}
	   
	q[++tail]=x+t;
   }
	
	while(q[head]+t<x) head++;	
}
void swp(int last){//初始化窗口 
	for(int i=1;i<=t;i++){
		while(dp[last][i]>dp[last][q[tail]]&&tail>=head){
		tail--;
	}
	  
	q[++tail] = i;
	}
}
int main(){

	scanf("%d%d%d%d",&n,&m,&k,&t);
	for (int i = 1; i <= k; i++) {
		int x, y, z;
		scanf("%d%d%d",&x,&y,&z);
		a[x][y] = z;
	}
   for(int i=1;i<=n;i++){//第一行初始化
   	dp[1][i]=a[1][i];
   }
   
   for(int i=2;i<=n;i++){
   	swp(i-1);
   	for(int j=1;j<=m;j++){
   		
   			swi(j,i-1);
   			
		  dp[i][j]=dp[i-1][q[head]]+a[i][j]; 
		  
	   }
	   queue_empty();
   }
   for(int i=1;i<=m;i++){
		ans=max(dp[n][i],ans);
	}
	cout<<ans;
}

如有错误欢迎dalao们指出qwq