hihoCoder #1151 : 骨牌覆盖问题·二 （矩阵快速幂，DP）

 

 

题意：给一个3*n的矩阵，要求用1*2的骨牌来填满，有多少种方案？

 

思路：

　　官网题解用的仍然是矩阵快速幂的方式。复杂度O(logn*8³)。

　　这样做需要构造一个2³*2³的矩阵，这个矩阵自乘n-1次，再来乘以初始矩阵init{0,0,0,0,0,0,0,1}后，变成矩阵ans{x,x,x,x,x,x,x,y}，y就是答案了，而x不必管。

　　主要在这个矩阵的构造，假设棋盘是放竖直的（即n*3），那么考虑在第i行进行填放，需要考虑到第i-1行的所有可能的状态（注意i-2行必须是已经填满了，否则第i行无法填到i-2行去）。放的时候有个规则，就是所放的每块1*2的骨牌，必须放有一半以上是在第i行的，而且不允许放到第i+1行去。其实就是根据3种选择来考虑变换，（1）不放（2）放横（3）放竖。

 

　　下图假设即将填第i+1行。

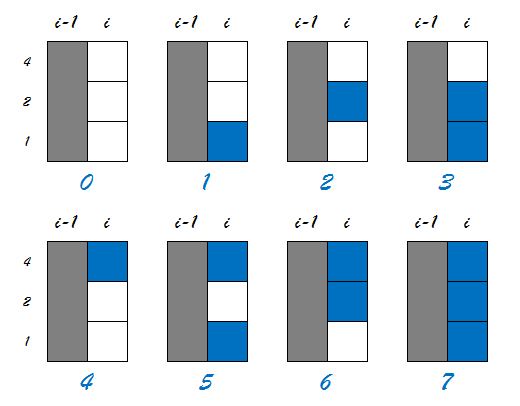
　　上图的编号代表了第i行的状态。

 

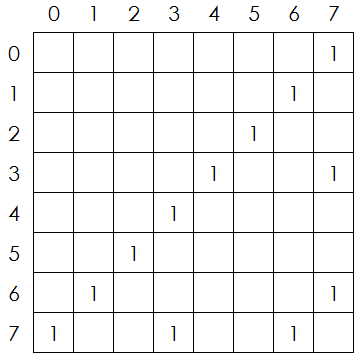
　　上图就是从第i行可以转移到第i+1行的状态。matrix[i][j]表示第i行的状态i转移到第i+1行的状态j的方案数，空格为0。

　　举个例子：第i行的状态为3，那么它只放一块骨牌时（即填满右上角的一个空格），转为4。如果放两块（即在4的基础上再放一块横的），就转为7。

 

　　上面只需要特别注意所假设的东西，而且要按照规则来放才行。

 

 

 　　2ms

#include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstring>
#define pii pair<int,int>
#define INF 0x3f3f3f3f
#define LL long long
using namespace std;
const int N=1e5+2;
const int mod=12357;
int M[8][8]={0,0,0,0,0,0,0,1,
             0,0,0,0,0,0,1,0,
             0,0,0,0,0,1,0,0,
             0,0,0,0,1,0,0,1,
             0,0,0,1,0,0,0,0,
             0,0,1,0,0,0,0,0,
             0,1,0,0,0,0,0,1,
             1,0,0,1,0,0,1,0};  //初始矩阵M

int init[8]={0,0,0,0,0,0,0,1};  //初始状态
int tot[8][8], cur[8][8], grid[8][8];   //临时的矩阵

void mul(int A[][8],int B[][8]) //处理两个8*8的矩阵相乘，并保存到A中
{
    for(int i=0; i<8; i++)
    {
        for(int j=0; j<8; j++)
        {
            int tmp=0;
            for(int k=0; k<8; k++)
            {
                tmp+=A[i][k]*B[k][j];
                tmp%=mod;
            }
            grid[i][j]=tmp;
        }
    }
    memcpy(A, grid, sizeof(grid));
}


int cal(int n)
{
    memcpy(tot, M, sizeof(M));
    memcpy(cur, M, sizeof(M));
    n--;    //tot已经是2^0了，所以自减1.
    while(n)
    {
        if(n&1==1)    mul(tot, cur);   //末位为1时，累乘到tot中
        mul(cur, cur);                 //翻倍
        n>>=1;
    }
    return tot[7][7];
}

int main()
{
    freopen("input.txt", "r", stdin);
    int n;
    while(~scanf("%d",&n))    printf("%d\n", cal(n));
    return 0;
}

 

 

 

 

　　还有一种方案仅需0ms。即递推，这个需要研究一下递推式，考虑各种情况的变化。不写了。