hihoCoder #1143 : 骨牌覆盖问题·一 (斐波那契数列)
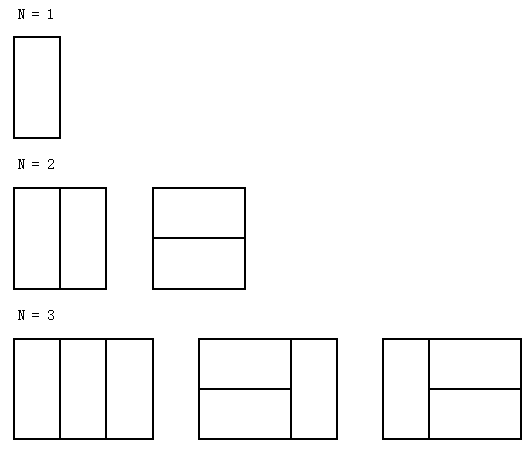
题意:我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢?
思路:这是斐波那契数列啊,f[n] = f[n-1] + f[n-2],初始时 f[0]=1,f[1]=1,f[2]=2。其实跟下面的递推思路差不多吧。但是关于这种简单,一般都可以用矩阵快速幂解决,即O(logn)时间内解决。主要难点是构造初始矩阵,如果是后面一个数字是由卡面两个数字相加而成的,那么一般可构造一个2*2的01矩阵,才这么小,随便试试吧,只要乘完的结果第二位是答案即可。

1 #include <iostream> 2 using namespace std; 3 const int yu = 19999997; 4 const int MASK = 1; 5 struct fuf 6 { 7 long long a,b, //矩阵如左 8 c,d; 9 }q[33]; 10 11 int handle_it() 12 { 13 q[0].a=0; q[0].b=1; q[0].c=1; q[0].d=1; //矩阵M的1次方 14 int i=1; 15 for(; i<=32; i++) //作乘 16 { 17 q[i].a = ( q[i-1].a * q[i-1].a + q[i-1].b * q[i-1].c )%yu; 18 q[i].b = ( q[i-1].a * q[i-1].b + q[i-1].b * q[i-1].d )%yu; 19 q[i].c = ( q[i-1].c * q[i-1].a + q[i-1].d * q[i-1].c )%yu; 20 q[i].d = ( q[i-1].c * q[i-1].b + q[i-1].d * q[i-1].d )%yu; 21 } 22 return 0; 23 } 24 int main() 25 { 26 handle_it(); 27 int n; 28 while( cin>>n ) 29 { 30 if( n>0 && n<=3) {cout<<n<<endl;continue;} 31 int i=0; 32 while( (n&MASK)==0 ) //直到n后面的0被去掉 33 { 34 i++; 35 n >>= 1; 36 } 37 fuf ans = q[i++]; 38 n >>= 1; 39 for( ; i<32 && n!=0; i++,n >>= 1) 40 { 41 if( (n&1)==1 ) 42 { 43 fuf tmp; 44 tmp.a = ( ans.a * q[i].a + ans.b * q[i].c )%yu; 45 tmp.b = ( ans.a * q[i].b + ans.b * q[i].d )%yu; 46 tmp.c = ( ans.c * q[i].a + ans.d * q[i].c )%yu; 47 tmp.d = ( ans.c * q[i].b + ans.d * q[i].d )%yu; 48 ans = tmp; 49 } 50 } 51 cout<<ans.d<<endl; 52 } 53 return 0; 54 }
写了个递推的思路:
(1)设dp[i]表示2*(i-1)的棋盘的摆放种数。
(2)假设第i列是放一个竖的,那么dp[i+1]+=dp[i]。这样只是一种,所以只是单纯用加的方式。
(3)假设第i列是放横的,那么连同第i+1列都被占用了,所以第i和i+1列就被摆放了两个横的,那么dp[i+2]+=dp[i]。这又是一种。
(4)2*n的棋盘答案就自然是dp[n+1]了,表示前n列的摆放种数。

1 #include <bits/stdc++.h> 2 #define pii pair<int,int> 3 #define INF 0x3f3f3f3f 4 #define LL long long 5 using namespace std; 6 const int N=1e8+2; 7 const int mod=19999997; 8 int dp[N], ans[N]; 9 void pre_cal() 10 { 11 dp[1]=1; 12 for(int i=1; i<N; i++) 13 { 14 dp[i+2]=(dp[i+2]+dp[i])%mod; //考虑放横 15 dp[i+1]=(dp[i+1]+dp[i])%mod; //考虑放直 16 ans[i]=(dp[i]+dp[i-1])%mod; 17 } 18 } 19 20 int main() 21 { 22 freopen("input.txt", "r", stdin); 23 pre_cal(); 24 int n; 25 while(~scanf("%d",&n)) printf("%d\n",ans[n]); 26 return 0; 27 }



